Cho hình bình hành ABCD, AB = 2AD. Gọi P, Q lần lượt là trung điểm của AB và CD.
a) Tứ giác APQD là hình gì? Vì sao?
b) Gọi I là giao điểm AQ và PD, gọi K là giao điểm của BQ và CP. Chứng minh tứ giác IPKQ là hình chữ nhật.
Giải bởi Vietjack
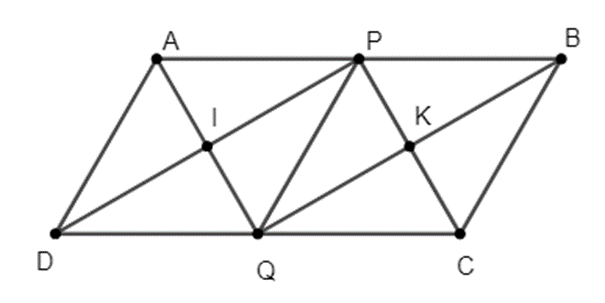
a) Xét tứ giác APQD có: AP // QD; AP = QD
Suy ra tứ giác APQD là hình bình hành
Mà AP = AD nên APQD là hình thoi
b) Xét tứ giác PBQD có: PB // QD; PB = QD
Suy ra tứ giác PBQD là hình bình hành
Do đó PD // QB và PD = QB (1)
Xét tứ giác BPQC có: BP // QC; BP = QC
Suy ra tứ giác BPQC là hình bình hành
Mà BP = BC nên BPQC là hình thoi
Nên PC và QB cắt nhau tại trung điểm của mỗi đường.
Hay K là trung điểm của BQ.
Do đó \(KQ = \frac{{BQ}}{2}\) (2)
Ta có: APQD là hình thoi
Nên AQ và PD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra I là trung điểm của PD
Do đó \(IP = \frac{{PD}}{2}\) (3)
Từ (1), (2) và (3) suy ra IP // QK và IP = QK.
Hay IPKQ là hình bình hành.
Mà \(\widehat {PIQ} = 90^\circ \) nên IPKQ là hình chữ nhật.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một nhóm học sinh có 6 bạn nam và 5 bạn nữ có bao nhiêu cách chọn ra 5 bạn trong đó có cả nam và nữ?
Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Vẽ tiếp tuyến AB; AC với (O) (B, C là tiếp điểm).
a) Chứng minh tam giác ABC đều.
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm O . Gọi M là trung điểm của BC; N, P lần lượt là chân đường cao kẻ từ B và C. Đường tròn đi qua 3 điểm M,N,P có phương trình: (T) \({\left( {x - 1} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = \frac{{25}}{4}\). Tìm phương trình đường tròn ngoại tiếp tam giác ABC.
Cho hình bình hành ABCD, có AC là đường chéo lớn. Kẻ CE vuông góc với AB tại E, BI vuông góc với AC tại I.
Chứng minh rằng:
Trong hệ tọa độ Oxy cho tam giác ABC có B(9; 7), C(11; −1). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ vectơ MN.
Cho tam giác DEF vuông ở E. Tia phân giác của góc D (M thuộc EF). Từ M vẽ MH vuông góc với DF (H thuộc DF).
a) Chứng minh: ∆DEM = ∆DHM.
b) Gọi K là giao điểm của tia DE và tia MH. Tam giác KMF là tam giác gì? Vì sao?
Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C.
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D). So sánh \(\widehat {CAD}\) và \(\widehat {CBD}\).
Cho tam giác ABC vuông tại A, đường cao AH, I là trung điểm của AB, lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D.
a) Tứ giác AKHD là hình gì?
b) Chứng minhAHBD là hình chữ nhật.
Cho ∆ABC có 3 góc nhọn, AH là đường cao. Vẽ HE vuông góc với AB tại E, HF vuông góc AC tại F .
a) Chứng minh: AE.AB = AF.AC.
b) Cho BH = 3cm, AH = 4cm. Tính AE, BE.
Chứng minh rằng n4 + 2n3 – n2 – 2n chia hết cho 24 với mọi số nguyên n.
Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKMB là hình gì?
Cho tam giác ABC, I là một điểm trong tam giác, IA, IB, IC theo thứ tự cắt BC, CA, AB ở M, N, P. Chứng minh rằng: \(\frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{IA}}{{IM}}\).
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F.
Chứng minh rằng: , AH² = AE.AB.
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D).
a) Chứng minh tứ giác AMBO nội tiếp.
b) Chứng minh MA2 = MC.MD.
