Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 77)
-
1326 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Thu gọn biểu thức sau:
A = 1 – 3 + 32 – 33 + … + 32021 – 32022
 Xem đáp án
Xem đáp án
Ta có: A = 1 – 3 + 32 – 33 + … + 32021 – 32022
3A = 3 – 32 + 33 – 34 + … + 32022 – 32023
⇒ 3A + A = (3 – 32 + 33 – 34 + … + 32022 – 32023) + (1 – 3 + 32 – 33 + … + 32021 – 32022)
⇔ 4A = 1 – 32023
\( \Leftrightarrow A = \frac{{1 - {3^{2023}}}}{4}\)
Vậy \(A = \frac{{1 - {3^{2023}}}}{4}\).
Câu 2:
Tính giá trị của biểu thức: P = 1 + 2 + 22 + 23 + 24 + … + 22020.
 Xem đáp án
Xem đáp án
Ta có: 2P = 2 + 22 + 23 + 24 + … + 22020 + 22021
⇒ 2P – P = (2 + 22 + 23 + 24 + … + 22020 + 22021) – (1 + 2 + 22 + 23 + 24 + … + 22020)
⇔ P = 22021 – 1
Vậy P = 22021 – 1.
Câu 3:
 Xem đáp án
Xem đáp án
Ta có: x ∈ {13; 14; 15 ....; 89; 90}.
Số số hạng là: (90 – 13) + 1 = 78 (số)
Tổng của các số tự nhiên x là:
(90 + 13) . 78 : 2 = 4017
Vậy tổng của các số tự nhiên x là 4017.
Câu 4:
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F.
Chứng minh rằng: , AH² = AE.AB.
 Xem đáp án
Xem đáp án
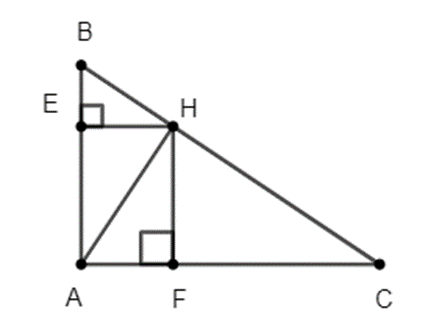
Xét ∆AEH và ∆AHB có:
\(\widehat {AEH} = \widehat {AHB} = 90^\circ \)
\(\widehat {BAH}\) chung
Do đó (g.g)
Suy ra \(\frac{{AE}}{{AH}} = \frac{{AH}}{{AB}} \Leftrightarrow A{H^2} = AE.AB\) (đpcm)
Câu 5:
Cho ∆ABC có 3 góc nhọn, AH là đường cao. Vẽ HE vuông góc với AB tại E, HF vuông góc AC tại F .
a) Chứng minh: AE.AB = AF.AC.
b) Cho BH = 3cm, AH = 4cm. Tính AE, BE.
 Xem đáp án
Xem đáp án
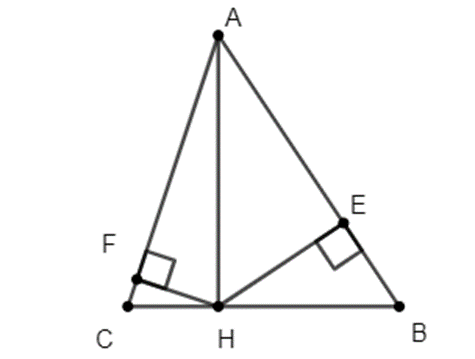
a) Xét ΔAHB vuông tại H, HE là đường cao nên ta có AH² = AE.AB
Xét ΔAHC vuông tại H, HF là đường cao nên ta có AH² = AF.AC
⇒ AE.AB = AF.AC
b) Xét ΔAHB vuông tại H. Áp dụng định lý Py-ta-go:
AB² = AH² + BH² = 16 + 9 = 25
⇒ AB = 5 (cm)
Có AH² = AE.AB ⇒ AE = 3,2 (cm)
Có BE = AB – AE = 5 – 3,2 = 1,8 (cm)
Câu 6:
Chứng minh rằng n4 + 2n3 – n2 – 2n chia hết cho 24 với mọi số nguyên n.
 Xem đáp án
Xem đáp án
Ta có: n4 + 2n3 – n2 – 2n
= (n4 + 2n3) – (n2 + 2n)
= n3(n + 2) – n(n + 2)
= (n3 – n)(n + 2)
= n(n2 – 1)(n + 2)
= (n – 1)n(n + 1)(n + 2)
Ta thấy (n – 1)n(n + 1)(n + 2) là tích bốn số nguyên liên tiếp nên sẽ chứa một số chia hết cho 2 và một số chia hết cho 4, từ đó suy ra tích bốn số nguyên liên tiếp chia hết cho 8.
Đồng thời, trong bốn số nguyên liên tiếp luôn chứa tích của ba số nguyên liên tiếp, đồng nghĩa với việc tích bốn số nguyên liên tiếp chia hết cho 3.
Mà 24 = 3.8
Vì vậy tích bốn số nguyên liên tiếp chia hết cho 3.8 = 24.
Vậy n4 + 2n3 – n2 – 2n chia hết cho 24 với mọi số nguyên n.
Câu 7:
Có bao nhiêu số nguyên dương không vượt quá 1000 mà chia hết cho 3 hoặc chia hết cho 5?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
• Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇔ 0 < a < 333,3
Mà a nguyên nên có 333 số thỏa mãn.
• Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇔ 0 < b ≤ 200
Nên có 200 số thỏa mãn.
• Số chia hết cho cả 3 và 5 có dạng 15c ta có 0 < 15c ≤ 1000 ⇔ 0 < c < 66,6
Nên có 66 số thỏa mãn.
Do đó số các số thỏa mãn đề bài là: 333 + 200 – 66 = 467.
Câu 8:
Có bao nhiêu số nguyên dương không lớn hơn 2020 mà chia hết cho 2 hoặc cho 3?
 Xem đáp án
Xem đáp án
Số các số chia hết cho 2 là: \(\frac{{2020 - 2}}{2} + 1 = 1010\).
Số các số chia hết cho 3 là: \(\frac{{2019 - 3}}{3} + 1 = 673\).
Số các số chia hết cho cả 2 và 3 (hay là chia hết cho 6) là:
\(\frac{{2016 - 6}}{6} + 1 = 336\).
Vậy có tất cả số là: 1010 + 673 – 336 = 1347.
Câu 9:
Cho a, b > 0 và a + b = 4. Tìm GTLN của \(P = \left( {1 - \frac{1}{a}} \right)\left( {1 - \frac{1}{b}} \right)\).
 Xem đáp án
Xem đáp án
Do a, b > 0 nên \(1 - \frac{1}{a} > 0\); \(1 - \frac{1}{b} > 0\)
Áp dụng BĐT:
\(xy \le \frac{{{{\left( {x + y} \right)}^2}}}{4} \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy \Leftrightarrow {(x - y)^2} \ge 0\) (luôn đúng)
\(P = \left( {1 - \frac{1}{a}} \right)\left( {1 - \frac{1}{b}} \right)\) \( \le \frac{1}{4}{\left( {1 - \frac{1}{a} + 1 - \frac{1}{b}} \right)^2} = \frac{1}{4}{\left[ {2 - \left( {\frac{1}{a} + \frac{1}{b}} \right)} \right]^2}\)
Chứng minh BĐT \(\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\) (1)
\(\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\)
\( \Leftrightarrow \left( {\frac{{x + y}}{{xy}}} \right)\left( {x + y} \right) \ge 4\)
⇔ (x + y)2 ≥ 4xy
⇔ (x – y)2 ≥ 0 (luôn đúng)
Khi đó: \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}} = \frac{4}{4} = 1\)
⇒ \(2 - \left( {\frac{1}{a} + \frac{1}{b}} \right) \le 2 - 1 = 1\)
\( \Rightarrow \frac{1}{4}{\left[ {2 - \left( {\frac{1}{a} + \frac{1}{b}} \right)} \right]^2} \le \frac{1}{4}.1 = \frac{1}{4}\)
Vậy \({P_{\max }} = \frac{1}{4}\) khi a = b = 2.
Câu 10:
Từ một hộp chứa 6 quả cầu trắng và 4 quả cầu đen, lấy ra ngẫu nhiên cùng một lúc 4 quả. Xác suất để lấy ra được 4 quả cùng màu là bao nhiêu?
 Xem đáp án
Xem đáp án
Không gian mẫu Ω là: \(\Omega = C_{10}^4 = 210\).
Gọi A là biến cố chọn được 4 quả cùng màu. 4 quả cùng màu có thể là 4 quả cùng màu trắng hoặc 4 quả cùng màu đen.
Ta có: \(A = C_6^4 + C_4^4 = 15 + 1 = 16\).
Vậy \(P(A) = \frac{A}{\Omega } = \frac{{16}}{{210}} = \frac{8}{{105}}\).
Câu 11:
Từ một hộp chứa 6 quả cầu trắng và 4 quả cầu đen, lấy ra ngẫu nhiên cùng một lúc 4 quả. Xác suất để lấy ra có ít nhất 1 quả cầu màu trắng là bao nhiêu?
 Xem đáp án
Xem đáp án
Không gian mẫu Ω là: \(\Omega = C_{10}^4 = 210\).
Gọi A là biến cố chọn được 4 quả có ít nhất 1 quả cầu màu trắng.
Suy ra \(\overline A \) là biến cố chọn được 4 quả không có quả nào màu trắng.
Khi đó ta có: \(\overline A = C_4^4 = 1\).
Khi đó: \(P(\overline A ) = \frac{1}{{210}} \Rightarrow P\left( A \right) = 1 - \frac{1}{{210}} = \frac{{209}}{{210}}\).
Vây xác suất cần tìm là \(\frac{{209}}{{210}}\).
Câu 12:
Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Vẽ tiếp tuyến AB; AC với (O) (B, C là tiếp điểm).
a) Chứng minh tam giác ABC đều.
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi.
 Xem đáp án
Xem đáp án
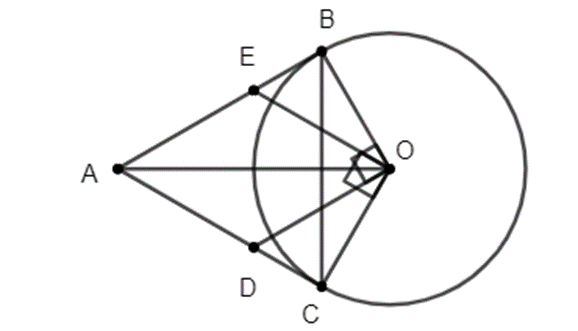
a) Ta có ∆AOC vuông tại C
\(\sin \widehat {CAO} = \frac{{OC}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2} \Rightarrow \widehat {CAO} = 30^\circ \)
Mà A là giao điểm của 2 tiếp tuyến của (O).
\( \Rightarrow \widehat {BAC} = 2.\widehat {OAC} = 2.30^\circ = 60^\circ \) (1)
Và BA = AC (2)
Từ (1) và (2) nên ta có: ∆ABC đều.
b) Ta có: OD⊥OB; AB⊥OB
Suy ra OD // AB hay OD // AE (3)
Chứng minh tương tự: OE / /AD (4)
Từ (3), (4) suy ra ADOE là hình bình hành.
Ta có ∆AOC vuông tại C nên \(\widehat {OAB} + \widehat {AOB} = 90^\circ \)
\( \Rightarrow \widehat {AOB} = 90^\circ - \widehat {OAB} = 90^\circ - 30^\circ = 60^\circ \)
Ta lại có \(\widehat {DOB} = 90^\circ \Rightarrow \widehat {DOA} + \widehat {AOB} = 90^\circ \)
\( \Leftrightarrow \widehat {DOA} + 60^\circ = 90^\circ \Leftrightarrow \widehat {DOA} = 30^\circ \)
\( \Rightarrow \widehat {OAD} = \widehat {DOA} = 30^\circ \)
⇒ ∆DOA cân tại D
⇒ AD = DO.
Mà ADOE là hình bình hành nên ADOE là hình thoi.
Câu 13:
Cho hình chóp S ABCD có đáy ABCD là hình bình hành với O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm SA và SD. Chứng minh ba đường thẳng SO, BN, CM đồng quy.
 Xem đáp án
Xem đáp án
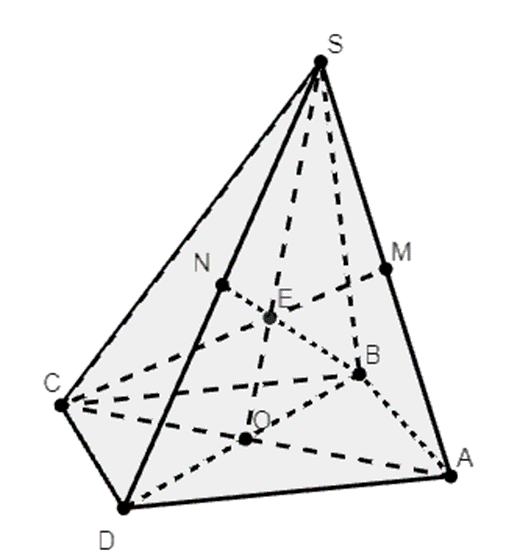
Gọi E = BN ∩ CM ta có: \[\left\{ \begin{array}{l}E \in BN \subset \left( {SBD} \right)\\E \in CM \subset \left( {SAC} \right)\end{array} \right.\]
⇒ E ∈ (SAC) ∩ (SBD) (1)
Xét (SAC) và (SBD) có:
+) S là điểm chung thứ nhất.
+) O = AC ∩ BD \( \Rightarrow \left\{ \begin{array}{l}O \in AC \subset (SAC)\\O \in BD \subset (SBD)\end{array} \right.\)
⇒ O ∈ (SAC) ∩ (SBD) ⇒ O là điểm chung thứ hai.
⇒ (SAB) ∩ (SCD) = SO (2)
Từ (1) và (2) suy ra E ∈ SO.
Hay ba đường thẳng SO, BN, CM đồng quy tại E.
Câu 14:
Cho tam giác ABC có \(\widehat A = 90^\circ \), AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K.
Chứng minh rằng: AK = AD.
 Xem đáp án
Xem đáp án
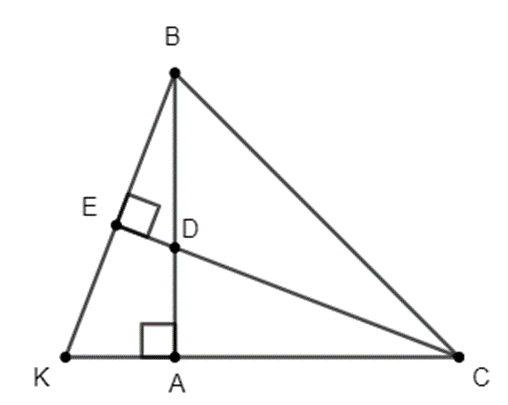
Xét ∆AKB và ∆ADC có:
\(\widehat {BAK} = \widehat {DAC} = 90^\circ \)
AB = AC (gt)
\(\widehat {ABK} = \widehat {ACD}\) (cùng phụ với \(\widehat K\))
⇒ ∆AKB = ∆ADC (g.c.g)
⇒ AK = AD (đpcm)
Câu 15:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK.
 Xem đáp án
Xem đáp án
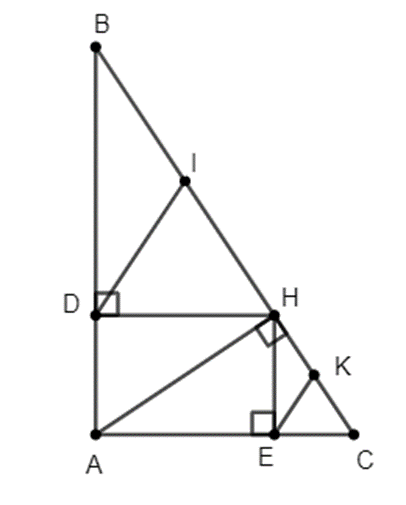
• Xét ∆BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
Nên DI = IB = \(\frac{1}{2}BH\) (tính chất tam giác vuông)
Suy ra ΔIDB cân tại I.
Do đó \(\widehat {DIB} = 180^\circ - 2\widehat B\) (1)
• Xét ∆HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
Nên EK = KH = \(\frac{1}{2}HC\) (tính chất tam giác vuông)
Suy ra ΔKHE cân tại K.
Do đó \(\widehat {EKH} = 180^\circ - 2\widehat {KHE}\) (2)
Tứ giác ADHE là hình chữ nhật nên: HE // AD hay HE // AB.
Do đó \(\widehat B = \widehat {KHE}\) (đồng vị)
Từ (1), (2) và (3) suy ra: \(\widehat {DIB} = \widehat {EKH}\) (3)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
Câu 16:
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D).
a) Chứng minh tứ giác AMBO nội tiếp.
b) Chứng minh MA2 = MC.MD.
 Xem đáp án
Xem đáp án
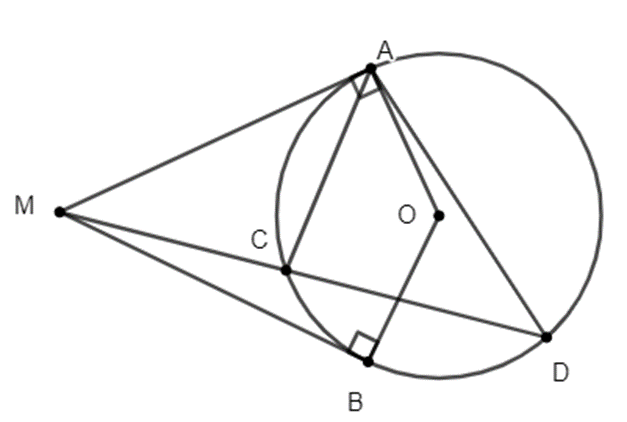
a) Xét tứ giác AOBM với \(\widehat {MAO}\) và \(\widehat {MBO}\) có:
\(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \)
Do đó AOBM là tứ giác nội tiếp đường tròn.
b) Xét ∆MCA và ∆MAD có:
\(\widehat {MAC} = \widehat {MDA}\) (góc tạo bới tia tiếp tuyến và dây cung, góc nội tiếp đường tròn cùng chắn cung AC)
\(\widehat M\) là góc chung
Do đó (g.g)
Suy ra \(\frac{{MC}}{{MA}} = \frac{{MA}}{{MD}}\).
Vậy MA2 = MC.MD (đpcm)
Câu 17:
Chứng minh với a, b, c ≥ 1 ta có: \[\frac{1}{{{a^3} + 1}} + \frac{1}{{{b^3} + 1}} + \frac{1}{{{c^3} + 1}} \ge \frac{3}{{1 + abc}}\].
 Xem đáp án
Xem đáp án
Ta cần chứng minh BĐT phụ:
\(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\) với a, b > 0, ab ≥ 1
\( \Leftrightarrow \left( {\frac{1}{{1 + {a^2}}} - \frac{1}{{1 + ab}}} \right) + \left( {\frac{1}{{1 + {b^2}}} - \frac{1}{{1 + ab}}} \right) \ge 0\)
\( \Leftrightarrow \frac{{ab - {a^2}}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)}} + \frac{{ab - {b^2}}}{{\left( {1 + {b^2}} \right)\left( {1 + ab} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {ab - {a^2}} \right)\left( {1 + {b^2}} \right) + \left( {ab - {b^2}} \right)\left( {1 + {a^2}} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{{{\left( {a - b} \right)}^2}\left( {ab - 1} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)}} \ge 0\) luôn đúng với \(\forall \)a,b > 0, ab ≥ 1
Ta có: \[\frac{1}{{{a^3} + 1}} + \frac{1}{{{b^3} + 1}} + \frac{1}{{{c^3} + 1}} \ge \frac{3}{{1 + abc}}\]
\( \Leftrightarrow \frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{4}{{1 + abc}}\)
Áp dụng ĐBT trên ta có:
\(VT = \frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{2}{{1 + \sqrt {{a^3}{b^3}} }} + \frac{2}{{1 + \sqrt {ab{c^4}} }}\)
\(VT \ge \frac{4}{{1 + \sqrt {\sqrt {{a^3}{b^3}.ab{c^4}} } }} = \frac{4}{{1 + abc}}\)
Vậy \[\frac{1}{{{a^3} + 1}} + \frac{1}{{{b^3} + 1}} + \frac{1}{{{c^3} + 1}} \ge \frac{3}{{1 + abc}}\] (đpcm).
Câu 18:
Tìm số \(\overline {ab} \) biết \(\overline {ab} \) + a + b = 95.
 Xem đáp án
Xem đáp án
Ta có: \(\overline {ab} \) + a + b = 95
⇔ a ´ 10 + b + a + b = 95
⇔ 11a + 2b = 95
⇔ aa + 2b = 95
Vì 95 là số lẻ , 2b là số chẵn nên aa là số lẻ.
Khi đó ta có: aa = {11; 33; 55; 77}
Để b là số có 1 chữ số thì 2b cao nhất là: 9 ´ 2 = 18
Ta có:
2b = 95 – 11 = 84 (loại)
2b = 95 – 33 = 62 (loại)
2b = 95 – 55 = 40 (loại)
2b = 95 – 77 = 18 (thỏa mãn)
Vậy số cần tìm là 79.
Câu 19:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây là sai?
A. Đường thẳng IO song song với mặt phẳng (SAD);
B. Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác;
C. Đường thẳng IO song song với mặt phẳng (SAB);
D. Giao tuyến của hai mặt phẳng (IBD) và (SAC) là IO.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
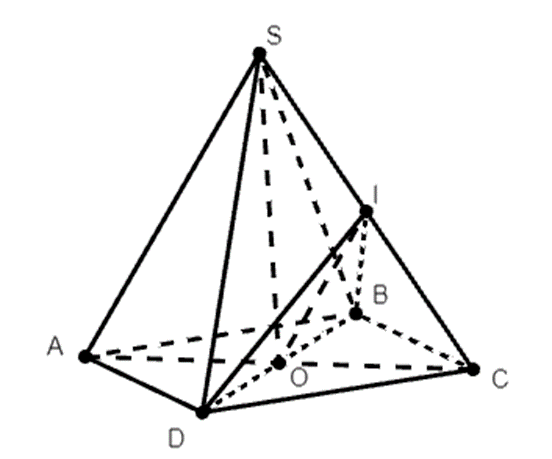
Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.
Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.
Câu B ta có thiết diện là ∆IBD nên B sai.
Câu 20:
Cho tam giác ABC. Tập hợp các điểm M sao cho
\(\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right)\left( {\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right) = 0\) là một đường tròn.
 Xem đáp án
Xem đáp án
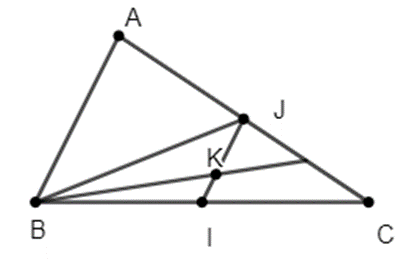
Gọi I, J lần lượt là trung điểm của BC, AC.
K là trọng tâm của tam giác JBC ta có:
\(\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right)\left( {\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right) = 0\)
\( \Leftrightarrow 2\overrightarrow {MI} \left[ {\left( {\overrightarrow {MA} + \overrightarrow {MC} } \right) + 2\overrightarrow {MB} + 2\overrightarrow {MC} } \right] = 0\)
\( \Leftrightarrow 2\overrightarrow {MI} \left( {2\overrightarrow {MJ} + 2\overrightarrow {MB} + 2\overrightarrow {MC} } \right) = 0\)
\( \Leftrightarrow 4\overrightarrow {MI} \left( {\overrightarrow {MJ} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\)
\( \Leftrightarrow 4\overrightarrow {MI} .3\overrightarrow {MK} = 0\)
\( \Leftrightarrow \overrightarrow {MI} .\overrightarrow {MK} = 0\)
⇒ MI⊥MK \( \Rightarrow \widehat {IMK} = 90^\circ \)
Do đó điểm M luôn nhìn đoạn IK một góc 90° hay tập hợp điểm M cần tìm là đường tròn đường kính IK.
Câu 21:
Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKCM là hình gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
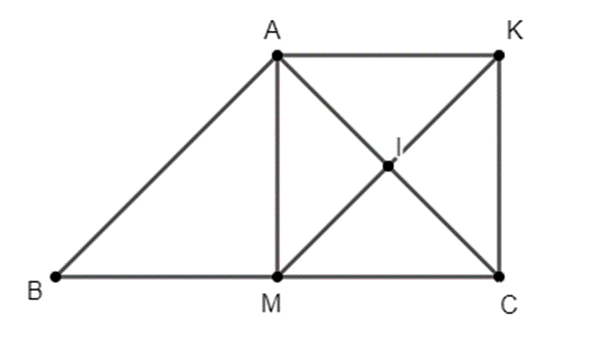
Xét tứ giác AKCM có:
AC∩MK = {I}
Mà I là chung điểm của hai đoạn AC và MK (gt)
⇒ Tứ giác AKCM là hình bình hành (1)
Vì ∆ABC cân tại A
⇒ AM vừa là đường trung tuyến và cũng là đường cao của ∆ABC.
\[ \Rightarrow \widehat {AMC} = 90^\circ \] (2)
Từ (1) và (2) suy ra tứ giác AKCM là hình chữ nhật.
Câu 22:
Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKMB là hình gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
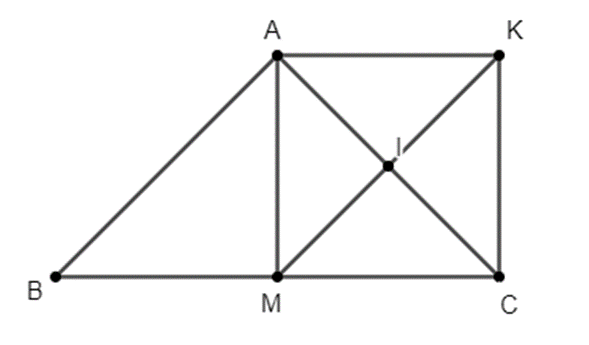
Tứ giác AKCM có hai đường chéo AC và MK cắt nhau tại trung điểm I của mỗi đường
Suy ra tứ giác AKCM là hình bình hành (1)
Xét ∆ABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao của ∆ABC hay \[\widehat {AMC} = 90^\circ \] (2)
Từ (1) và (2) suy ra tứ giác AKCM là hình chữ nhật.
Vì AKCM là hình chữ nhật nên ta có: AK // CM hay AK // BM và AK = CM.
Mà CM = BM (do M là trung điểm của BC)
Do đó AK = BM và AK // BM.
Từ đó suy ra tứ giác AKMB là hình bình hành.
Câu 23:
Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
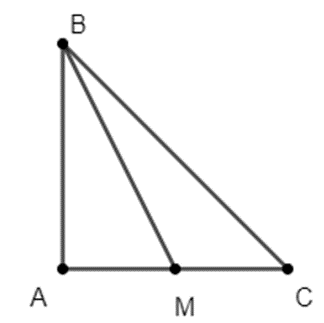
Gọi M là trung điểm của AC suy ra \(AM = \frac{{AC}}{2} = \frac{a}{2}\)
Do ∆BAM vuông tại A, áp dụng định lí Py-ta-go, ta có:
\(BM = \sqrt {A{B^2} + A{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}\)
Câu 24:
Cho tam giác ABC có AB = 2; AC = 3; \(\widehat A = 60^\circ \). Tính độ dài cạnh BC.
 Xem đáp án
Xem đáp án
Áp dụng định lý cosin, ta có:
BC2 = AB2 + AC2 – 2AB.AC.cos\(\widehat A\)
= 22 + 32 – 2.3.cos60° = 7
\( \Rightarrow BC = \sqrt 7 \)
Câu 25:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, E là điểm đối xứng với H qua AC.
a) Chứng minh D đối xứng với E qua A.
b) Tam giác DHE là tam giác gì? Vì sao?
c) Tứgiác BDEC là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
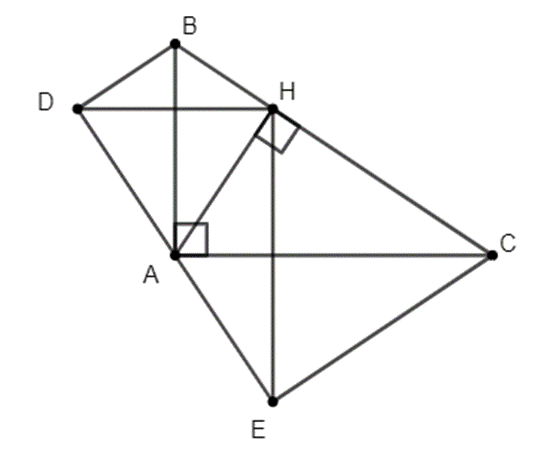
a) Vì D là điểm đối xứng với H qua AB nên AB là đường trung trực của DH suy ra AH = AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE suy ra AH = AE (2)
Từ (1) và (2) suy ra AD = AE (3)
Mặt khác \(\widehat {DAB} = \widehat {BAH}\); \(\widehat {HAC} = \widehat {CAE}\)
Và \(\widehat {BAH} + \widehat {HAC} = 90^\circ \)
Do đó \(\widehat {DAB} + \widehat {BAH} + \widehat {HAC} + \widehat {CAE} = 180^\circ \)
Tức là D, A, E thẳng hành (4)
Từ (3) và (4) suy ra D và E đối xứng với nhau qua A.
b) ∆DHE có HA là trung điểm và \(HA = \frac{1}{2}DE\) nên ∆DHE vuông tại H.
c) Xét ∆ADB và ∆AHB có:
AD = AH
AB chung
DB = BH (D đối xứng với H qua AB)
Do đó ∆ADB = ∆AHB (c.c.c)
Suy ra \(\widehat {ADB} = \widehat {AHB} = 90^\circ \)
Tương tự ta có: ∆AHC = ∆AEC
Do đó \(\widehat {AEC} = \widehat {AHC} = 90^\circ \)
Suy ra BD // CE (cùng vuông góc với DE)
Nên tứ giác BAEC là hình thang có hai góc vuông kề cạnh bên DE nên BAEC là hình thang vuông.
Câu 26:
Cho tam giác ABC, I là một điểm trong tam giác, IA, IB, IC theo thứ tự cắt BC, CA, AB ở M, N, P. Chứng minh rằng: \(\frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{IA}}{{IM}}\).
 Xem đáp án
Xem đáp án
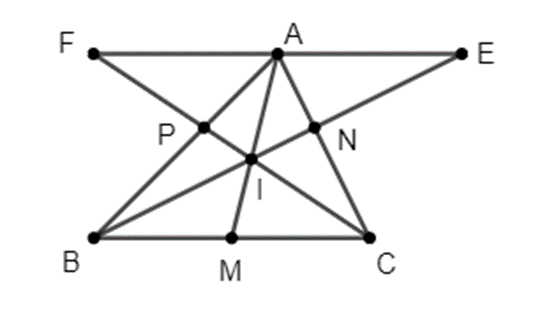
Qua A kẻ đường thắng song song với BC. Đường thẳng này cắt BN, CP lần lượt ở E và F.
Áp dụng hệ quả của định lý Ta-lét cho AE // BC và FA // BC, ta được:
\(\frac{{NA}}{{NC}} = \frac{{EA}}{{BC}}\) (1)
\(\frac{{PA}}{{PB}} = \frac{{AF}}{{BC}}\) (2)
Cộng theo vế các đẳng thức (1) và (2), ta được:
\(\frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{EF}}{{BC}} = \frac{{IA}}{{IM}}\)
\( \Rightarrow \frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{IA}}{{IM}}\) (đpcm)
Câu 27:
Cho tam giác DEF vuông ở E. Tia phân giác của góc D (M thuộc EF). Từ M vẽ MH vuông góc với DF (H thuộc DF).
a) Chứng minh: ∆DEM = ∆DHM.
b) Gọi K là giao điểm của tia DE và tia MH. Tam giác KMF là tam giác gì? Vì sao?
 Xem đáp án
Xem đáp án
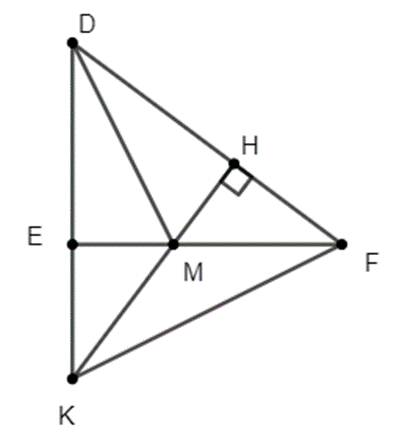
a) Xét ∆DEM và ∆DHM có:
\(\widehat E = \widehat H = 90^\circ \)
DM chung
\(\widehat {EDM} = \widehat {HDM}\) (gt)
Do đó ∆DEM = ∆DHM (g.c.g)
Suy ra EM = HM (hai cạnh tương ứng).
b) Xét ∆EMK và ∆HMF có:
\(\^E = \widehat H = 90^\circ \)
EM = MH
\(\widehat {EMK} = \widehat {HMF}\)
Do đó ∆EMK = ∆HMF (c.g.c)
Suy ra MK = MF (hai cạnh tương ứng).
Vậy tam giác MKF cân tại M.
Câu 28:
Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O, bán kính đáy r = 5. Một thiết diện qua đỉnh là tam giác SAB đều có cạnh bằng 8. Khoảng cách từ O đến mặt phẳng (SAB) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
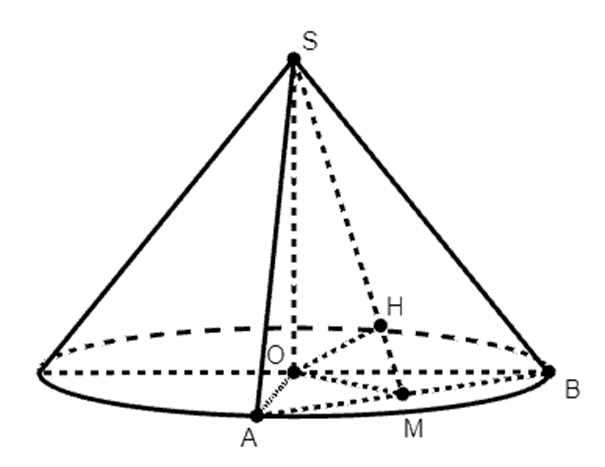
Ta có: \(\left\{ \begin{array}{l}OM = 3\\SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {39} \end{array} \right.\)
Gọi M là trung điểm của AB.
Ta có: \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot (SOM)\)
Dựng OH⊥SM ⇒ OH⊥(SAB)
Xét ∆SOM vuông tại O có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{S{O^2}}} = \frac{{16}}{{117}}\)
\( \Rightarrow OH = \frac{{3\sqrt {13} }}{4}\).
Câu 29:
Trong hệ tọa độ Oxy cho tam giác ABC có B(9; 7), C(11; −1). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ vectơ MN.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Gọi A(x; y). Khi đó:
• M là trung điểm AB nên \(M\left( {\frac{{x + 9}}{2};\frac{{7 + y}}{2}} \right)\)
• N là trung điểm của AC nên \(N\left( {\frac{{x + 11}}{2};\frac{{ - 1 + y}}{2}} \right)\)
Do đó \(MN\left( {\frac{{x + 11 - x - 9}}{2};\frac{{ - 1 + y - 7 - y}}{2}} \right)\) hay MN(1; −4).
Câu 30:
Cho hình bình hành ABCD, AB = 2AD. Gọi P, Q lần lượt là trung điểm của AB và CD.
a) Tứ giác APQD là hình gì? Vì sao?
b) Gọi I là giao điểm AQ và PD, gọi K là giao điểm của BQ và CP. Chứng minh tứ giác IPKQ là hình chữ nhật.
 Xem đáp án
Xem đáp án
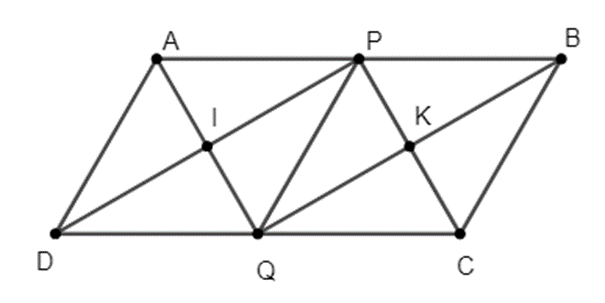
a) Xét tứ giác APQD có: AP // QD; AP = QD
Suy ra tứ giác APQD là hình bình hành
Mà AP = AD nên APQD là hình thoi
b) Xét tứ giác PBQD có: PB // QD; PB = QD
Suy ra tứ giác PBQD là hình bình hành
Do đó PD // QB và PD = QB (1)
Xét tứ giác BPQC có: BP // QC; BP = QC
Suy ra tứ giác BPQC là hình bình hành
Mà BP = BC nên BPQC là hình thoi
Nên PC và QB cắt nhau tại trung điểm của mỗi đường.
Hay K là trung điểm của BQ.
Do đó \(KQ = \frac{{BQ}}{2}\) (2)
Ta có: APQD là hình thoi
Nên AQ và PD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra I là trung điểm của PD
Do đó \(IP = \frac{{PD}}{2}\) (3)
Từ (1), (2) và (3) suy ra IP // QK và IP = QK.
Hay IPKQ là hình bình hành.
Mà \(\widehat {PIQ} = 90^\circ \) nên IPKQ là hình chữ nhật.
Câu 31:
Khi nhân một số với 205, do vô ý Tâm đã quên viết chữ số 0 của số 205 nên tích giảm đi 42 120 đơn vị. Tìm tích đúng của phép nhân đó.
 Xem đáp án
Xem đáp án
Số 205 mà bỏ chữ số 0 thì thành số 25. Như vậy Tâm đã viết nhầm làm giảm 1 thừa số đi số đơn vị là:
205 – 25 = 180 (đơn vị)
Do đó tích giảm đi 180 lần thừa số kia, mà tích giảm đi 42120 đơn vị nên thừa số kia là :
42 120 : 180 = 234
Tích đúng là:
234 ´ 205 = 47 970
Đáp số: 47 970.
Câu 32:
Một người nông dân mua một con bò giá 10 triệu, rồi bán đi với giá 15 triệu, sau đó mua lại giá 20 triệu rồi lại bán đi với giá 17 triệu. Người bán bò lãi bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Người bán hàng lãi số tiền là:
(15 – 10) – 20 + 17 = 2 (triệu đồng)
Đáp số: 2 triệu đồng.
Câu 33:
Một vòi nước chảy vào cái bể không có nước trong 2 giờ. Một giờ đầu vòi chảy được \[\frac{1}{4}\] bể, giờ sau chạy được \(\frac{1}{6}\) bể. Người ta đã dùng lượng nước bằng \(\frac{1}{3}\) bể. Hỏi lượng nước còn lại chiếm mấy phần bể nước?
 Xem đáp án
Xem đáp án
Cả 2 giờ vòi đó chảy được số phần bể là:
\(\frac{1}{4} + \frac{1}{6} = \frac{5}{{12}}\) (bể)
Lượng nước còn lại chiếm số phần bể là:
\(\frac{5}{{12}} - \frac{1}{3} = \frac{1}{{12}}\) (bể)
Đáp số: \(\frac{1}{{12}}\) bể.
Câu 34:
Cho biểu thức: \(A = \frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\) (x ∉ {0; 1; −1})
a) Rút gọn biểu thức.
b) Tìm x để biểu thức A = 2.
c) Tìm giá trị nguyên của x để giá trị của biểu thức là một số nguyên.
 Xem đáp án
Xem đáp án
Điều kiện x ≠ 0; x ≠ 1; x ≠ −1
a) Với x ≠ 0; x ≠ 1; x ≠ −1, ta có:
\(A = \frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\)
\( = \frac{{x({x^2} + 2x + 1)}}{{x\left( {{x^2} - 1} \right)}}\)
\( = \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{x + 1}}{{x - 1}}\)
b) Với x ≠ 0; x ≠ 1; x ≠ −1, ta có:
\(A = \frac{{x + 1}}{{x - 1}} = 2\)
⇔ x + 1 = 2x – 2
⇔ x = 3 (TMĐK)
Vậy với x = 3 thì A = 2.
c) \(A = \frac{{x + 1}}{{x - 1}} = \frac{{(x - 1) + 2}}{{x - 1}} = 1 + \frac{2}{{x - 1}}\)
Để A nguyên thì 2 \( \vdots \) (x – 1)
⇒ (x – 1) ∈ Ư(2)
Mà Ư(2) = {1; −1; 2; −2}
⇒ x ∈ {2; 0; 3; −1}
Kết hợp với điều kiện x ≠ 0; x ≠ 1; x ≠ −1 ta có: x ∈ {2; 3}.
Câu 35:
Cho: \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0\) (abc ≠ 0). Tính biểu thức: \(A = \frac{{b + c}}{a} + \frac{{c + a}}{b} + \frac{{a + b}}{c}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0\)
\( \Leftrightarrow \frac{{ab + bc + ca}}{{abc}} = 0\)
⇔ ab + bc + ca = 0
Mặt khác, \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0\)
\( \Leftrightarrow \frac{1}{a} + \frac{1}{b} = - \frac{1}{c}\)
\( \Leftrightarrow {\left( {\frac{1}{a} + \frac{1}{b}} \right)^3} = - \frac{1}{{{c^3}}}\)
\( \Leftrightarrow \frac{1}{{{a^3}}} + \frac{1}{{{b^3}}} + 3.\frac{1}{{ab}}.\left( {\frac{1}{a} + \frac{1}{b}} \right) = - \frac{1}{{{c^3}}}\)
\( \Leftrightarrow \frac{1}{{{a^3}}} + \frac{1}{{{b^3}}} + 3.\frac{1}{{ab}}.\left( { - \frac{1}{c}} \right) = \frac{{ - 1}}{{{c^3}}}\)
\( \Leftrightarrow \frac{1}{{{a^3}}} + \frac{1}{{{b^3}}} + \frac{1}{{{c^3}}} = \frac{3}{{abc}}\) (*)
Khi đó: \(\frac{{\left( {b + c} \right)}}{a} = \frac{{ab + ac}}{{{a^2}}} = \frac{{ - bc}}{{{a^2}}} = \frac{{ - abc}}{{{a^2}}}\)
Tương tự ta có: \(\frac{{\left( {a + b} \right)}}{c} = \frac{{ - abc}}{{{c^3}}}\); \(\frac{{\left( {a + c} \right)}}{{{b^2}}} = \frac{{ - abc}}{{{b^3}}}\).
\(M = \frac{{ - abc}}{{{a^3}}} + \frac{{ - abc}}{{{b^3}}} + \frac{{ - abc}}{{{c^3}}}\)
\( = - abc\left( {\frac{1}{{{a^3}}} + \frac{1}{{{b^3}}} + \frac{1}{{{c^3}}}} \right)\)
\( = - abc.\frac{3}{{abc}} = - 3\) (theo *)
Vậy M = −3.
Câu 36:
Cho tam giác ABC cân tại A có AB = 10 cm. Lấy điểm M trên đoạn AB sao cho AM = 4 cm, qua M kẻ đường thẳng d song song với BC cắt AC tại N. Tính tỉ số AN và AC?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
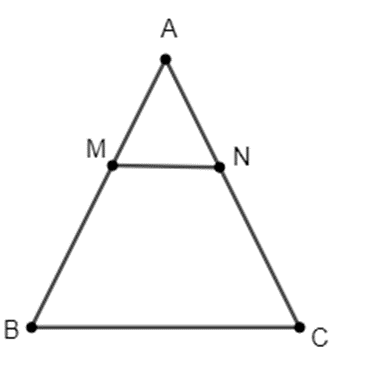
Vì ∆ABC cân tại A nên AB = AC = 10 cm.
Vì MN // BC, theo định lí Ta-lét, ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)
Mà AB = AC nên AM = AN = 4 cm.
Suy ra \(\frac{{AN}}{{AC}} = \frac{4}{{10}} = \frac{2}{5}\)
Câu 37:
Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C.
 Xem đáp án
Xem đáp án
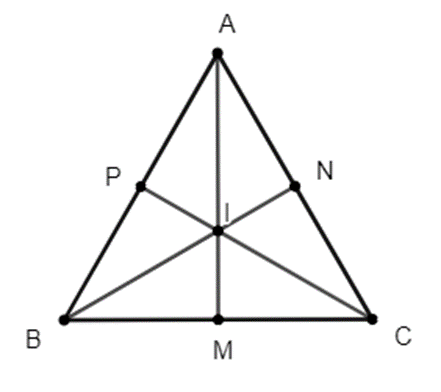
Gọi M, N, P lần lượt là hình chiếu của I trên BC, AC, AB.
Khi đó IM = IN = IP.
+) Chứng minh I cách đều ba đỉnh của tam giác ABC.
Xét ∆AIP và ∆AIN có:
\(\widehat {API} = \widehat {AQI} = 90^\circ \)
AI là cạnh chung,
IP = IN (cmt)
Do đó ∆AIP = ∆AIN (cạnh huyền – cạnh góc vuông)
Suy ra AP = AN (hai cạnh tương ứng) và \(\widehat {PAI} = \widehat {NAI}\) (hai góc tương ứng)
Do đó AI là tia phân giác của góc BAC.
Mà \(\widehat {BAC} = 60^\circ \) (do tam giác ABC đều).
Nên \(\widehat {PAI} = \widehat {NAI} = 30^\circ \)
Xét ∆API vuông tại P có:
\(\widehat {PAI} + \widehat {PIA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {PIA} = 90^\circ - \widehat {PAI} = 90^\circ - 30^\circ = 60^\circ \)
Chứng minh tương tự ta có: \(\widehat {PIB} = 60^\circ \)
Xét ∆PIA và ∆PIB có:
\(\widehat {API} = \widehat {BPI} = 90^\circ \)
PI là cạnh chung
\(\widehat {PIA} = \widehat {PIB}\) (cùng bằng 60°)
Do đó ∆PIA = ∆PIB (cạnh góc vuông – góc nhọn kề).
Suy ra IA = IB (hai cạnh tương ứng)
Chứng minh tương tự ta cũng có IB = IC.
Do đó IA = IB = IC nên I cách đều ba đỉnh của tam giác ABC.
Câu 38:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm O . Gọi M là trung điểm của BC; N, P lần lượt là chân đường cao kẻ từ B và C. Đường tròn đi qua 3 điểm M,N,P có phương trình: (T) \({\left( {x - 1} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = \frac{{25}}{4}\). Tìm phương trình đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đường tròn ngoại tiếp tam giác ABC là ảnh của đường tròn (T) qua phép vị tự tâm O tỉ số k = 2
Do đó, phương trình đường tròn ngoại tiếp tam giác:
(x – 2)2 + (y + 1)2 = 25
Vậy phương trình đường tròn ngoại tiếp cần tìm là (x – 2)2 + (y + 1)2 = 25.
Câu 39:
88 – 8 + 8 + 8 +…+8 (11 số 8).
Tính bằng cách thuận tiện nhất.
 Xem đáp án
Xem đáp án
88 – 8 + 8 + 8 +…+8
= 88 – 8 ´ 11
= 88 – 88 = 0.
Câu 40:
Thực hiện phép tính: \(A = \frac{{{3^{10}}.11 + {3^{10}}.5}}{{{3^9}{{.2}^4}}}\).
 Xem đáp án
Xem đáp án
\(A = \frac{{{3^{10}}.11 + {3^{10}}.5}}{{{3^9}{{.2}^4}}} = \frac{{{3^{10}}.\left( {11 + 5} \right)}}{{{3^9}.16}} = \frac{{3.16}}{{16}} = 3\).
Vậy A = 3.
Câu 41:
Cho hình bình hành ABCD, có AC là đường chéo lớn. Kẻ CE vuông góc với AB tại E, BI vuông góc với AC tại I.
Chứng minh rằng:
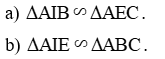
 Xem đáp án
Xem đáp án
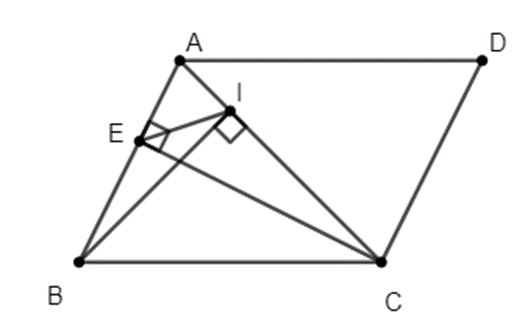
a) Xét ∆AIB và ∆AEC có:
\(\widehat A\) chung
\(\widehat {AEC} = \widehat {AIB} = 90^\circ \)
Do đó (g.g)
Suy ra \(\frac{{AI}}{{AE}} = \frac{{AB}}{{AC}}\) hay \(\frac{{AI}}{{AB}} = \frac{{AE}}{{AC}}\).
b) Xét ∆AIE và ∆ABC có:
\(\widehat A\) chung
\(\frac{{AI}}{{AB}} = \frac{{AE}}{{AC}}\)
Do đó (c.g.c)
Câu 42:
Tính số trung bình cộng của các số sau: 3; 5; 9; 10; 13.
 Xem đáp án
Xem đáp án
Trung bình cộng của các số trên là:
\(\frac{{3 + 5 + 9 + 10 + 13}}{5} = \frac{{40}}{5} = 8\).
Vậy trung bình cộng của các số 3; 5; 9; 10; 13 là 8.
Câu 43:
Một nhóm học sinh có 6 bạn nam và 5 bạn nữ có bao nhiêu cách chọn ra 5 bạn trong đó có cả nam và nữ?
 Xem đáp án
Xem đáp án
Chọn 5 học sinh tùy ý trong 11 học sinh có số cách là: \(C_{11}^5\)
\( \Rightarrow n\left( \Omega \right) = 462\)
Gọi A là biến cố chọn ra 5 học sinh trong đó có cả nam và nữ.
Khi đó \(\overline A \) là biến cố chọn ra 5 học sinh trong đó tất cả là nữ hoặc tất cả là nam.
Suy ra n(\(\overline A \)) = \(C_6^5 + C_5^5 = 6 + 1 = 7\) (Cách)
\( \Rightarrow n(A) = n\left( \Omega \right) - n\left( {\overline A } \right) = 462 - 7 = 455\) (cách)
Vậy có 455 cách chọn ra 5 học sinh trong đó có cả nữ và nam.
Câu 44:
Tính:
a) (x3 + 3x2 – 5x – 1)(4x – 3);
b) \(\left( { - 2{x^2} + 4x + 6} \right)\left( { - \frac{1}{2}x + 1} \right)\).
 Xem đáp án
Xem đáp án
a) (x3 + 3x2 – 5x – 1)(4x – 3);
= 4x4 – 3x3 + 12x3 – 9x2 – 20x2 + 15x – 4x + 3
= 4x4 + (−3x3 + 12x3) + (−9x2 – 20x2) + (15x – 4x) + 3
= 4x4 + 9x3 – 29x2 + 11x + 3.
b) \(\left( { - 2{x^2} + 4x + 6} \right)\left( { - \frac{1}{2}x + 1} \right)\).
= x3 – 2x2 – 2x2 + 4x – 3x + 6
= x3 – 4x2 + x + 6.Câu 45:
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D). So sánh \(\widehat {CAD}\) và \(\widehat {CBD}\).
 Xem đáp án
Xem đáp án
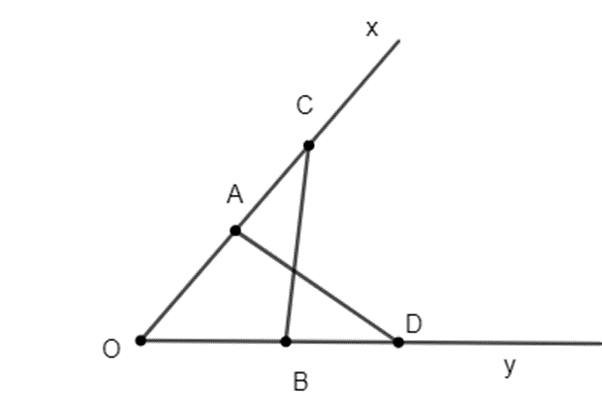
Xét ∆OAD và ∆OBC có:
OA = OB
\(\widehat O\) chung
OC = OD
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra \(\widehat {OBC} = \widehat {OAD}\) (hai góc tương ứng)
Lại có: \(\widehat {OBC} + \widehat {CBD} = 180^\circ \Rightarrow \widehat {CBD} = 180^\circ - \widehat {OBC}\);
\(\widehat {OAD} + \widehat {DAC} = 180^\circ \Rightarrow \widehat {CAD} = 180^\circ - \widehat {OAD}\)
Mà \(\widehat {OBC} = \widehat {OAD}\) (cmt)
Vậy \(\widehat {CBD} = \widehat {CAD}\).
Câu 46:
Cho tam giác ABC vuông tại A, đường cao AH, I là trung điểm của AB, lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D.
a) Tứ giác AKHD là hình gì?
b) Chứng minhAHBD là hình chữ nhật.
 Xem đáp án
Xem đáp án

a) Ta có: H; I lần lượt là trung điểm của BK và AB nên suy ra
HI là đường trung bình của ∆ABK
Suy ra HI // AK hay DH // AK (1)
Mặt khác theo giả thiết ta có: AD // HK (2)
Từ (1) và (2) suy ra tứ giác AKHD là hình bình hành.
b) Vì AKHD là hình bình hành nên:
AD = HK = BH
Mà AD//BH nên AHBD là hình bình hành.
Lại có: \(\widehat {AHB} = 90^\circ \)
Suy ra AHBD là hình chữ nhật.
Câu 47:
 Xem đáp án
Xem đáp án
Ta có: A = x4 + 2x3 – x2 – 2x
= (x4 – x3) + (3x3 – 3x2) + (2x2 – 2x)
= x3(x – 1) + 3x2(x – 1) + 2x(x – 1)
= (x – 1)(x3 + 3x2 + 2x)
= (x – 1)x(x2 + x + 2x + 2)
= (x – 1)x[x(x + 1) + 2(x + 1)]
= (x – 1)x(x + 1)(x + 2).
Ta thấy \(\forall \)x ∈ ℤ thì A là tích của 4 số liên tiếp nên chắc chắc A ⋮ 2; A ⋮ 3; A ⋮ 4.
Từ đó suy ra A ⋮ (2.3.4) hay A ⋮ 24 (đpcm).
Câu 48:
Tìm nghiệm nguyên dương của phương trình: \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{6xy}} = \frac{1}{6}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{6xy}} = \frac{1}{6}\)
⇔ 6x + 6y + 1 = xy
⇔ 6x + 6y + 1 – xy = 0
⇔ xy – 6x – 6y + 36 – 37 = 0
⇔ (xy – 6x) – (6y – 36) = 37
⇔ x(y – 6) – 6(y – 6) = 37
⇔ (x – 6)(y – 6) = 37
Vì x, y là số nguyên dương nên (x – 6)(y – 6) ∈ Ư(37) .
Ư(37) = {1; 37}
\( \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 6 = 1\\y - 6 = 37\end{array} \right.\\\left\{ \begin{array}{l}x - 6 = 37\\y - 6 = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 7\\y = 43\end{array} \right.\\\left\{ \begin{array}{l}x = 43\\y = 7\end{array} \right.\end{array} \right.\)
Vây (x; y) ∈ {(7; 43), (43; 7)}.
Câu 49:
Lớp 5A có một số học sinh. Biết số học sinh nữ bằng \(\frac{2}{3}\) số học sinh cả lớp. Hỏi số học sinh nam chiếm bao nhiêu phần trăm số học sinh cả lớp?
 Xem đáp án
Xem đáp án
Số học sinh nam chiếm số phần trăm số học sinh cả lớp là:
\(\left( {1 - \frac{2}{3}} \right) \times 100\% = \frac{1}{3} \times 100\% = 33,33\% \)
Đáp số: 33,33%
Câu 50:
Phân tích đa thức thành nhân tử: 36 + 2xy – x2 – y2.
 Xem đáp án
Xem đáp án
36 + 2xy – x2 – y2
= 36 – (x2 – 2xy + y2)
= 62 – (x – y)2
= (6 + x – y)(6 – x + y)