Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ.
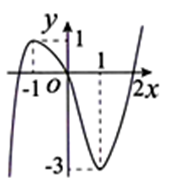Số nghiệm thực của phương trình f(2 + f(ex)) = 1 là:
Giải bởi Vietjack
Lời giải
Đáp án đúng là: B
Số nghiệm của phương trình f(2 + f(ex)) = 1 là số giao điểm của đồ thị hàm số y = f(2 + f(ex)) và đường thẳng y = 1
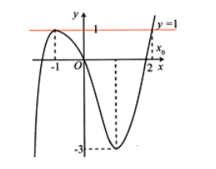
Dựa vào đồ thị hàm số ta có:
\(f\left( {2 + f\left( {{e^x}} \right)} \right) = 1\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2 + f\left( {{e^x}} \right) = - 1}\\{2 + f\left( {{e^x}} \right) = {x_0} \in (2;3)}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( {{e^x}} \right) = - 3}\\{f\left( {{e^x}} \right) = {x_0} - 2 \in (0;1)}\end{array}} \right.\)
TH1: f(ex) = –3
\( \Leftrightarrow \left[ \begin{array}{l}{e^x} = 1\\{e^x} = {x_1} < - 1\end{array} \right. \Leftrightarrow x = 0\)
TH2: f(ex) = x0 – 2 ∈ (0; 1)
Suy ra phương trình có 3 nghiệm khác 0
Do đó: \(\left[ \begin{array}{l}{e^x} = a < 0\\{e^x} = b < 0\\{e^x} = c > 0\end{array} \right. \Leftrightarrow x = \ln c \ne 0\)
Vậy phương trình có 2 nghiệm phân biệt.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.
a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Giả sử BC = 2a. Tính BM . CN.
d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2cm và OA = 4cm.
Cho đường tròn tâm O đường kính AB. Lấy điểm C thuộc đường tròn, với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn tâm O tại tiếp điểm C cắt tia OI tại điểm D.
a) Chứng minh OI // BC.
b) Chứng minh DA là tiếp tuyến của đường tròn tâm O.
c) Vẽ CH ⊥ AB (H ∈ AB) và BK ⊥ CD (K ∈ CD). Chứng minh CK2 = HA . HB.
Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất:
