Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.
Giải bởi Vietjack
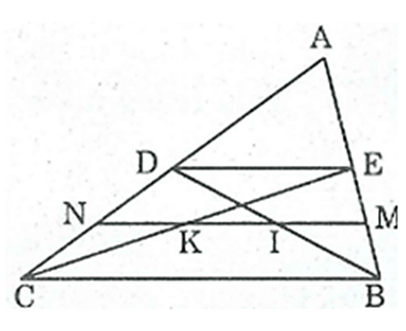
Trong ΔABC ta có:
E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ΔABC
⇒ ED // BC và \[ED = \frac{1}{2}BC\] (tính chất đường trung bình của tam giác)
Tứ giác BCDE có: ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE
⇒ MN // DE
Áp dụng tính chất đường trung bình hình thang ta có:
\[MN = \frac{1}{2}\left( {DE + BC} \right) = \frac{1}{2}\left( {\frac{1}{2}BC + BC} \right) = \frac{3}{4}BC\]
Trong ΔBED, ta có:
M là trung điểm BE
MI // DE
Þ MI là đường trung bình của ΔBED
\[ \Rightarrow MI = \frac{1}{2}DE = \frac{1}{4}BC\] (tính chất đường trung bình của tam giác)
Trong ΔCED ta có:
N là trung điểm CD
NK // DE
Þ NK là đường trung bình của ΔCED
\[ \Rightarrow NK = \frac{1}{2}DE = \frac{1}{4}BC\] (tính chất đường trung bình của tam giác)
\[ \Rightarrow IK = MN - (MI + NK) = \frac{3}{4}BC - \frac{1}{4}BC - \frac{1}{4}BC = \frac{1}{4}BC\]
\[ \Rightarrow MI = IK = NK = \frac{1}{4}BC\]
Vậy MI = IK = KN.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC cân tại A có AM là đường phân giác (M thuộc BC) Qua điểm M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh tam giác MNC là tam giác cân.
Cho tam giác ABC cân tại A có AM là đường phân giác (M thuộc BC) Qua điểm M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh \[\widehat {NAM} = \widehat {NMA}\].
Cho tam giác ABC có đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M, N lần lượt là trung điểm của BC, CE. Gọi I, K lần lượt là giao điểm của AM, AN với BE. Chứng minh BI = IK = KE.
Trong kì thi THPT Quốc Gia, mỗi phòng thi gồm 24 thí sinh được sắp xếp vào 24 bàn khác nhau. Bạn Nam là một thí sinh dự thi, bạn đăng kí 4 môn thi và cả 4 lần đều thi tại 1 phòng duy nhất. Giả sử giám thị xếp thí sinh vào vị trí một cách ngẫu nhiên, tính xác suất để trong 4 lần thi thì bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí.
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm. Tính BC, AH.
Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm b sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh: AB vuông góc với OI.
Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là trung trực của EF.
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?
Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh AM là trung trực của BC.
Cho ∆ABC cân tại A có M là trung điểm BC, đường cao CN cắt AM tại H. Chứng minh BH ^ AC.
Rút gọn biểu thức: \[A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}\].
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm. Tính BH, CH.
Cho hình thang vuông ABCD (\[\widehat A = \widehat D = 90^\circ \]). E là trung điểm của AD và \[\widehat {BEC} = 90^\circ \]. Cho biết AD = 2a. Chứng minh rằng: ΔEAB đồng dạng ΔCEB.
