Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 80)
-
1329 lượt thi
-
83 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho \[A = \left( { - \infty ;\,\,2} \right];\,\,B = \left[ {3;\,\, + \infty } \right);\,\,C = \left( {0;\,\,4} \right)\]. Tìm A ∩ B, (A ∪ B) ∩ C.
 Xem đáp án
Xem đáp án
Cho \[A = \left( { - \infty ;\,\,2} \right];\,\,B = \left[ {3;\,\, + \infty } \right);\,\,C = \left( {0;\,\,4} \right)\]. Tìm A ∩ B, (A ∪ B) ∩ C.
Câu 2:
Cho A = [−4; 7], B = (−∞; −2) ∪ (3; +∞). Tìm A ∩ B.
 Xem đáp án
Xem đáp án
Ta có: A = [−4; 7], B = (−∞; −2) ∪ (3; +∞)
Do đó A ∩ B = [−4; −2) ∪ (3; 7].
Vậy A ∩ B = [−4; −2) ∪ (3; 7].
Câu 3:
Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax, By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn. Qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C, D. Chứng minh rằng CD = AC + BD, \[\widehat {COD} = 90^\circ \].
 Xem đáp án
Xem đáp án
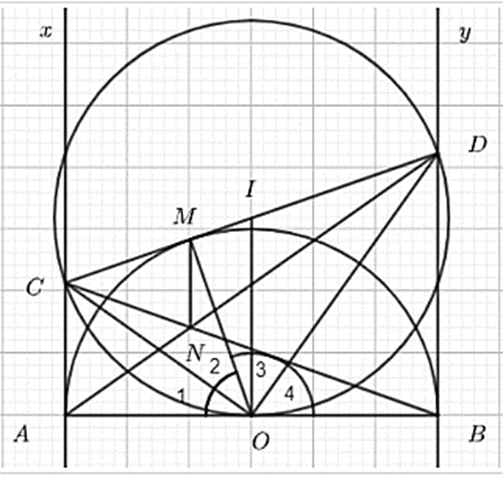
Do CA và CM là hai tiếp tuyến cắt nhau nên CA = CM
Do DM và DB là hai tiếp tuyến cắt nhau nên DM = DB
Suy ra CD = CM + MD = CA + DB (đpcm)
Ta có: \[{\widehat O_1} = {\widehat O_2}\] (tính chất 2 tiếp tuyến cắt nhau)
và \[{\widehat O_3} = {\widehat O_4}\] (tính chất 2 tiếp tuyến cắt nhau)
\[ \Rightarrow \widehat {COD} = {\widehat O_2} + {\widehat O_3} = \frac{1}{2}\left( {{{\widehat O}_1} + {{\widehat O}_2} + {{\widehat O}_3} + {{\widehat O}_4}} \right) = 90^\circ \]
Vậy CD = AC + BD, \[\widehat {COD} = 90^\circ \].
Câu 4:
Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn. Qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C, D. Chứng minh rằng AC. BD = R2.
 Xem đáp án
Xem đáp án
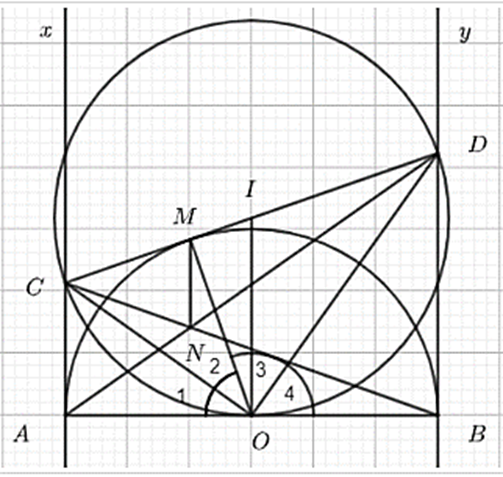
Ta có: \[{\widehat O_1} = {\widehat O_2}\] (tính chất 2 tiếp tuyến cắt nhau)
và \[{\widehat O_3} = {\widehat O_4}\] (tính chất 2 tiếp tuyến cắt nhau)
\[ \Rightarrow \widehat {COD} = {\widehat O_2} + {\widehat O_3} = \frac{1}{2}\left( {{{\widehat O}_1} + {{\widehat O}_2} + {{\widehat O}_3} + {{\widehat O}_4}} \right) = 90^\circ \]
Þ ΔCOD vuông tại O, có đường cao OM
Do CA và CM là hai tiếp tuyến cắt nhau nên CA = CM
Do DM và DB là hai tiếp tuyến cắt nhau nên DM = DB
Áp dụng hệ thức lượng ta có:
OM2 = CM. MD
⇒ R2 = CA. DB (đpcm)
Vậy AC. BD = R2.
Câu 5:
Hình thang ABCD (AB // CD) có \[\widehat D = 70^\circ \], \[\widehat A = 2\widehat C\]. Tính số đo các góc còn lại.
 Xem đáp án
Xem đáp án
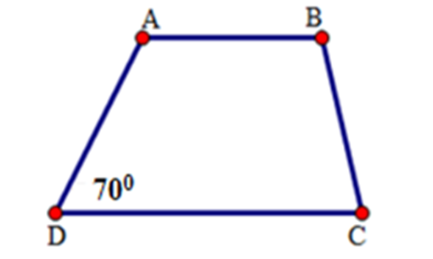
Ta có: \[\widehat A + \widehat D = 180^\circ \]
\[ \Rightarrow \widehat A = 180^\circ - \widehat D = 180^\circ - 70^\circ = 110^\circ \]
\[ \Rightarrow \widehat C = \frac{1}{2}\widehat A = \frac{1}{2} \cdot 110^\circ = 55^\circ \]
\[ \Rightarrow \widehat B = 180^\circ - \widehat C = 180^\circ - 55^\circ = 125^\circ \]
Vậy \[\widehat A = 110^\circ ;\,\,\,\,\widehat B = 125^\circ ;\,\,\,\widehat C = 55^\circ \].
Câu 6:
Cho tam giác ABC có AB = 4 cm, AC = 6 cm, \[\widehat A = 120^\circ \]. Tính độ dài cạnh BC.
 Xem đáp án
Xem đáp án
Áp dụng định lí côsin trong tam giác ta có:
BC2 = AB2 + AC2 − 2AB.AC.cos\[\widehat A\]= 42 + 62 − 2.4.6.cos120°
= 16 + 36 + 24 = 76
\[ \Rightarrow BC = \sqrt {76} \approx 8,72\]
Vậy BC = 8,72 cm.
Câu 7:
Cho tam giác ABC có cạnh AB = 14 cm, \[\widehat C = 120^\circ \], tổng hai cạnh còn lại là 16 cm. Tính độ dài hai cạnh còn lại.
 Xem đáp án
Xem đáp án
Theo định lí cosin, ta có:
AB2 = BC2 + AC2 – 2.BC.AC.cos\[\widehat C\]
⇔ 196 = BC2 + AC2 – 2.BC.AC.cos120°
⇔ 196 = BC2 + AC2 + BC.AC (1)
Ta lại có: BC + AC = 16 ⇒ AC = 16 – BC thay vào (1), ta được:
196 = BC2 + (16 – BC)2 + BC(16 – BC)
⇔ BC2 – 16BC + 60 = 0
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{BC = 10}\\{BC = 6\,\,}\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{AC = 6\,\,\,}\\{AC = 10\,}\end{array}} \right.\]
Vậy AC = 6 cm và BC = 10 cm hoặc AC = 10 cm và BC = 6 cm.
Câu 8:
Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh AM là trung trực của BC.
 Xem đáp án
Xem đáp án
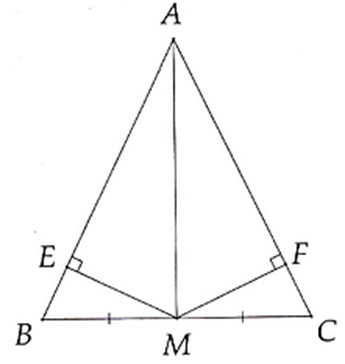
ΔABC cân tại A nên AB = AC
M là trung điểm của BC nên MB = MC
Þ AM là đường trung trực của BC (tính chất đường trung trực của đoạn thẳng)
Vậy AM là đường trung trực của BC.
Câu 9:
Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là trung trực của EF.
 Xem đáp án
Xem đáp án
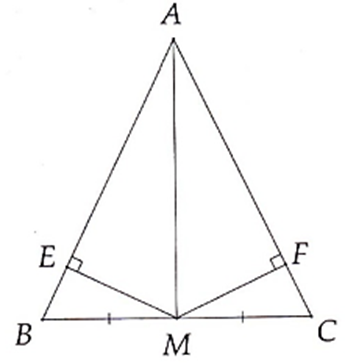
ΔABC cân tại A nên \[\widehat B = \widehat C\]
Xét ΔBEM và ΔCFM có:
MB = MB (vì M là trung điểm BC)
\[\widehat B = \widehat C\]
\[\widehat E = \widehat F = 90^\circ \]
Do đó ΔBEM = ΔCFM (cạnh huyền – góc nhọn)
Suy ra ME = MF (hai cạnh tương ứng).
Mà AB = AC (vì ΔABC cân)
Þ AB – BE = AC – CF
Hay AE = AF
Mà ME = MF
Þ AM là đường trung trực của EF (tính chất đường trung trực của đoạn thẳng)
Vậy ME = MF và AM là đường trung trực của EF.
Câu 10:
Cho ∆ABC cân tại A, đường trung tuyến CM. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Chứng minh CD = 2CM.
 Xem đáp án
Xem đáp án
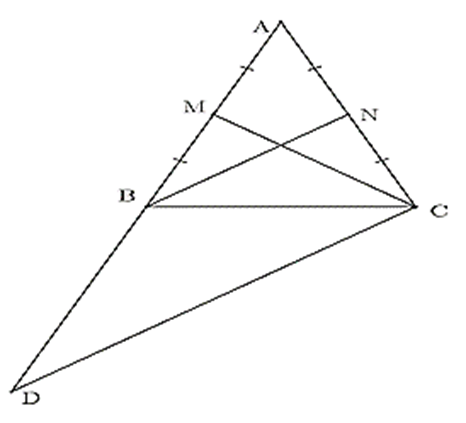
Gọi N là trung điểm cạnh AC
\[ \Rightarrow AN = \frac{1}{2}AC\]
\[ \Rightarrow AM = AN = \frac{1}{2}AB\](vì AB = AC)
Xét ΔABN và ΔACM có:
AB = AC
\[\widehat A\] chung
AM = AN
Do đó ΔABN = ΔACM (c.g.c)
Suy ra BN = CM (hai cạnh tương ứng)
Vì ΔABC là tam giác cân tại A nên dễ dàng chứng minh được BN = CM
Xét ΔACD có B, N lần lượt là trung điểm cạnh AD và AC.
Suy ra BN là đường trung bình của tam giác của ΔACD.
\[ \Rightarrow BN = \frac{1}{2}DC\]
⇒ DC = 2BN (2)
Từ (1) và (2) suy ra CD = 2CM
Vậy CD = 2CM.
Câu 11:
Cho tam giác ABC có \[\widehat B = 60^\circ ;\,\,\widehat C = 45^\circ \], AB = 10,6 cm. Tính CA, CB.
 Xem đáp án
Xem đáp án
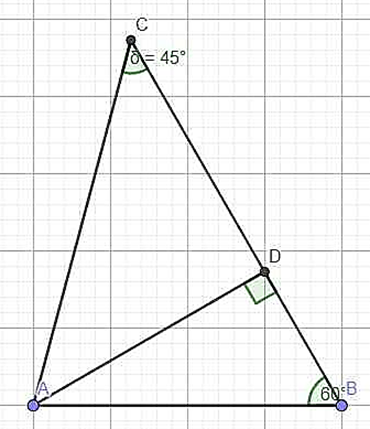
Kẻ đường cao AD ứng với BC
Trong tam giác vuông ABD có:
\[\sin \widehat B = \frac{{AD}}{{AB}} \Rightarrow AD = AB.\sin \widehat B = 10,6.\sin 60^\circ \approx 9,2\]
\[\cos \widehat B = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\cos \widehat B = 10,6.\cos 60^\circ \approx 5,3\]
Trong tam giác vuông ACD có:
\[\tan \widehat C = \frac{{AD}}{{CD}} \Rightarrow CD = AD.\tan \widehat C = 9,2.\tan 45^\circ = 9,2\]
\[\sin \widehat C = \frac{{AD}}{{AC}} \Rightarrow AC = \frac{{AD}}{{\sin \widehat C}} = \frac{{9,2}}{{\sin 45^\circ }} \approx 13\]
BC = BD + CD = 5,3 + 9,2 = 14,5 (cm)
Vậy AC = 13 cm; BC = 14,5 cm.
Câu 12:
Cho tam giác ABC có đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M, N lần lượt là trung điểm của BC, CE. Gọi I, K lần lượt là giao điểm của AM, AN với BE. Chứng minh BI = IK = KE.
 Xem đáp án
Xem đáp án
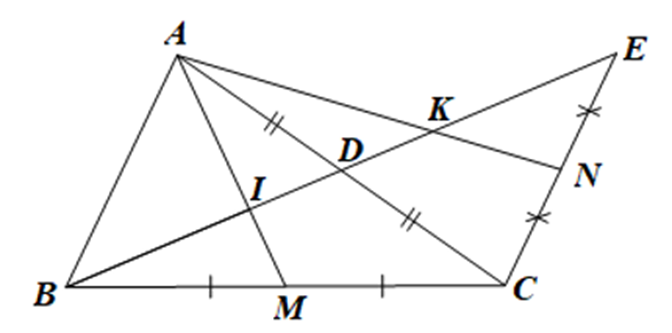
Xét tam giác ABC có BD và AM là các đường trung tuyến, BD cắt AM tại I.
Suy ra I là trọng tâm của tam giác ABC
Nên \[BI = \frac{2}{3}BD\,\,(1)\]
Xét tam giác AEC có ED và AN là các đường trung tuyến, ED cắt AN tại K.
Suy ra K là trọng tâm của tam giác AEC.
Nên \[EK = \frac{2}{3}ED\,\,(2)\]
Mặt khác BD = DE, DB + DE = BE
Nên \[BD = DE = \frac{1}{2}BE\,\,\](3)
Từ (1), (2) và (3) ta có:
\[BI = EK = \frac{2}{3}BD = \frac{2}{3} \cdot \frac{1}{2}BE\,\, = \frac{1}{3}BE\]
Ta lại có: BI + IK + KE = BE
\[\, \Rightarrow \frac{1}{3}BE + IK + \frac{1}{3}BE = BE\]
\[ \Rightarrow IK = \frac{1}{3}BE\]
Do đó BI = IK = EK (cùng bằng \[\frac{1}{3}BE\])
Vậy BI = IK = EK.
Câu 13:
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.
 Xem đáp án
Xem đáp án
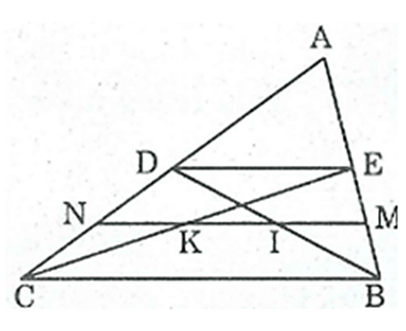
Trong ΔABC ta có:
E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ΔABC
⇒ ED // BC và \[ED = \frac{1}{2}BC\] (tính chất đường trung bình của tam giác)
Tứ giác BCDE có: ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE
⇒ MN // DE
Áp dụng tính chất đường trung bình hình thang ta có:
\[MN = \frac{1}{2}\left( {DE + BC} \right) = \frac{1}{2}\left( {\frac{1}{2}BC + BC} \right) = \frac{3}{4}BC\]
Trong ΔBED, ta có:
M là trung điểm BE
MI // DE
Þ MI là đường trung bình của ΔBED
\[ \Rightarrow MI = \frac{1}{2}DE = \frac{1}{4}BC\] (tính chất đường trung bình của tam giác)
Trong ΔCED ta có:
N là trung điểm CD
NK // DE
Þ NK là đường trung bình của ΔCED
\[ \Rightarrow NK = \frac{1}{2}DE = \frac{1}{4}BC\] (tính chất đường trung bình của tam giác)
\[ \Rightarrow IK = MN - (MI + NK) = \frac{3}{4}BC - \frac{1}{4}BC - \frac{1}{4}BC = \frac{1}{4}BC\]
\[ \Rightarrow MI = IK = NK = \frac{1}{4}BC\]
Vậy MI = IK = KN.
Câu 14:
 Xem đáp án
Xem đáp án
a5 – a = a(a4 – 1) = a(a2 – 1)(a2 + 1) = a(a – 1)(a + 1)(a2 – 4 + 5)
= a(a – 1)(a + 1)(a2 – 4) + 5a(a – 1)(a + 1)
= a(a – 1)(a + 1)(a – 2)(a + 2) + 5a(a – 1)(a + 1)
Do a(a – 1)(a + 1)(a – 2)(a + 2) là tích 5 số nguyên liên tiếp nên tồn tại 1 số chia hết cho 2; 1 số chia hết cho 3 và 1 số chia hết cho 5
Þ a(a – 1)(a + 1)(a – 2)(a + 2) chia hết cho 30
Mặt khác, a(a – 1)(a + 1) là tích 3 số nguyên liên tiếp nên a(a – 1)(a + 1) chia hết cho 6
Þ 5a(a – 1)(a + 1) chia hết cho 30
Þ a(a – 1)(a + 1)(a – 2)(a + 2) + 5a(a – 1)(a + 1) chia hết cho 30
Vậy a5 – a chia hết cho 30.
Câu 15:
Đoạn đường AB dài 1 km gồm hai đoạn AM và MB. Đoạn AM = \[\frac{2}{3}\] đoạn MB. Hãy tính độ dài của đoạn đường MB.
 Xem đáp án
Xem đáp án
Đổi: 1 km = 1000 m
Ta có sơ đồ:

Độ dài đoạn đường MB là:
1000 : (2 + 3) ´ 3 = 600 (m)
Đáp số: 600 m
Câu 16:
Cho tam giác ABC cân tại A có AM là đường phân giác (M thuộc BC) Qua điểm M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh \[\widehat {NAM} = \widehat {NMA}\].
 Xem đáp án
Xem đáp án
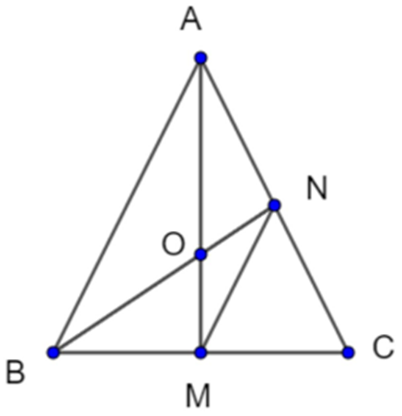
Ta có: MN // AB
\[ \Rightarrow \widehat {BAM} = \widehat {AMN}\] (vì so le trong)
mà \[\widehat {BAM} = \widehat {CAM}\] (vì AM là phân giác \[\widehat A\])
\[ \Rightarrow \widehat {AMN} = \widehat {CAM}\] hay \[\widehat {NAM} = \widehat {NMA}\]
Vậy \[\widehat {NAM} = \widehat {NMA}\].
Câu 17:
Cho tam giác ABC cân tại A có AM là đường phân giác (M thuộc BC) Qua điểm M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh tam giác MNC là tam giác cân.
 Xem đáp án
Xem đáp án
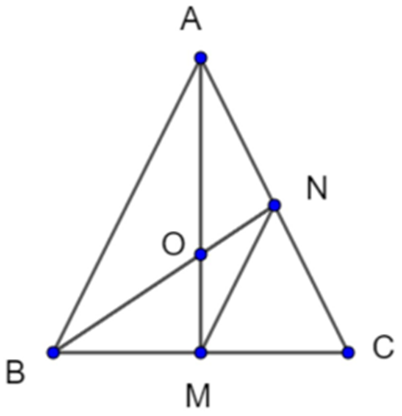
Ta có: MN // AB
\[ \Rightarrow \widehat {ABC} = \widehat {NMC}\] (vì đồng vị)
ΔABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\]
\[ \Rightarrow \widehat {ACB} = \widehat {NMC}\]
Þ ΔMNC cân tại N
Vậy ΔMNC cân tại N.
Câu 18:
Tìm giá trị nhỏ nhất của biểu thức \[A = \frac{{2{m^2} - 4m + 5}}{{{m^2} - 2m + 2}}\].
 Xem đáp án
Xem đáp án
Ta có: \[A = \frac{{2{m^2} - 4m + 5}}{{{m^2} - 2m + 2}}\]
\[A = \frac{{2{m^2} - 4m + 2 + 3}}{{{m^2} - 2m + 1 + 1}}\]
\[A = \frac{{2\left( {{m^2} - 2m + 1} \right) + 3}}{{{m^2} - 2m + 1 + 1}}\]
\[A = \frac{{2{{\left( {m - 1} \right)}^2} + 3}}{{{{\left( {m - 1} \right)}^2} + 1}} \ge \frac{3}{1} = 3\] (do (m – 1)2 ≥ 0)
Dấu “=” xảy ra Û m – 1 = 0 Û m = 1
Vậy giá trị nhỏ nhất của A là 3 khi m = 1.
Câu 19:
 Xem đáp án
Xem đáp án
Ta có: P = x2 + 2xy + 3y2 + 5y + 10
= (x2 + 2xy + y2) + (2y2 + 5y + 10)
\[ = {(x + y)^2} + 2{\left( {{y^2} + \frac{5}{2}y + 5} \right)^2} = {(x + y)^2} + 2\left( {{y^2} + \frac{5}{2}y + \frac{{25}}{{16}} + \frac{{55}}{{16}}} \right)\]
\[ = {(x + y)^2} + 2{\left( {y + \frac{5}{4}} \right)^2} + \frac{{55}}{8} \ge \frac{{55}}{8}\]
Dấu "=" xảy ra \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + y = 0}\\{y + \frac{5}{4} = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{5}{4}}\\{y = \frac{{ - 5}}{4}}\end{array}} \right.\]
Vậy giá trị nhỏ nhất của \[P = \frac{{55}}{8}\] khi \[x = \frac{5}{4};\,\,y = \frac{{ - 5}}{4}\].
Câu 20:
Tìm trung bình cộng của các số 10; 30; 50; 70.
 Xem đáp án
Xem đáp án
Trung bình cộng của 4 số đó là:
(10 + 30 + 50 + 70) : 4 = 40
Đáp số: 40
Câu 21:
Tìm trung bình cộng của dãy số sau: 14; 20; 26; 32; … ; 86.
 Xem đáp án
Xem đáp án
Số số hạng của dãy số trên là:
(86 – 14) : 6 + 1 = 13 (số)
Tổng của dãy số trên là:
(14 + 86) ´ 13 : 2 = 650
Trung bình cộng của dãy số trên là:
650 : 13 = 50
Đáp số: 50
Câu 22:
Giải phương trình: sin(2x + 1) = cos(3x + 2).
 Xem đáp án
Xem đáp án
sin(2x + 1) = cos(3x + 2)
\[ \Leftrightarrow \sin (2x + 1) = \sin \left( {\frac{\pi }{2} - 3x - 2} \right)\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 1 = \frac{\pi }{2} - 3x - 2 + k2\pi }\\{2x + 1 = \pi - \frac{\pi }{2} + 3x + 2 + k2\pi }\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{10}} - \frac{3}{5} + \frac{{k2\pi }}{5}}\\{x = - \frac{\pi }{2} - 1 - k2\pi }\end{array}} \right.\,\,(k \in \mathbb{Z})\]
Vậy giá trị x cần tìm là \[x = \frac{\pi }{{10}} - \frac{3}{5} + \frac{{k2\pi }}{5}\] hoặc \[x = - \frac{\pi }{2} - 1 - k2\pi \].
Câu 23:
Giải phương trình: \[\sin 3x - \sqrt 3 \cos 3x = 2\sin 2x\].
 Xem đáp án
Xem đáp án
Ta có: \[\sin 3x - \sqrt 3 \cos 3x = 2\sin 2x\]
\[ \Leftrightarrow 2\sin \left( {3x - \frac{\pi }{3}} \right) = 2\sin 2x\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - \frac{\pi }{3} = 2x + k2\pi }\\{3x - \frac{\pi }{3} = \pi - 2x + k2\pi }\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{{2\pi }}{{15}} + \frac{{k2\pi }}{5}}\end{array}} \right.\,\,(k \in \mathbb{Z})\]
Vậy các giá trị x thoả mãn là \[x = \frac{\pi }{3} + k2\pi \] hoặc \[x = \,\frac{{2\pi }}{{15}} + \frac{{k2\pi }}{5}\].
Câu 24:
Có bao nhiêu cách sắp xếp 20 thí sinh vào một phòng thi có 20 bàn mỗi bàn một thí sinh.
 Xem đáp án
Xem đáp án
Mỗi cách xếp 20 thí sinh vào 20 vị trí của một phòng thi là một hoán vị của 20 phần tử,
Số cách xếp là:
P20 = 20! (cách)
Vậy có 20! cách sắp xếp thoả mãn đề bài.
Câu 25:
Trong kì thi THPT Quốc Gia, mỗi phòng thi gồm 24 thí sinh được sắp xếp vào 24 bàn khác nhau. Bạn Nam là một thí sinh dự thi, bạn đăng kí 4 môn thi và cả 4 lần đều thi tại 1 phòng duy nhất. Giả sử giám thị xếp thí sinh vào vị trí một cách ngẫu nhiên, tính xác suất để trong 4 lần thi thì bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí.
 Xem đáp án
Xem đáp án
Số phần tử của không gian mẫu là:
n(W) = (24!)4
Gọi A : “Bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí”
Chọn 2 lượt thi mà Nam ngồi trùng vị trí có: \[C_4^2\] cách
Trong 2 lượt đó, lượt đầu: Nam có 24 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại; lượt sau: Nam có 1 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại.
\[A_{23}^2.{(23!)^2}\]
\[n(A) = (24.23!)(1.23!).\left( {A_{23}^2.{{(23!)}^2}} \right)\]
\[ = {(23!)^4}.24.22\]
\[ \Rightarrow P(A) = \frac{{C_4^2.{{(23!)}^4}.24.23.22}}{{{{(24!)}^4}}}\]
\[ = \frac{{6.23.22}}{{24.24.24}} = \frac{{253}}{{1152}}\]
Vậy xác suất để trong 4 lần thi bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí là \[\frac{{253}}{{1152}}\].
Câu 26:
Cho sin x + cos x = m. Tính theo m giá trị của M = sin x.cos x.
 Xem đáp án
Xem đáp án
Ta có: sin x + cos x = m
⇔ (sin x + cos x)2 = m2
⇔ sin2 x + 2sin x.cos x + cos2x = m2
⇔ (sin2 x + cos2 x) + 2sin x.cos x = m2
⇔ 1 + 2sin x.cos x = m2
\[ \Leftrightarrow \sin x.\cos x = \frac{{{m^2} - 1}}{2}\]
\[ \Rightarrow M = \frac{{{m^2} - 1}}{2}\]
Vậy \[M = \frac{{{m^2} - 1}}{2}\].
Câu 27:
Rút gọn biểu thức: \[A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}\].
 Xem đáp án
Xem đáp án
\[A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}\]
\[ \Leftrightarrow 2A = 2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2011}}}}\]
\[ \Leftrightarrow 2A - A = \left( {2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2011}}}}} \right) - \left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{2012}}}}} \right)\]
\[ \Leftrightarrow 2A - A = 2 - \frac{1}{{{2^{2012}}}}\]
\[ \Leftrightarrow A = \frac{{{2^{2012}} + 1}}{{{2^{2012}}}}\]
Vậy \[A = \frac{{{2^{2012}} + 1}}{{{2^{2012}}}}\].
Câu 28:
Rút gọn biểu thức: A = 1 + 3 + 32 + 33 + … + 399 + 3100.
 Xem đáp án
Xem đáp án
A = 1 + 3 + 32 + 33 + … + 399 + 3100
Ta có: 3A = 3 + 32 + 33 + … + 399 + 3100 + 3101
Khi đó:
3A – A = (3 + 32 + 33 + … + 399 + 3100 + 3101) – (1 + 3 + 32 + 33 + … + 399 + 3100)
= 3101 – 1.
Û 2A = 3101 – 1
\[ \Leftrightarrow A = \frac{{{3^{101}} - 1}}{2}\]
Vậy \[A = \frac{{{3^{101}} - 1}}{2}\].
Câu 29:
Cho ngũ giác đều ABCDE có tâm là điểm O. Chứng minh rằng: \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} = \overrightarrow 0 \].
 Xem đáp án
Xem đáp án
Đặt \[\overrightarrow u = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} \]
Ta có: \[\overrightarrow u = \overrightarrow {OA} + \left( {\overrightarrow {OB} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right)\].
Do OA nằm trên đường phân giác của \[\widehat {BOE}\] và \[\widehat {DOC}\] của hai tam giác cân BOE và DOC nên ta có các \[\overrightarrow {OB} + \overrightarrow {OE} \] và \[\overrightarrow {OC} + \overrightarrow {OD} \] nằm trên đường thẳng OA
Þ \[\overrightarrow u \] nằm trên đường thẳng OA.
Chứng minh tương tự ta có \[\overrightarrow u \]cũng đồng thời nằm trên đường thẳng OB.
Mà OA và OB không cùng phương nên \[\overrightarrow u = \overrightarrow 0 \].
Vậy \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} = \overrightarrow 0 \].
Câu 30:
Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.
 Xem đáp án
Xem đáp án
A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.
A ∩ B: tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.
A \ B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.
B \ A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.
Câu 31:
Cho hai tập hợp:
A = {1; 3}
B = {1; 2}
Tìm A ∪ B ; A ∩ B ; A \ B ; B \ A.
 Xem đáp án
Xem đáp án
Ta có: A = {1; 3} và B = {1; 2}
A ∪ B={1; 2; 3}
A ∩ B = {1}
A \ B = {3}
B \ A = {2}
Câu 32:
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?
 Xem đáp án
Xem đáp án
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
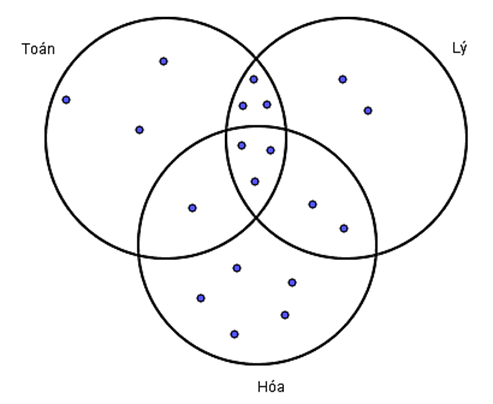
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là:
6 – 3 = 3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là:
4 – 3 = 1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là:
5 – 3 = 2 (em)
Số học sinh chỉ giỏi một môn Toán là:
10 – 3 – 3 – 1 = 3 (em)
Số học sinh chỉ giỏi một môn Lý là:
10 – 3 – 3 – 2 = 2 (em)
Số học sinh chỉ giỏi một môn Hóa là:
11 – 1 – 3 – 2 = 5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3 + 2 + 5 + 1 + 2 + 3 + 3 =19 (em)
Đáp số: 19 em
Câu 33:
Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?
 Xem đáp án
Xem đáp án
Ta có sơ đồ Ven:
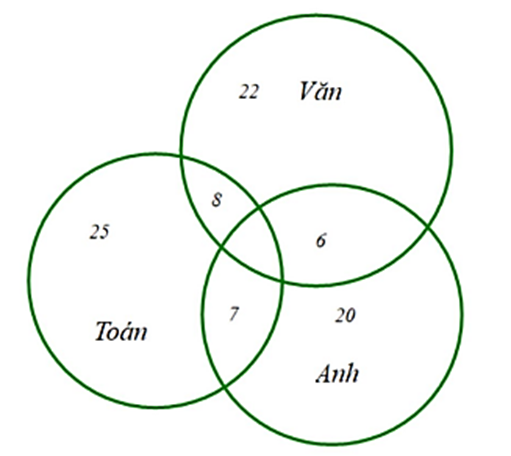
Số học sinh giỏi ít nhất hai môn là:
7 + 6 + 8 = 21 (em)
Vậy số học sinh giỏi cả ba môn Toán, Văn, Anh là:
22 + 25 + 20 – 40 – 21 = 6 (em)
Đáp số: 6 em.
Câu 34:
Giải phương trình: cos2 3x = 1.
 Xem đáp án
Xem đáp án
cos2 3x = 1
Û sin2 3x = 0
Û sin 3x = 0
\[ \Leftrightarrow 3x = k\pi \,\,(k \in \mathbb{Z})\]
\[ \Leftrightarrow x = \frac{{k\pi }}{3}\,\,(k \in \mathbb{Z})\]
Vậy \[x = \frac{{k\pi }}{3}\,\,(k \in \mathbb{Z})\].
Câu 35:
Tìm nghiệm của phương trình nằm trong \[\left[ {0;2\pi } \right)\].
sin 2x + sin x = 0.
 Xem đáp án
Xem đáp án
Ta có: sin 2x + sin x = 0
Û sin 2x = –sin x
Û sin 2x = sin (–x)
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = - x + k2\pi \,\,\,\,\,}\\{2x = \pi + x + k2\pi }\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = k2\pi \,\,\,\,\,}\\{x = \pi + k2\pi }\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k2\pi \,}}{3}\,\,\,\,\,\,\,}\\{x = \pi + k2\pi }\end{array}} \right.\]
Vì \[x \in \left[ {0;2\pi } \right)\] nên tập nghiệm của phương trình là \[S = \left\{ {0;\,\,\frac{{2\pi }}{3};\,\,\pi ;\,\,\frac{{4\pi }}{3}} \right\}\].
Vậy tập nghiệm của phương trình là \[S = \left\{ {0;\,\,\frac{{2\pi }}{3};\,\,\pi ;\,\,\frac{{4\pi }}{3}} \right\}\].
Câu 36:
Tìm x, biết: 42x – 3 = 214.
 Xem đáp án
Xem đáp án
42x – 3 = 214
42x – 3 = (22)7
42x – 3 = 47
Û 2x – 3 = 7
Û 2x = 10
Û x = 5
Vậy x = 5.
Câu 37:
Giải phương trình: \[{\left( {\frac{1}{2}} \right)^{1 - 2x}} = {2^{9 - 3x}}\].
 Xem đáp án
Xem đáp án
\[{\left( {\frac{1}{2}} \right)^{1 - 2x}} = {2^{9 - 3x}}\]
Û (2– 1)1 – 2x = 29 – 3x
Û 22x – 1 = 29 – 3x
Û 2x – 1 = 9 – 3x
Û 5x = 10
Û x = 2
Vậy nghiệm của phương trình đã cho là x = 2.
Câu 38:
Xác định các tập hợp A ∪ B và A ∩ B với: A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
 Xem đáp án
Xem đáp án
Tập A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím}.
Các phần tử vừa thuộc tập hợp A và B là: lục; lam.
Do đó A ∩ B = {lục; lam}.
Vậy A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím} và A ∩ B = {lục; lam}.
Câu 39:
Xác định các tập hợp A ∪ B và A ∩ B với: A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
 Xem đáp án
Xem đáp án
Vì mọi tam giác đều là tam giác cân nên tập A là tập hợp con của B.
Khi đó A ∪ B = B và A ∩ B = A.
Vậy A ∪ B = B và A ∩ B = A.
Câu 40:
Cho a, b, c > 0 thỏa mãn phương trình a + b + c = 3. Chứng minh rằng:
\[\frac{a}{{{b^2} + 1}} + \frac{b}{{{c^2} + 1}} + \frac{c}{{{a^2} + 1}} \ge \frac{3}{2}\].
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức Cô-si, ta có:
• \[\frac{a}{{{b^2} + 1}} = a - \frac{{a{b^2}}}{{{b^2} + 1}} \ge a - \frac{{a{b^2}}}{{2b}} = a - \frac{{a{b^2}}}{2}\];
• \[\frac{b}{{{c^2} + 1}} = b - \frac{{b{c^2}}}{{{c^2} + 1}} \ge b - \frac{{b{c^2}}}{{2c}} = b - \frac{{cb}}{2}\];
• \[\frac{c}{{{a^2} + 1}} = c - \frac{{c{a^2}}}{{{a^2} + 1}} \ge c - \frac{{c{a^2}}}{{2a}} = c - \frac{{ac}}{2}\].
Cộng ba vế bất đẳng thức lại ta được:
\[\frac{a}{{{b^2} + 1}} + \frac{b}{{{c^2} + 1}} + \frac{c}{{{a^2} + 1}} \ge a + b + c - \left( {\frac{{ab + bc + ac}}{2}} \right)\]
Ta có: \[ab + bc + ac \le \frac{{{{\left( {a + b + c} \right)}^2}}}{3} = \frac{9}{3} = 3\]
\[ \Rightarrow \frac{a}{{{b^2} + 1}} + \frac{b}{{{c^2} + 1}} + \frac{c}{{{a^2} + 1}} \ge 3 - \frac{3}{2} = \frac{3}{2}\]
Vậy \[\frac{a}{{{b^2} + 1}} + \frac{b}{{{c^2} + 1}} + \frac{c}{{{a^2} + 1}} \ge \frac{3}{2}\]
Câu 41:
Cho a + b + c = 0. Chứng minh a3 + b3 + c3 = 3abc.
 Xem đáp án
Xem đáp án
Từ giả thiết a + b + c = 0
Þ c = −(a + b), thay vào đẳng thức cần chứng minh ta được
a3 + b3 − (a + b)3 = −3ab(a + b)
Û −3ab2 − 3a2b = −3ab2 − 3a2b
Vậy a3 + b3 + c3 = 3abc.
Câu 42:
Cho A = (2; +¥), B = (m; +¥). Điều kiện cần và đủ của m sao cho B là tập con của A là.
 Xem đáp án
Xem đáp án
Ta có: B Ì A Û (m; +¥) Ì (2; +¥)
Do đó "x Î B
Þ x Î A
Þ m ³ 2.
Câu 43:
Tìm tập hợp A giao B biết A = (–1; +¥) và B = (1; 2).
 Xem đáp án
Xem đáp án
Ta có:
• A Ç B = {x Î ℝ | 1 < x < 2}.
• A È B = {x Î ℝ | x > –1}.Câu 44:
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm b sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh: ∆AOI = ∆BOI.
 Xem đáp án
Xem đáp án
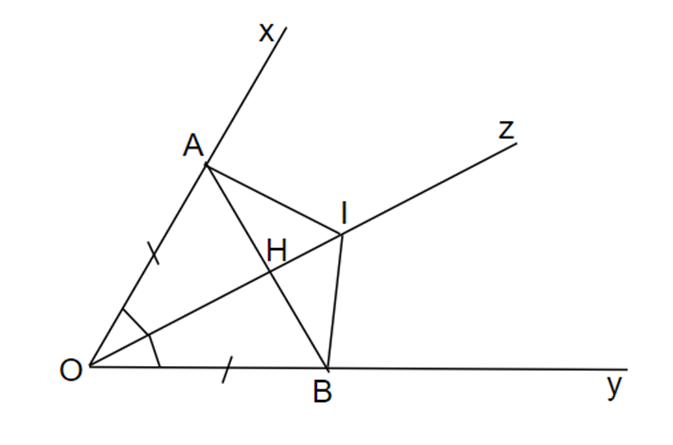
Vì Oz là phân giác của \[\widehat {xOy}\] nên \[\widehat {xOz} = \widehat {yOz} = \frac{1}{2}\widehat {xOy}\]
Xét ΔAOI và ΔBOI có:
OA = OB (gt)
\[\widehat {AOI} = \widehat {BOI}\] (cmt)
OI là cạnh chung
Do đó ΔAOI = ΔBOI (c.g.c)
Câu 45:
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm b sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh: AB vuông góc với OI.
 Xem đáp án
Xem đáp án
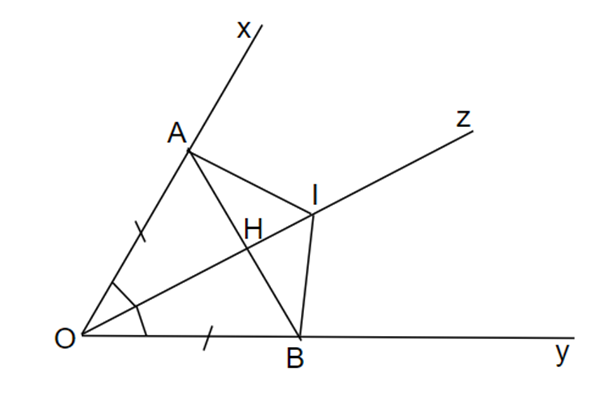
Xét Δ AOH và ΔBOH có:
OA = OB (gt)
\[\widehat {AOH} = \widehat {BOH}\]
OH là cạnh chung
Do đó ΔAOH = ΔBOH (c.g.c)
Suy ra \[\widehat {AHO} = \widehat {BHO}\] (hai góc tương ứng)
Mà \[\widehat {AHO} + \widehat {BHO} = 180^\circ \] (kề bù)
Nên \[\widehat {AHO} = \widehat {BHO} = 90^\circ \].
Do đó AB ⊥ OI.
Câu 46:
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A (1; −7 ); B (2; −8). Tính y (−1).
 Xem đáp án
Xem đáp án
Đồ thị hàm số đi qua A và B nên:
\[\left\{ \begin{array}{l}a + b + c + d = - 7\\8a + 4b + 2c + d = - 8\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}d = - 7 - a - b - c\\7a + 3b + c = - 1\end{array} \right.\] (1)
Ta có y ′ = 3ax2 + 2bx + c có 2 nghiệm x = 1 và x = 2 nên
\[\left\{ \begin{array}{l}3a + 2b + c = 0\,\,\,\,(2)\\12a + 4b + c = 0\,\,\,\,(3)\end{array} \right.\]
Từ (1), (2), (3) ta có a = 2; b = −9; c = 12 Þ d = −12
Khi đó y (−1) = −a + b − c + d = −35
Vậy y (−1) = −35.
Câu 47:
Cho hàm số y = ax3 + bx2 + cx + d. Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A (−1; −1) thì hàm số có phương trình là?
 Xem đáp án
Xem đáp án
Ta có: y’ = 3ax2 + 2bx + c
• Đồ thị hàm số có điểm cực trị là gốc tọa độ, ta có:
\[\left\{ \begin{array}{l}y'(0) = 0\\y(0) = 0\end{array} \right. \Leftrightarrow c = d = 0\]
• Đồ thị hàm số có điểm cực trị là A (–1; –1), ta có:
\[\left\{ \begin{array}{l}y'( - 1) = 0\\y( - 1) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a - 2b = 0\\b - a = - 1\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right.\]
Vậy hàm số là: y = –2x3 – 3x2.
Câu 48:
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M,N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB. Chứng minh: Tứ giác AMCN là hình bình hành.
 Xem đáp án
Xem đáp án
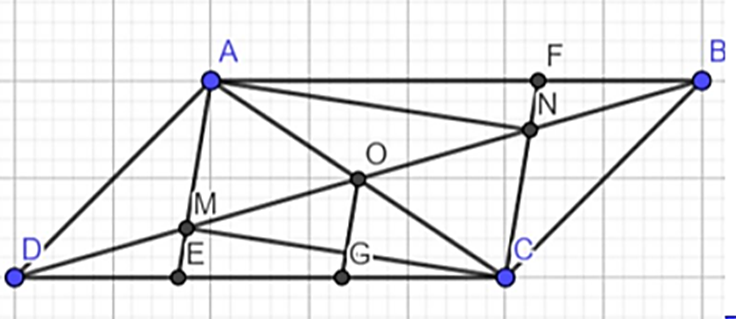
Ta có ABCD là hình bình hành
Þ AC Ç BD tại trung điểm của mỗi đường
Mà AC Ç BD = O
Þ O là trung điểm AC, DB
Lại có M, N là trung điểm OD, OB
\[ \Rightarrow OM = \frac{1}{2}OD = \frac{1}{2}OB = ON\]
Þ O là trung điểm MN
Do O là trung điểm của AC, MN
Þ AMCN là hình bình hành
Vậy AMCN là hình bình hành.
Câu 49:
Hình thang ABCD (AB // CD) có \[\widehat A - \widehat D = 20^\circ \], \[\widehat B = 2\widehat C\]. Tính các góc của hình thang.
 Xem đáp án
Xem đáp án
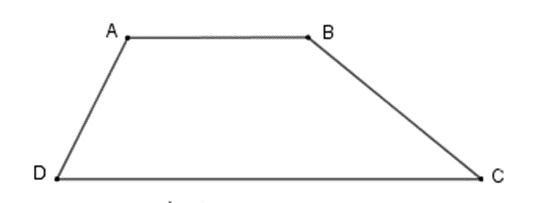
Ta có: \[\widehat A = 100^\circ ;\widehat B = 120^\circ ;\widehat C = 60^\circ ;\widehat D = 80^\circ \](2 góc kề tổng bằng 180°)
\[ \Rightarrow \left\{ \begin{array}{l}2\widehat A = 200^\circ \\A - D = 20^\circ \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat A = 100^\circ \\\widehat D = \widehat A - 20^\circ = 100^\circ - 20^\circ = 80^\circ \end{array} \right.\]
Lại có: \[\left\{ \begin{array}{l}\widehat B + \widehat C = {180^^\circ }\\\widehat B = 2\widehat C\end{array} \right.\](2 góc kề có tổng bằng 180°)
\[ \Rightarrow \left\{ \begin{array}{l}\widehat B = 2\widehat C\\2\widehat C + \widehat C = 180^\circ \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B = 2\widehat C\\3\widehat C = 180^\circ \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B = 120^\circ \\\widehat C = 60^\circ \end{array} \right.\]
Vậy \[\widehat A = 100^\circ ;\widehat B = 120^\circ ;\widehat C = 60^\circ ;\widehat D = 80^\circ \].
Câu 50:
Hình thang ABCD (AB // CD) có \[\widehat A - \widehat D = 20^\circ ,\widehat B = 2\widehat C\]. Tính các góc của hình thang.
 Xem đáp án
Xem đáp án
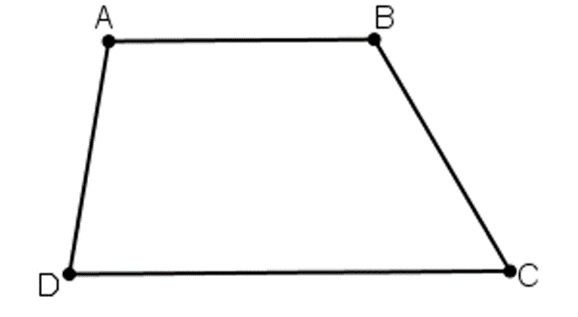
Ta có: \[\widehat A - \widehat D = 20^\circ \Rightarrow \widehat A = 20^\circ + \widehat D\]
AB // CD \[ \Rightarrow \widehat A + \widehat D = 180^\circ \]
(hai góc trong cùng phái bù nhau)
\[ \Rightarrow 20^\circ + \widehat D + \widehat D = 180^\circ \]
\[ \Rightarrow \widehat D = 80^\circ \]
\[ \Rightarrow \widehat A = \widehat D + 20^\circ \]
Lại có AB // CD \[ \Rightarrow \widehat B + \widehat C = 180^\circ \]
Mà \[\widehat B = 2\widehat C \Rightarrow 2\widehat C + \widehat C = 180^\circ \]
\[ \Rightarrow \widehat C = 60^\circ \]
\[ \Rightarrow \widehat B = 2\widehat C = 120^\circ \]
Vậy \[\widehat A = 100^\circ ;\widehat B = 120^\circ ;\widehat C = 60^\circ ;\widehat D = 80^\circ \].
Câu 51:
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC. Gọi E là giao điểm của AC và BD. Chứng minh tam giác AOB cân tại O.
 Xem đáp án
Xem đáp án
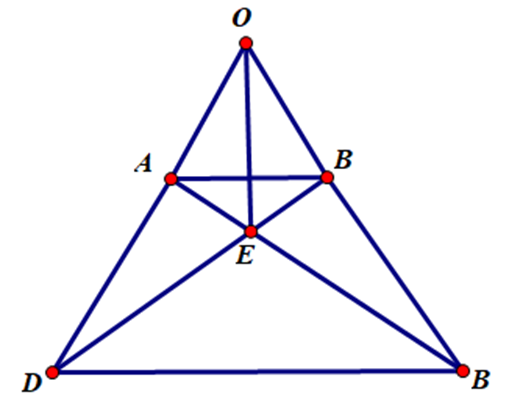
ABCD là hình thang cân
\[ \Rightarrow \widehat {BCD} = \widehat {ADC} \Leftrightarrow \widehat {OCD} = \widehat {ODC}\]
Þ ΔODC cân tại O
Þ OC = OD
Mà AD = BC (ABCD là hình thang cân)
Þ OA = OB
Vậy ΔOAB cân tại O.
ABCD là hình thang cân
\[ \Rightarrow \widehat {BCD} = \widehat {ADC} \Leftrightarrow \widehat {OCD} = \widehat {ODC}\]
Þ ΔODC cân tại O
Þ OC = OD
Mà AD = BC (ABCD là hình thang cân)
Þ OA = OB
Vậy ΔOAB cân tại O.
Câu 52:
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC. Gọi E là giao điểm của AC và BD. Chứng minh ΔABD = ΔBAC.
 Xem đáp án
Xem đáp án
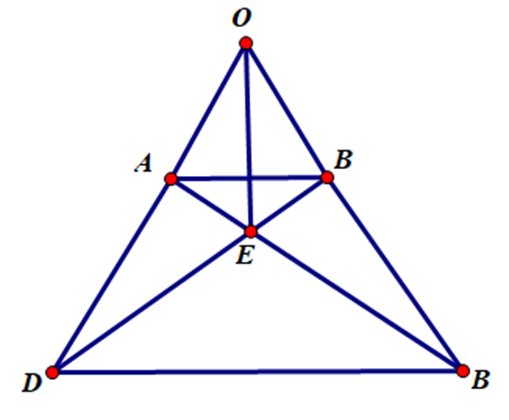
ABCD là hình thang cân
\[ \Rightarrow \widehat {BAD} = \widehat {ABC}\]
Xét ΔABD và ΔBAC có:
AB chung
AD = BC
\[\widehat {BAD} = \widehat {ABC}\]
Þ ΔABD = ΔBAC
Vậy ΔABD = ΔBAC.
Câu 53:
Cho hình thang cân ABCD, đáy nhỏ CD = a, tổng hai góc \[\widehat A;\widehat B\] bằng nửa tổng hai góc \[\widehat C;\widehat D\], đường chéo AC vuông góc với hai cạnh bên BC. Tính các góc hình thang ABCD.
 Xem đáp án
Xem đáp án
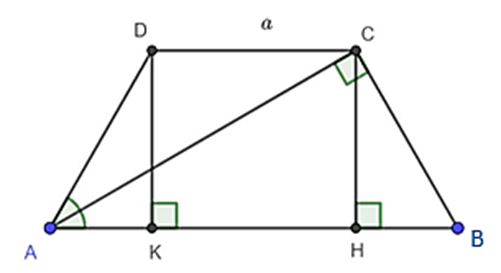
Theo đề ta có: \[\widehat A + \widehat B = \frac{1}{2}\left( {\widehat C + \widehat D} \right)\]
\[ \Rightarrow 2\widehat B = \frac{1}{2} \cdot 2\widehat C\] (do ABCD là hình thang cân) (1)
Mà \[\widehat B + \widehat C = 180^\circ \] (hai góc ở vị trí trong cùng phía) (2)
Từ (1) và (2) suy ra \[\widehat B + 2\widehat B = 180^\circ \]
\[ \Rightarrow \widehat B = 60^\circ \]
\[ \Rightarrow \widehat C = 120^\circ \]
Vậy \[\widehat A = \widehat B = 60^\circ \]; \[\widehat C = \widehat D = 120^\circ \].
Câu 54:
Cho hình thang cân ABCD, đáy nhỏ CD = a, tổng hai góc \[\widehat A;\widehat B\] bằng nửa tổng hai góc \[\widehat C;\widehat D\], đường chéo AC vuông góc với hai cạnh bên BC. Chứng minh AC là phân giác của \[\widehat {DAB}\].
 Xem đáp án
Xem đáp án
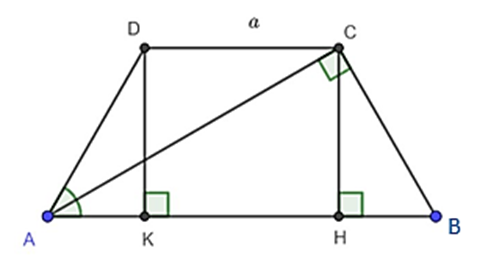
Theo đề ta có:
\[\widehat A + \widehat B = \frac{1}{2}\left( {\widehat C + \widehat D} \right)\]
\[ \Rightarrow 2\widehat B = \frac{1}{2} \cdot 2\widehat C\] (do ABCD là hình thang cân) (1)
Mà \[\widehat B + \widehat C = 180^\circ \] (hai góc ở vị trí trong cùng phía) (2)
Từ (1) và (2) suy ra \[\widehat B + 2\widehat B = 180^\circ \]
\[ \Rightarrow \widehat B = 60^\circ \]
Ta có: AC ^ BC
\[ \Rightarrow \widehat {ACB} = 90^\circ \]
\[ \Rightarrow \widehat {CAB} = 90^\circ - \widehat B = 90^\circ - 60^\circ = 30^\circ \]
Lại có:
\[\widehat {DAC} = \widehat A - \widehat {CAB} = 60^\circ - 30^\circ = 30^\circ \]
\[ \Rightarrow \widehat {DAC} = \widehat {CAB} = 30^\circ \]
Vậy AC là phân giác của \[\widehat {DAB}\].
Câu 55:
Cho hình thang vuông ABCD (\[\widehat A = \widehat D = 90^\circ \]). E là trung điểm của AD và \[\widehat {BEC} = 90^\circ \]. Cho biết AD = 2a. Chứng minh rằng: AB.CD = a².
 Xem đáp án
Xem đáp án
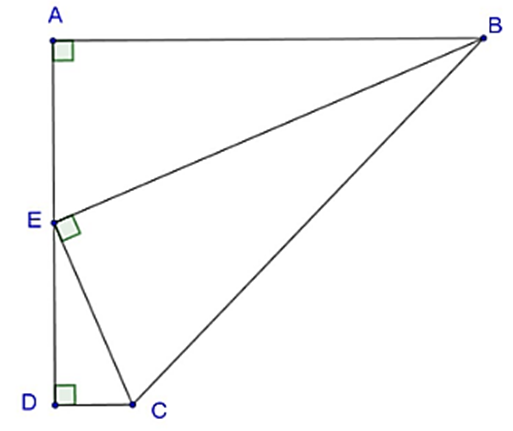
Xét ΔAEB và ΔDCE, ta có:
\[\widehat {EAB} = \widehat {CDE} = 90^\circ \]
\[\widehat {AEB} = \widehat {DCE}\] (cùng phụ \[\widehat {DEC}\])
Þ ΔAEB ᔕ ΔDCE (g.g)
\[ \Rightarrow \frac{{AB}}{{DE}} = \frac{{AE}}{{CD}}\]
Þ AB.CD = AE.DE = a2
Vậy AB.CD = a2 .
Câu 56:
Cho hình thang vuông ABCD (\[\widehat A = \widehat D = 90^\circ \]). E là trung điểm của AD và \[\widehat {BEC} = 90^\circ \]. Cho biết AD = 2a. Chứng minh rằng: ΔEAB đồng dạng ΔCEB.
 Xem đáp án
Xem đáp án

Xét ΔAEB và ΔDCE, ta có:
\[\widehat {EAB} = \widehat {CDE} = 90^\circ \]
\[\widehat {AEB} = \widehat {DCE}\] (cùng phụ \[\widehat {DEC}\])
Þ ΔEAB ᔕ ΔCDE (g.g)
\[ \Rightarrow \frac{{DE}}{{DC}} = \frac{{EB}}{{CE}} \Leftrightarrow \frac{{CE}}{{DC}} = \frac{{EB}}{{DE}}\]
Xét ΔCEB và ΔCDE, ta có:
\[\frac{{CE}}{{DC}} = \frac{{EB}}{{DE}}\]
\[\widehat {CEB} = \widehat {CDE} = 90^\circ \]
Þ ΔCEB ᔕ ΔCDE (c.g.c)
Mà ΔEAB ᔕ ΔCDE
Nên ΔEAB ᔕ ΔCEB
Vậy ΔEAB ᔕ ΔCEB.
Câu 57:
Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD, đường phân giác ngoài AE. Tính DB, EB.
 Xem đáp án
Xem đáp án
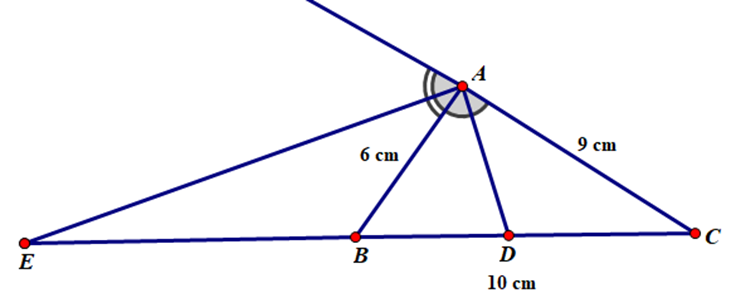
ΔABC có AD là đường phân giác
\[ \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\] (tính chất đường phân giác trong tam giác)
Þ 3DB = 2DC
Mà BD + CD = BC = 10
⇒ 2BD + 2CD = 20
⇒ 5BD = 20
⇒ BD = 4 (cm)
Lại có: ΔABC có AE là đường phân giác ngoài đỉnh A
\[ \Rightarrow \frac{{EB}}{{EC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\] (tính chất đường phân giác ngoài của tam giác)
Þ 3EB = 2EC
Mà EB + BC = EC
⇒ EB + 10 = EC
⇒ 2EB + 20 = 2EC
⇒ 2EB + 20 = 3EB
⇒ EB = 20 (cm)
Vậy DB = 4 cm và EB = 20 cm.
Câu 58:
Cho tam giác ABC có đường phân giác trong AD, đường phân giác ngoài AE. Chứng minh tam giác ADE vuông.
 Xem đáp án
Xem đáp án
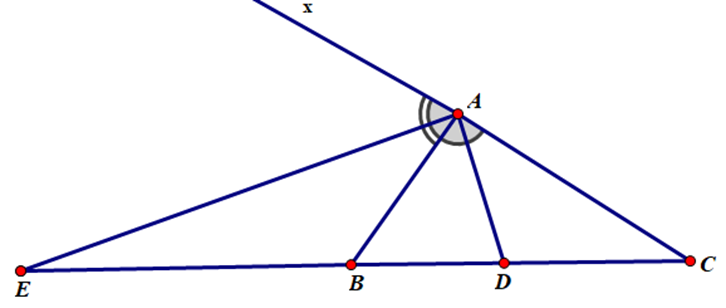
ΔABC có AD là đường phân giác trong
\[ \Rightarrow \widehat {BAD} = \frac{1}{2}\widehat {BAC}\]
AE là đường phân giác ngoài
\[ \Rightarrow \widehat {BAE} = \frac{1}{2}\widehat {BAx}\]
\[ \Rightarrow \widehat {BAD} + \widehat {BAE} = \frac{1}{2}\widehat {BAC} + \frac{1}{2}\widehat {BAx}\]
\[ \Rightarrow \widehat {DAE} = \frac{1}{2}\left( {\widehat {BAC} + \widehat {BAx}} \right)\]
\[ \Rightarrow \widehat {DAE} = \frac{1}{2} \cdot 180^\circ = 90^\circ \]
⇒ AD ⊥ AE
Vậy ΔADE vuông tại A.
Câu 59:
Cho tam giác ABC có a = 4; c = 5; B = 150°. Tính diện tích của tam giác.
 Xem đáp án
Xem đáp án
Áp dụng công thức tính diện tích tam giác, ta có:
\[{S_{ABC}} = \frac{1}{2}a.c.\sin B\]
\[\frac{1}{2}.4.5.\sin 150^\circ = 5\]
Vậy SABC = 5 đvdt.
Câu 60:
Tam giác ABC có AB = 5; BC = 7 và CA = 8. Tính số đo \[\widehat A\].
 Xem đáp án
Xem đáp án
Theo định lý hàm số cosin, ta có:
\[\cos \widehat A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\]
\[ \Leftrightarrow \cos \widehat A = \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}\]
\[ \Leftrightarrow \widehat A = 60^\circ \]
Vậy \[\widehat A = 60^\circ \].
Câu 61:
Cho tam giác ABC có AB = 12 cm, AC = 18 cm. Gọi M là chân đường vuông góc. Kẻ từ B đến tia phân giác \[\widehat A\]. Gọi M là trung điểm của IC. Tính HM.
 Xem đáp án
Xem đáp án
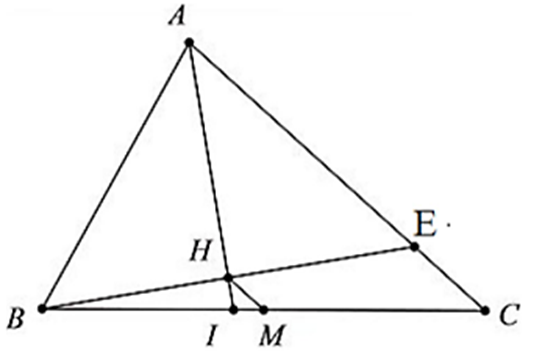
Gọi E là giao điểm của BH và AC
AD là tia phân giác góc A
AH là đường cao của ΔABE
AH là tia phân giác của góc BAE
Þ ᔕABE cân tại A
Þ AB = AE
Mà ta có: AB = 12 cm
Þ AE = 12 cm
EC = AC − AE = 18 − 12 = 6 cm
AH là đường cao của ΔABE cân tại A.
Þ AH là trung tuyến của ΔABE
Þ H là trung điểm của BE
Mà M là trung điểm của BC
Þ HM là đường trung bình của ΔBEC
\[ \Rightarrow HM = \frac{1}{2}EC = \frac{1}{2} \cdot 6 = 3\,\,\]
Vậy độ dài của HM = 3 cm.
Câu 62:
Cho tam giác ABC có AB = 14 cm, AC = 21 cm. AD là phân giác của \[\widehat A\]. Biết BD = 8 cm. Tính BC.
 Xem đáp án
Xem đáp án
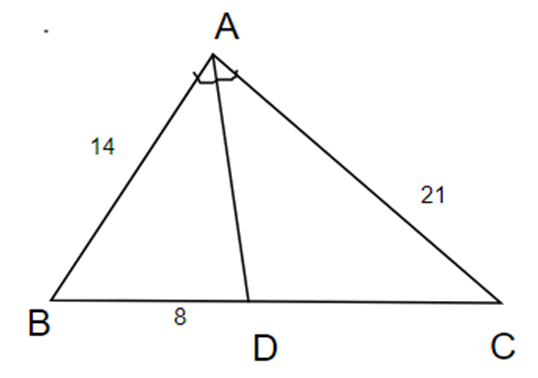
ΔABC có AD là tia phân giác của \[\widehat A\]
\[ \Rightarrow \frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\]
\[ \Rightarrow DC = \frac{{8.21}}{{14}} = 12\]
Ta có: BC = BD + DC = 8 + 12 = 20 (cm)
Vậy BC = 20 cm.
Câu 63:
Cho tam giác ABC thỏa mãn sin2 A = sin2 B + sin2 C. Chứng minh rằng tam giác ABC vuông. Biết AB = c; AC = b; BC = a.
 Xem đáp án
Xem đáp án
Áp dụng công thức:
\[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\]
Ta có: sin2 A = sin2 B + sin2 C
\[ \Leftrightarrow {\left( {\frac{a}{{2R}}} \right)^2} = {\left( {\frac{b}{{2R}}} \right)^2} = {\left( {\frac{c}{{2R}}} \right)^2}\]
Û a2 = b2 + c2
Vậy tam giác ABC vuông tại A.
Câu 64:
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm. Tính BC, AH.
 Xem đáp án
Xem đáp án
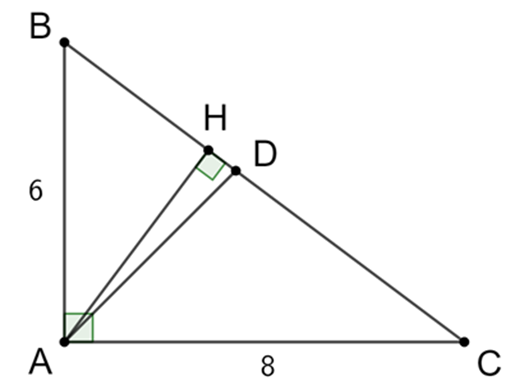
Vì ∆ABC vuông tại A nên ta có:
BC2 = AB2 + AC2
Þ BC2 = 62 + 82 = 100
Þ BC = 10 cm
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\]
\[ \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{1}{{{6^2}}} + \frac{1}{{{8^2}}} = \frac{{25}}{{576}}\]
\[ \Leftrightarrow AH = \frac{{24}}{5} = 4,8\] (cm)
Vậy BC = 10 cm, AH = 4,8 cm.
Câu 65:
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm. Tính BH, CH.
 Xem đáp án
Xem đáp án
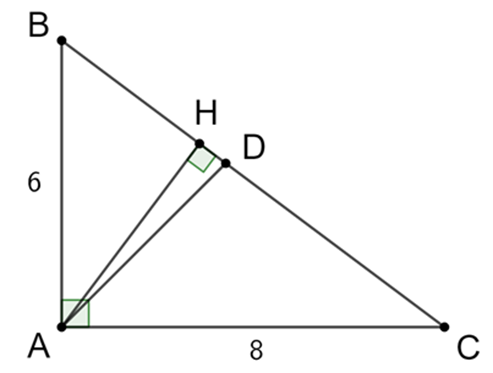
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
AB2 = BA.BC
Û 62 = BH.10
Û BH = 3,6 cm
Þ HC = BC − BH = 10 − 3,6 = 6,4 (cm)
Vậy BH = 3,6 cm, HC = 6,4 cm.
Câu 66:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB và O là 1 điểm tùy ý. Chứng minh rằng: \[\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \].
 Xem đáp án
Xem đáp án
Ta có trong ΔABC có M là trung điểm của BC và N là trung điểm của AC
Þ PM là đường trung bình của ΔABC
Þ PM // AB và \[PM = \frac{1}{2}AB = NC\]
\[\overrightarrow {PM} = \overrightarrow {NC} \]
Ta có:
• \[\overrightarrow {AM} = \overrightarrow {AP} + \overrightarrow {PM} \]
• \[\overrightarrow {BN} = \overrightarrow {BP} + \overrightarrow {PN} \]
• \[\overrightarrow {CP} = \overrightarrow {CN} + \overrightarrow {NP} \]
\[\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow {AP} + \overrightarrow {PM} + \overrightarrow {BP} + \overrightarrow {PN} + \overrightarrow {CN} + \overrightarrow {NP} \]
\[ = \overrightarrow {AP} + \overrightarrow {BP} + \overrightarrow {PM} + \overrightarrow {CN} \]
\[ = - \left( {\overrightarrow {PA} + \overrightarrow {PB} } \right) + \overrightarrow {CN} + \overrightarrow {NC} \]\[ = \overrightarrow 0 \]
Vậy \[\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \].
Câu 67:
Cho ∆ABC cân tại A có M là trung điểm BC, đường cao CN cắt AM tại H. Chứng minh BH ^ AC.
 Xem đáp án
Xem đáp án
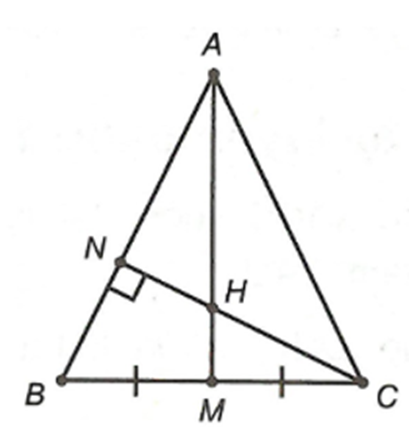
• Xét ∆ABC cân tại A có AM là đường trung tuyến nên M là trung điểm của BC.
• Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (do ∆ABC cân tại A)
BM = CM (do M là trung điểm BC)
Do đó ∆ABM = ∆ACM (c.c.c)
\[ \Rightarrow \widehat {AMB} = \widehat {AMC}\]
Mà \[\widehat {AMB} + \widehat {AMC} = 180^\circ \]
\[\widehat {AMB} = \widehat {AMC} = 90^\circ \]
Do đó AM ^ BC.
∆ABC có AM, CN là hai đường cao.
Mà H là giao điểm của AM và CN.
Do đó H là trực tâm của ∆ABC.
Vậy BH ⊥ AC.
Câu 68:
Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC lấy D sao cho MD = MC. Trên tia đối của tia NB lấy điểm E sao cho NE = NB. Chứng minh △AMD = △BMC.
 Xem đáp án
Xem đáp án
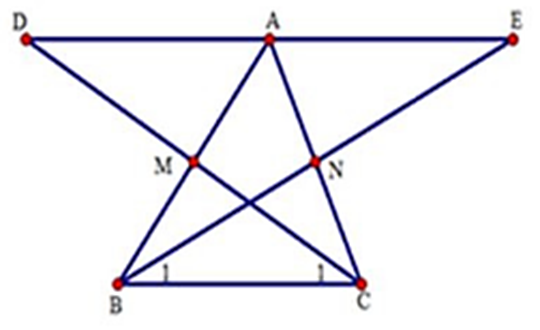
Xét ΔAMD và ΔBMC có:
DM = MC (gt)
\[\widehat {BMC} = \widehat {AMD}\] (hai góc đối đỉnh)
AM = BM (gt)
Þ ΔAMD = ΔBMC (c.g.c)
Vậy ΔAMD = ΔBMC.
Câu 69:
Cho tập hợp A={0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Số tự nhiên thỏa mãn có dạng \[\;\overline {abcd} \] với a, b, c, d ∈ A và đôi một khác nhau.
Trường hợp 1: d = 0
Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có 5.4.3 = 60 số.
Trường hợp 2: d ≠ 0 ; d có 2 cách chọn là 2, 4
Khi đó có 4 cách chọn a (vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.
Theo quy tắc nhân có: 2.4.4.3 = 96 số
Có tất cả số số là: 96 + 60 = 156 (số)
Vậy có 156 số.
Câu 70:
Cho tập hợp A = 0; 1; 2; 3; 4; 5; 6; 7. Hỏi từ tập A có thể lập được bao nhiêu chữ số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên phải bằng 1?
 Xem đáp án
Xem đáp án
Gọi số đó là a b c d e
Trường hợp 1: a = 1
+ b có 7 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 7.6.5.4 = 840 số
Trường hợp 2:b = 1
+ a ≠ b , a ≠ 0 nên có 6 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 6.6.5.4 = 720 số
Trường hợp 3: c = 1.
+ a ≠ c , a ≠ 0 nên có 6 cách chọn.
+ b có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có 6.6.5.4=720 số
Có tất cả số số là: 840 + 720 + 720 = 2280 (số)
Vậy có 2280 số.
Câu 71:
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A đến B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng. CE = CF.
 Xem đáp án
Xem đáp án
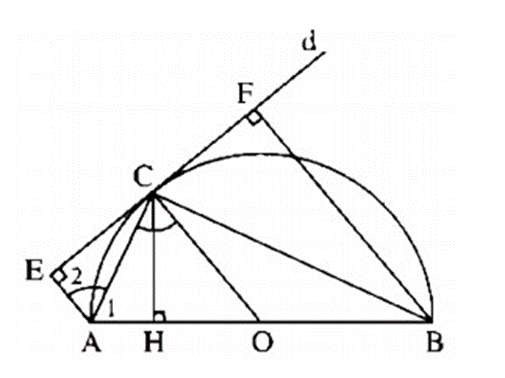
Ta có: OC ⊥ d ( tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra: OC // AE // BF
Mà OA = OB (=R)
Suy ra: CE = CF (tính chất đường thẳng song cách đều)
Vậy CE = CF
Câu 72:
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A đến B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng AC là tia phân giác của góc \[\widehat {BAE}\].
 Xem đáp án
Xem đáp án
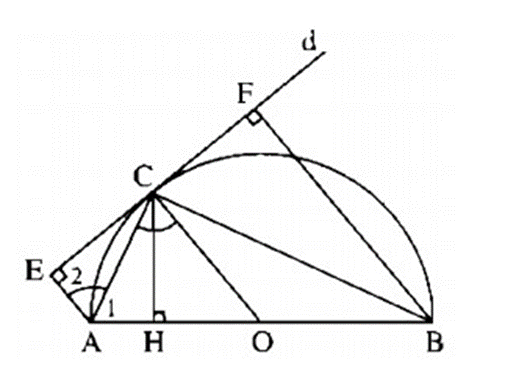
Ta có: AE // OC
Suy ra: \[\widehat {OCA} = \widehat {EAC}\] ( hai góc sole trong) (1)
Ta có: OA = OC (= R)
Suy ra: ∆OAC cân tại O
Þ \[\widehat {OCA} = \widehat {OAC}\](2)
Từ (1) và (2) suy ra: \[\widehat {EAC} = \widehat {OAC}\]
Þ AC là tia phân giác của góc OAE
Vậy AC là tia phân giác của \[\widehat {BAE}\].
Câu 73:
 Xem đáp án
Xem đáp án
Ta có:
a(b.cos C – c.cos B)
\[ = ab.\frac{{{b^2} + {a^2} - {c^2}}}{{2ab}} - ac.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\]
\[ = \frac{1}{2}\left( {{b^2} + {a^2} - {c^2} - {a^2} - {c^2} + {b^2}} \right)\]
= b2 – c2
Vậy b2 – c2 = a(b.cos C – c.cos B).
Câu 74:
Trong tam giác ABC có độ dài các cạnh BC = a; AC = b; AB = c. Chứng minh: (b2 – c2).cos A = a(c.cos C – b.cos B)
 Xem đáp án
Xem đáp án
Ta có: a(c.cos C – b.cos B) = accosC – abcosB
\[ = ac.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} - ab.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\]
\[ = c.\frac{{{a^2} + {b^2} - {c^2}}}{{2b}} - b.\frac{{{a^2} + {c^2} - {b^2}}}{{2c}}\]
\[ = \frac{{{a^2}{c^2} + {c^2}{b^2} - {c^4} - {b^2}{a^2} - {b^2}{c^2} + {b^4}}}{{2bc}}\]
\[ = \frac{{{b^2}\left( {{b^2} + {c^2} - {a^2}} \right) - {c^2}\left( {{b^2} + {c^2} - {a^2}} \right)}}{{2bc}}\]
\[ = \left( {{b^2} - {c^2}} \right)\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\]
\[ = \left( {{b^2} - {c^2}} \right)\cos A\]
Vậy (b2 – c2).cos A = a(c.cos C – b.cos B)
Câu 75:
Chứng minh \[1 + tanx + ta{n^2}x + ta{n^3}x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}{{{{\cos }^3}x}}\].
 Xem đáp án
Xem đáp án
\[1 + tanx + ta{n^2}x + ta{n^3}x\]
\[8:\frac{5}{4} \times \frac{5}{4} = 8\]
\[ = \frac{{{{\cos }^3}x + {\mathop{\rm s}\nolimits} {\rm{inx}}.{{\cos }^2}x + {\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{x}}.\cos x + {\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^3}{\rm{x}}}}{{{{\cos }^3}x}}\]
\[ = \frac{{{{\cos }^2}x.({\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x) + {\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{x}}.({\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x)}}{{{{\cos }^3}x}}\]
Vậy \[1 + tanx + ta{n^2}x + ta{n^3}x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}{{{{\cos }^3}x}}\].
Câu 76:
Chứng minh đẳng thức: (1 + sin x)(cot x – cos x) = cos3 x.
 Xem đáp án
Xem đáp án
\[\left( {1 + sinx} \right)\left( {\cot x--cosx} \right)\]
\[ = (1 + \sin x)(\frac{{\cos x}}{{\sin x}} - \cos x)\]
\[ = \cos x(1 + \sin x).\frac{{1 - \sin x}}{{\sin x}}\]
\[ = \frac{{\cos x(1 - {{\sin }^2}x)}}{{\sin x}} = \frac{{\cos x.{{\cos }^2}x}}{{\sin x}} = \frac{{{{\cos }^3}x}}{{\sin x}}\]
Vậy (1 + sin x)(cot x – cos x) = cos3 x.
Câu 77:
Mẹ Lan gửi tiết kiệm 100 triệu đồng với lãi suất 0,7% một năm. Sau 1 năm mẹ lan nhận được cả vốn và lãi là bao nhiêu tiền?
 Xem đáp án
Xem đáp án
100 triệu = 100 000 000 đồng
Số tiền lãi của mẹ Lan sau 1 năm là:
100 000 000 × 0,7 : 100 = 700 000 (đồng)
Số tiền gốc và lãi của mẹ Lan là:
100 000 000 + 700 000 = 100 700 000 (đồng)
Đáp số: 100 700 000 đồngCâu 78:
Mẹ bạn hân gửi 100 triệu đồng vào ngân hàng theo hình thức có kì hạn 12 tháng với lãi suất 6% một năm. Hỏi sau một năm mẹ bạn hân nhận được bao nhiêu tiền lãi?
 Xem đáp án
Xem đáp án
Sau một năm mẹ bạn Hân nhận tổng cộng số phần trăm là:
100% + 6% = 106%
100 triệu = 100 000 000 đồng
Sau một năm mẹ bạn Hân nhận được số tiền là:
100 000 000 × 106 : 100 = 106 000 000 (đồng)
Số tiền lãi mẹ Hân nhận được số tiền là:
106 000 000 – 100 000 000 = 6 000 000 (đồng)
Đáp số: 6 000 000 đồng.
Câu 79:
Chứng minh rằng 1 số chính phương có số ước là 1 số lẻ.
 Xem đáp án
Xem đáp án
Gọi P là một số chính phương.
Ta có: P = k2 (\[k \in \mathbb{N}\])
Giả sử k phân tích ra thừa số nguyên tố là k = ax.by.cz.... (a, b, c là các số nguyên tố)
Þ P = (ax.by.cz....)2
Þ P = a2x.b2y.c2z
Vì 2 chia hết cho 2 nên 2x, 2y, 2z, ... cũng chia hết cho 2
Þ 2x, 2y, 2z, ... là số chẵn
Số lượng ước của P là (2x + 1)(2y + 1)(2z + 1)...
Vì 2x, 2y, 2z, ... là số chẵn nên 2x + 1, 2y + 1, 2z + 1, ... là số lẻ
Þ (2x + 1)(2y + 1)(2z + 1)... là số lẻ
Þ Số lượng ước của P là 1 số lẻ
Vậy số chính phương luôn có số ước là 1 số lẻ.
Câu 80:
Một đội 10 người trong một ngày đào được 35 m nương. Người ta bổ sung thêm 20 người nữa cùng đào thì trong một ngày đào được bao nhiêu mét mương? (Mức đào của mỗi người như nhau).
 Xem đáp án
Xem đáp án
Trong một ngày 20 người đào được số mét là:
35 × 20 : 10 = 70 (m)
Trong một ngày cả đội đó đào được số mét là:
35 + 70 = 105 (m)
Đáp số: 105 m mương.
Câu 81:
Một đội công nhân gồm 8 người được giao đắp một đoạn mương trong 20 ngày. Sau khi đắp được 5 ngày, đội đó được bổ sung thêm 16 người về cùng làm. Hỏi đơn vị đó đắp xong đoạn mương được giao trong bao nhiêu ngày? Biết rằng năng suất làm việc của mọi người trong một ngày là như nhau.
 Xem đáp án
Xem đáp án
Thời gian để đội công nhân đó làm xong công việc còn lại là:
20 − 5 = 15 (ngày)
Số người của đội đó sau khi được bổ sung thêm là:
8 + 16 = 24 (người)
Thời gian để 1 người làm xong công việc còn lại là:
15 × 8 =120 (ngày)
Thời gian để đội công nhân đó sau khi bổ sung thêm người hoàn thành công việc còn lại là:
120 : 24 = 5 (ngày)
Thời gian để đội công nhân hoàn thành toàn bộ công việc được giao là:
5 + 5 =10 (ngày)
Đáp số: 10 ngày.
Câu 82:
Một đội công nhân có 120 người được giao đắp một đoạn đường dài 4 km mỗi ngày phải làm việc 8 giờ. Trước khi khởi công, đội được điều thêm 30 người về làm và được giao đắp thêm 1 km đường nữa. Hỏi để hoàn thành đúng kế hoạch thì mỗi ngày phải làm việc mấy giờ?
 Xem đáp án
Xem đáp án
Tổng số công nhân sau khi điều thêm là:
120 + 30 = 150 (người)
Đoạn đường đội công nhân đắp dài là:
4 + 1 = 5 (km)
150 công nhân gấp 120 công nhân số lần là:
\[150:120 = \frac{5}{4}\] (lần)
5 km gấp 4 km số lần là :
\[5:4 = \frac{5}{4}\] (lần)
Để hoàn thành đúng kế hoạch thì mỗi ngày phải làm việc là:
\[8:\frac{5}{4} \times \frac{5}{4} = 8\](giờ)
Đáp số: 8 giờ
Câu 83:
Một đội công nhân có 40 người được giao nhiệm vụ hoàn thành một công việc trong 15 ngày. Sau khi làm được 3 ngày thì 20 công nhân được điều đi nơi khác. Hỏi đội công nhân đó hoàn thành công việc được giao trong bao nhiêu ngày? Biết rằng năng suất làm việc của mỗi người là như nhau.
 Xem đáp án
Xem đáp án
1 ngày cần số người là:
40 × 15 = 600 (người)
3 ngày cần số người là:
40 × 3 = 120 (người)
Đội công nhân đó hoàn thành công việc được giao trong số ngày là:
(600 − 120) : (40 − 20) = 24 (ngày)
Đáp số: 24 ngày.
