Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự D, E. Chứng minh rằng DE = BD + CE.
Giải bởi Vietjack
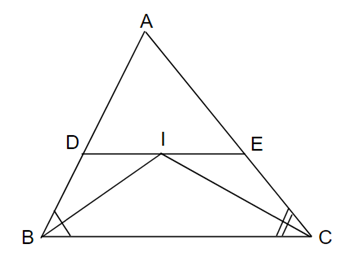
Ta có: BI là tia phân giác \[\widehat B\]\[ \Rightarrow \widehat {DBI} = \widehat {IBC}\]
Mà \[\widehat {DIB} = \widehat {IBC}\] (2 góc so le trong do DE // BC)
\[ \Rightarrow \widehat {DIB} = \widehat {DBI}\]⇒ ∆ DBI cân tại D.
⇒ BD = DI.
Ta có: CI là phân giác \[\widehat C\] \[ \Rightarrow \widehat {ECI} = \widehat {ICB}\]
Mà \[\widehat {EIC} = \widehat {ICB}\] (2 góc so le trong do DE // BC)
\[ \Rightarrow \widehat {ECI} = \widehat {EIC}\] ⇒ ∆CEI cân tại E.
⇒ CE = IE.
Ta có: BD = DI; CE = IE
⇒ BD + CE = DI + IE
Hay BD + CE = DE.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Với giá trị nào của x thì đa thức dư trong mỗi phép chia sau có giá trị bằng: (x5 + 2x4 + 3x4 + x ‒ 3) : (x2 + 1)
Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?
Cho hàm số \[y = f\left( x \right) = \frac{{3x + 1}}{{1 - x}}\] (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a, CD = a . Góc giữa 2 mặt phẳng (SBC) và (ABCD) bằng 60° .Gọi I là trung điểm của cạnh AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt đáy. Tính thể tích khối chóp SABCD theo a.
Cho nửa đường tròn (O; R) đường kính BC và một điểm A trên nửa đường tròn (A khác B, C). Hạ AH vuông góc BC tại H. Trên nửa mp bờ BC chứa A dựng 2 nửa đường tròn đường kính HB, HC chúng lần lượt cắt AB, AC tại E và F. Chứng minh AE.AB = AF.AC.\[\]
Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.
Có bao nhiêu số tự nhiên có 10 chữ số đôi một khác nhau, trong đó các chữ số 1, 2, 3, 4, 5 được xếp theo thứ tự tăng dần từ trái qua phải và chữ số 6 luôn đứng trước chữ số 5.
Cho tam giác ABC vuông cân tại A, \[AB = \sqrt 2 \]. Về phía ngoài tam giác vẽ tam giác ACD vuông cân tại D .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính diện tích ABCD.
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
a) Tam giác IMN cân tại I.
b) OI là đường trung trực của MN.
Tính giá trị lớn nhất của diện tích một tam giác biết 3 trong 2 cạnh của nó là 5 và 8.
Tìm một số có hai chữ số, biết rằng nếu viết chữ số 0 xen giữa hai chữ số của số đó thì được một số có ba chữ số, gấp 9 lần số ban đầu. Tìm số đã cho.
Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.
