Để tính theo phương pháp tích phân từng phần, ta đặt:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
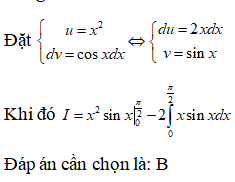
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho là hai hàm số có đạo hàm liên tục trên đoạn và thỏa mãn điều kiện . Tính tích phân
Hàm số có nguyên hàm trên đồng thời thỏa mãn . Lựa chọn phương án đúng:
Cho hàm số liên tục trên . Giả sử hàm số có đạo hàm liên tục trên và hơn nữa liên tục trên đoạn . Mệnh đề nào sau đây là đúng?