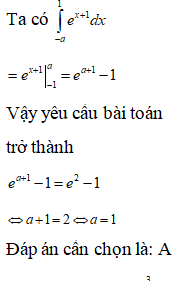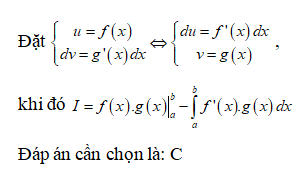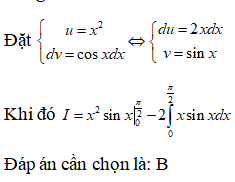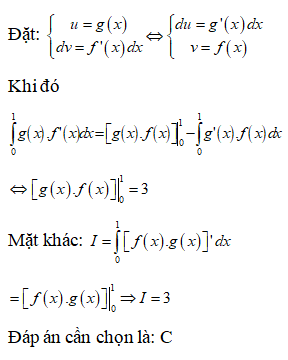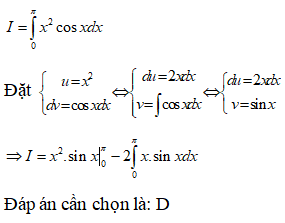14 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích phân có đáp án (Nhận biết)

Câu 1:

Cho số thực a thỏa mãn $\int_{- a}^{1} e^{x + 1} d x = e^{2} - 1$ , khi đó a có giá trị bằng

A.1

B. -1

C. 0

D. 2

Xem đáp án

Câu 2:

Tích phân $\int_{1}^{3} e^{x} d x$ bằng:

A. $e^{- 2}$

B. $e^{3} - e$

C. $e - e^{3}$

D. $e^{2}$

Xem đáp án

Ta có: $\int_{1}^{3} e^{x} d x = {e^{x}}_{1}^{3} = e^{3} - e$

Đáp án cần chọn là: B

Câu 3:

Tích phân $I = \int_{2}^{5} \frac{d x}{x}$ có giá trị bằng:

A. $3 \ln (3)$

B. $\frac{1}{3} \ln (3)$

C. $\ln (\frac{5}{2})$

D. $\ln (\frac{2}{5})$

Xem đáp án

$I = \int_{2}^{5} \frac{d x}{x} = \ln {|x|}_{2}^{5} = \ln (5) - \ln (2) = \ln (\frac{5}{2})$

Đáp án cần chọn là: C

Câu 4:

Hàm số $y = f (x)$ có nguyên hàm trên $(a; b)$ đồng thời thỏa mãn $f (a) = f (b)$ . Lựa chọn phương án đúng:

A. $\int_{a}^{b} f' (x) . e^{f x} d x = 0$

B. $\int_{a}^{b} f' (x) . e^{f x} d x = 1$

C. $\int_{a}^{b} f' (x) . e^{f x} d x = - 1$

D. $\int_{a}^{b} f' (x) . e^{f x} d x = 2$

Xem đáp án

Đặt $t = f (x) \Rightarrow d t = f' (x) d x$

Đổi cận $\{\begin{cases} x = a \Rightarrow t = f (a) \\ x = b \Rightarrow t = f (b) \end{cases}$

Khi đó $I = \int_{f (a)}^{f (b)} e^{t} d t = 0$ (Vì $f (a) = f (b))$

Đáp án cần chọn là: A

Câu 5:

Cho hàm số $y = f (x)$ liên tục trên $[a; b]$ . Giả sử hàm số $u = u (x)$ có đạo hàm liên tục trên $[a; b]$ và $u (x) \in [α; β]$ $\forall x \in [a; b]$ hơn nữa liên tục trên đoạn $[a; b]$ . Mệnh đề nào sau đây là đúng?

A. $\int_{a}^{b} f (u (x)) u' (x) d x = \int_{u (a)}^{u (b)} f (u) d u$

B. $\int_{a}^{b} f (u (x)) u' (x) d x = \int_{a}^{b} f (u) d u$

C. $\int_{u (a)}^{u (b)} f (u (x)) u' (x) d x = \int_{a}^{b} f (u) d u$

D. $\int_{a}^{b} f (u (x)) u' (x) d x = \int_{a}^{b} f (u) d u$

Xem đáp án

Đặt $t = u (x) \Rightarrow d t = u' (x) d x$ . Đổi cận $\{\begin{cases} x = a \to t = u (a) \\ x = b \to t = u (b) \end{cases}$

$\Rightarrow \int_{a}^{b} f (u (x)) . u' (x) d x = \int_{u (a)}^{u (b)} f (t) d t = \int_{u (a)}^{u (b)} f (u) d u$

Đáp án cần chọn là: A

Câu 6:

Cho $\int_{0}^{4} f (x) d x = - 1$ , tính $\int_{0}^{1} f (4 x) d x$

A. $I = \frac{- 1}{2}$

B. $I = \frac{- 1}{4}$

C. $I = \frac{1}{4}$

D. $I = - 2$

Xem đáp án

Đặt $4 x = t$ khi đó $4 d x = d t$

Đổi cận với $x = 0$ thì $t = 0; x = 1$ thì $t = 4$

$\int_{0}^{1} f (4 x) d x = \frac{1}{4} \int_{0}^{4} f (t) d t = \frac{- 1}{4}$ vì tích phân không phụ thuộc vào biến số

Đáp án cần chọn là: B

Câu 7:

Cho tích phân $I = \int_{a}^{b} f (x) . g' (x) d x$ , nếu đặt $\{\begin{cases} u = f (x) \\ d v = g' (x) d x \end{cases}$ thì:

A. $I = f (x) . {g' (x)}_{a}^{b} - \int_{a}^{b} f' (x) . g x d x$

B. $I = f (x) . {g (x)}_{a}^{b} - \int_{a}^{b} f (x) . g (x) d x$

C. $I = f (x) . {g (x)}_{a}^{b} - \int_{a}^{b} f' (x) . g (x) d x$

D. $I = f (x) . {g' (x)}_{a}^{b} - \int_{a}^{b} f (x) . g' (x) d x$

Xem đáp án

Câu 8:

Để tính $I = \int_{0}^{\frac{π}{2}} x^{2} \cos x d x$ theo phương pháp tích phân từng phần, ta đặt:

A. $\{\begin{cases} u = x \\ d v = x \cos x d x \end{cases}$

B. $\{\begin{cases} u = x^{2} \\ d v = \cos x d x \end{cases}$

C. $\{\begin{cases} u = \cos x \\ d v = x^{2} d x \end{cases}$

D. $\{\begin{cases} u = x^{2} \cos x \\ d v = d x \end{cases}$

Xem đáp án

Câu 9:

Cho $f (x), g (x)$ là hai hàm số có đạo hàm liên tục trên đoạn $[0; 1]$ và thỏa mãn điều kiện $\int_{0}^{1} g (x) . f' (x) d x = 1, \int_{0}^{1} g' (x) . f (x) d x = 2$ . Tính tích phân $I = \int_{0}^{1} [f (x) . g (x)]' d x$