Cho điểm A(1; 1) và hai đường thẳng (d₁): y = x − 1; (d₂): y = 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d₁), (d₂) tạo thành một tam giác vuông.

Đồ thị sau đây biểu diễn hàm số nào?

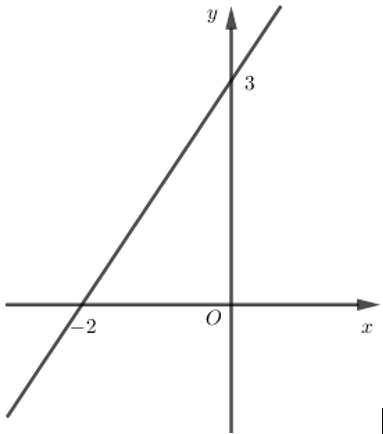
Cho hàm số y = ax + b có đồ thị là hình bên. Giá trị của a và b là:

Tìm giá trị thực của tham số m để ba đường thẳng y = −5(x + 1), y = mx + 3 và y = 3x + m phân biệt và đồng qui.

Biết rằng đồ thị hàm số y = ax + b đi qua điểm E (2; −1) và song song với đường thẳng ON với O là gốc tọa độ và N (1; 3). Tính giá trị biểu thức S = a² + b².

Tìm phương trình đường thẳng d: y = ax + b. Biết đường thẳng d đi qua điểm I (1; 2) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 4.

Hàm số y = |x − 5| có đồ thị nào trong các đồ thị sau đây?

Hàm số y = 2x − 1 có đồ thị là hình nào trong bốn hình sau?

Cho đường thẳng (d): y = –2x + 3. Tìm m để đường thẳng d′: y = mx + 1 cắt d tại một điểm thuộc đường phân giác của góc phần tư thứ hai

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017] để hàm số y = (m² − 4)x + 2m đồng biến trên R.

Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).

Xét các mệnh đề:

i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn

ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn

iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ

Số mệnh đề đúng là:

Tìm m để hàm số y = − (m² + 1)x + m − 4 nghịch biến trên R.

Hàm số y = 2x −$\frac{3}{2}$  có đồ thị là hình nào trong bốn hình sau

Tìm điểm cố định thuộc đồ thị hàm số y = 2mx – m + 1 (d)

Hàm số y = |x| + 2 có bảng biến thiên nào sau đây?

Cho hai đường thẳng (d1): y = −3x + m + 2; (d2): y = 4x − 2m − 5. Gọi A (1; y_A) thuộc (d1), B (2; y_B) thuộc (d2). Tìm tất cả các giá trị của m để A và B nằm về hai phía của trục hoành.