Diện tích của hình phẳng giới hạn bởi các đường $y=co{s}^{2}x,y=0,x=0,x=\frac{\mathrm{\pi }}{4}$ bằng

I. Tính diện tích hình phẳng

1. Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: $S=\underset{a}{\overset{b}{\int }}|f\left(x\right)|𝑑x$.

Ví dụ 1. Tính diện tích hình phẳng được giới hạn bởi y = 5x⁴ + 3x², trục hoành và hai đường thẳng x = 0; x = 1.

Lời giải:

Diện tích hình phẳng cần tính là:

$\begin{array}{c}S=\underset{0}{\overset{1}{\int }}|\mathrm{\hspace{0.17em}\hspace{0.17em}5}{x}^4+\mathrm{\hspace{0.17em}3}{x}^2|𝑑x=\underset{0}{\overset{1}{\int }}(5x^4+\mathrm{\hspace{0.17em}3}{x}^2)𝑑x={(x^5+x^3)|}_0^1=\mathrm{\hspace{0.17em}2}\end{array}$

2. Hình phẳng được giới hạn bởi 2 đường cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:

$S=\underset{a}{\overset{b}{\int }}|f\left(x\right)-g\left(x\right)|𝑑x$  (*).

- Chú ý.

Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].

Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:

$\underset{a}{\overset{c}{\int }}|f\left(x\right)-g\left(x\right)|𝑑x=|\underset{a}{\overset{c}{\int }}[f\left(x\right)-g\left(x\right)]𝑑x|$.

Ví dụ 2. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x² – 1.

Lời giải:

Phương trình hoành độ giao điểm của hai đường cong:

x – 1 = x² – 1

$\iff x-x^2=\mathrm{\hspace{0.17em}\hspace{0.17em}0}\iff [\begin{array}{c}x=0\\ x=\mathrm{\hspace{0.17em}1}\in [0;\mathrm{\hspace{0.17em}2}]\end{array}$

Diện tích hình phẳng đã cho là:

$\begin{array}{c}S=\underset{0}{\overset{2}{\int }}|x-1-(x^2-1)|𝑑x=\underset{0}{\overset{2}{\int }}|x-x^2|𝑑x=\underset{0}{\overset{1}{\int }}|x-x^2|𝑑x+\underset{1}{\overset{2}{\int }}|x-x^2|𝑑x\end{array}$

$\begin{array}{c}=|\underset{0}{\overset{1}{\int }}(x-x^2)𝑑x|+|\underset{1}{\overset{2}{\int }}(x-x^2)𝑑x|={\left|(\frac{x^2}{2}-\frac{x^3}{3})\right|}_0^1|+{\left|(\frac{x^2}{2}-\frac{x^3}{3})\right|}_1^2|\end{array}$

$=\frac{1}{6}+|\frac{-2}{3}-\frac{1}{6}|=\mathrm{\hspace{0.17em}1}$.

II. Tính thể tích

1. Thể tích của vật thể

Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm x $(a\le x\le b)$ cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].

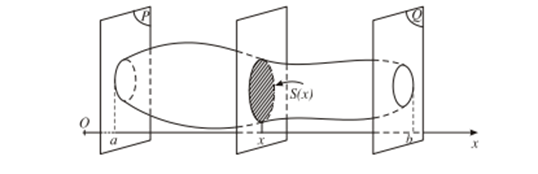
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức: $V=\underset{a}{\overset{b}{\int }}S\left(x\right)𝑑x.$

2. Thể tích khối chóp và khối chóp cụt.

a) Cho khối chóp có diện tích đáy là B, chiều cao h.

Khi đó, thể tích của khối chóp là $V=\frac{1}{3}B.h.$

b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.

Thể tích của khối chóp cụt là:

$V=\frac{h}{3}(B+\sqrt{B.B^{\text{'}}}+B^{\text{'}})$

III. Thể tích khối tròn xoay

 - Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong  y = f(x), trục hoành và hai đường thẳng x = a;  x = b quanh trục Ox:

$V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)𝑑x$.

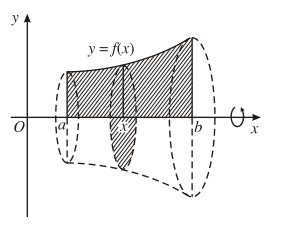
Ví dụ 3. Cho hình phẳng giới hạn bởi đường cong $y=x^2$, trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.

Lời giải:

Thể tích khối tròn xoay cần tính là:

$V=\pi \underset{0}{\overset{2}{\int }}{x}^4𝑑x={\pi \frac{x^5}{5}|}_0^2=\frac{32\pi }{5}.$