Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường (E): quay quanh Oy?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm thể tích V của vật tròn xoay sinh ra bởi đường tròn khi quay quanh trục Ox
Cho hàm số f(x) có đồ thị trên đoạn [−3;3] là đường gấp khúc ABCD như hình vẽ
Tính
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số , cung tròn có phương trình và trục hoành (phần tô đậm trong hình vẽ). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng D quanh trục Ox.
Cho hình phẳng (H) giới hạn bởi các đường và y = 0. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Oy là:
Một viên gạch hoa hình vuông cạnh 40cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường xung quanh trục Ox được tính theo công thức nào sau đây?
Một biển quảng cáo có dạng hình elip với bốn đỉnh như hình vẽ bên. Biết chi phí để sơn phần tô đậm là và phần còn lại là . Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết và tứ giác MNPQ là hình chữ nhật có MQ = 3m?
Tính thể tích hình xuyến do quay hình tròn có phương trình khi quanh trục Ox
Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích dùng để trồng hoa, phần diện tích dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là , kinh phí trồng cỏ là . Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
Cho hàm số có đồ thị (C) cắt trục hoành tại 4 điểm phân biệt. Gọi là diện tích hình phẳng giới hạn bởi trục hoành và phần đồ thị (C) nằm phía trên trục hoành, là diện tích hình phẳng giới hạn bởi trục hoành và phần đồ thị (C) nằm phía dưới trục hoành. Biết rằng . Giá trị của m là
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ Oxy là như hình vẽ bên. Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều dài 1 mét.
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị quay quanh trục Ox là với a, b > 0 và là phân số tối giản. Tính tổng T = a + b
Cho vật thể V được giới hạn bởi hai mặt phẳng x = 0 và x = - 2, mặt phẳng vuông góc với trục Ox cắt V theo thiết diện . Thể tích của V được tính bởi:
Viết công thức tính thể tích V của phần vật thể nằm giữa hai mặt phẳng x = 0 và x = ln4, biết khi cắt vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x , ta được thiết diện là một hình vuông có độ dài cạnh là:
Trong mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường và y = x. Thể tích của vật thể tròn xoay khi quay hình (H) quanh trục hoành một vòng bằng:
I. Tính diện tích hình phẳng
1. Hình phẳng giới hạn bởi một đường cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: .

Ví dụ 1. Tính diện tích hình phẳng được giới hạn bởi y = 5x4 + 3x2, trục hoành và hai đường thẳng x = 0; x = 1.
Lời giải:
Diện tích hình phẳng cần tính là:
2. Hình phẳng được giới hạn bởi 2 đường cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:
(*).
- Chú ý.
Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].
Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:
.
Ví dụ 2. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x2 – 1.
Lời giải:
Phương trình hoành độ giao điểm của hai đường cong:
x – 1 = x2 – 1
Diện tích hình phẳng đã cho là:
.
II. Tính thể tích
1. Thể tích của vật thể
Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm x cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].
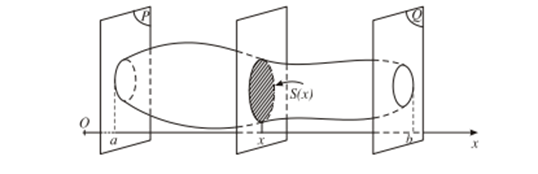
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức:
2. Thể tích khối chóp và khối chóp cụt.
a) Cho khối chóp có diện tích đáy là B, chiều cao h.
Khi đó, thể tích của khối chóp là
b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.
Thể tích của khối chóp cụt là:
III. Thể tích khối tròn xoay
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong y = f(x), trục hoành và hai đường thẳng x = a; x = b quanh trục Ox:
.
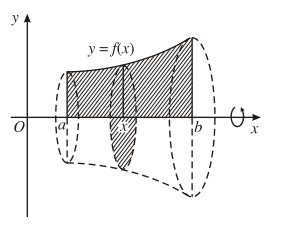
Ví dụ 3. Cho hình phẳng giới hạn bởi đường cong , trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.
Lời giải:
Thể tích khối tròn xoay cần tính là: