Tìm hệ số của trong khai triển :
A. 630
B. 635
C. 636
D.637
 Giải bởi Vietjack
Giải bởi Vietjack
Các biểu thức không chứa số hạng chứa .
Hệ số của số hạng chứa trong khai triển là
Hệ số của số hạng chứa trong khai triển là
Hệ số của số hạng chứa trong khai triển là
Hệ số của số hạng chứa trong khai triển là
Vậy hệ số của trong khai triển P(x) là .
Chọn đáp án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
I. Công thức nhị thức Niu- tơn
Ta có:
- Công thức nhị thức Niu – tơn.
- Hệ quả:
Với a = b = 1 ta có:
Với a = 1; b = – 1 ta có:
- Chú ý:
Trong biểu thức ở vế phải của công thức (1):
a) Số các hạng tử là n + 1.
b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước ).
c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.
- Ví dụ 1. Khai triển biểu thức: (a – b)^5.
Lời giải:
Áp dụng công thức nhị thức Niu – tơn ta có:
- Ví dụ 2. Khai triển biểu thức: (3x – 2)^4.
Lời giải:
Áp dụng công thức nhị thức Niu – tơn ta có:
II. Tam giác Pa- xcan
Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.
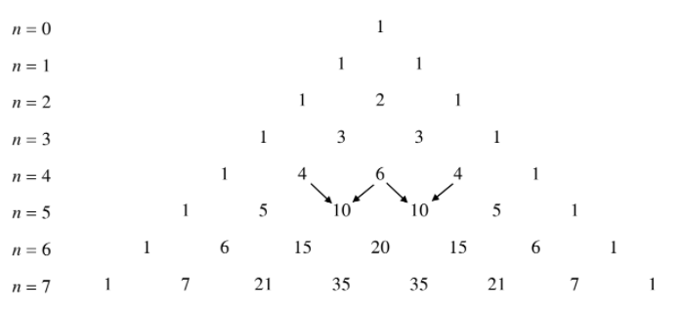
- Nhận xét:
Từ công thức suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.
Ví dụ 3. .