Cho hình chóp S.ABCDcó đáy là hình thoi, tam giác SABđều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD).Biết AC=2a, BD=4a.Tính theo akhoảng cách giữa hai đường thẳng ADvà SC
A. 4a√1391
B. a√16591
C. 4a√136591
D. a√13591
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
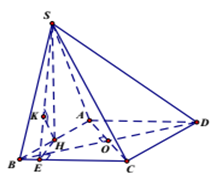
Gọi O=AC∩BD, H là trung điểm của AB suy ra SH⊥AB.
Do AB=(SAB)∩(ABCD) và (SAB)⊥(ABCD) nên SH⊥(ABCD)
Ta có: OA=AC2=2a2=a
OB=BD2=4a2=2a⇒Ab=√OA2+OB2=√a2+4a2=a√5
SH=AB√32=a√152;SABCD=12AC.BD=122a.4a=4a2
Thể tích khối chóp S.ABCD là
VS.ABCD=13SH.SABCD=13a√1524a2=2a3√153
Ta có: BC//AD⇒AD//(SBC)⇒d(AD,SC)=d(AD;(SBC))=d(A;(SBC))
Do H là trung điểm của AB và B=AH∩(SCB)⇒d(A;(SBC))=2d(H;(SBC))
Kẻ HE⊥BC,H∈BC. Do SH⊥BC⇒BC⊥(SHE).
Kẻ HK⊥SE,K∈SE, ta có BC⊥HK⇒HK⊥(SBC)⇒HK=d(H;(SBC))
HE=2SBCHBC=SABCBC=SABCD2BC=4a22a√5=2a√55
1HK2=1HE2+1SH2=54a2+415a2=9160a2⇒HK=2a√15√91=2a√136591
Vậy d(AD,SC)=2HK=4a√136591.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz , cho hai điểm A(2;1;2) và B(6;5;−4) . Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
Trong không gian Oxyz , hình chiếu vuông góc của điểm M(3;5;−2) trên mặt phẳng Oxy có tọa độ là
Cho hàm số có đồ thị như hình vẽ bên dưới.
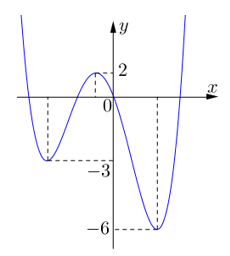
Gọi Slà tập tất cả các giá trị nguyên dương của tham số mđể hàm số y=|f(x−2018)+m−2|có đúng 5điểm cực trị. Số phần tử của Slà
Cho số phức z ; biết rằng các điểm biểu diễn hình học của số phức z ; iz và z+iz tạo thành một tam giác có diện tích bằng 18 . Mô đun của số phức z bằng
Trong không gian với hệ trục tọa độ Oxyz , cho điểm I(1; 0; −2) và mặt phẳng (P) có phương trình: x+2y−2z+4=0 . Phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P) là
Xét các số phức z=a+bi(a,b∈ℝ) thỏa mãn |z−4−3i|=√5. TínhP=a+b khi |z+1−3i|+|z−1+i| đạt giá trị lớn nhất.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB=3a,AD=2a ,SA vuông góc với mặt phẳng (ABCD) , SA=a . Gọi φ là góc giữa đường thẳng SCvà mp (ABCD) . Khi đó tanφ bằng bao nhiêu?
Cho mặt cầu(S):(x+1)2+(y−4)2+z2=8 và các điểm A(3;0;0) , B(4;2;1) . Gọi M là một điểm bất kỳ thuộc mặt cầu (S) . Tìm giá trị nhỏ nhất của biểu thức MA+2MB ?
