Với x ≥ 0 thì $\sqrt{x\sqrt{x\sqrt{x}}}$ bằng

I. Khái niệm lũy thừa

1. Lũy thừa với số mũ nguyên

Cho n là một số nguyên dương.

Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.

aⁿ = a.a.a… a (n thừa số a)

Với a ≠ 0, ta có: a⁰ = 1 và $a^{-n}=\frac{1}{a^n}$.

Trong biểu thức a^m ; ta gọi a là cơ số, số nguyên m là số mũ.

– Chú ý:

0⁰ và 0^–n không có nghĩa.

Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.

Ví dụ 1. Tính giá trị biểu thức:

$A={\left(\frac{1}{2}\right)}^{-3}\mathrm{.\hspace{0.17em}\hspace{0.17em}8}+{\mathrm{\hspace{0.17em}4}}^{-2}{\mathrm{.\hspace{0.17em}\hspace{0.17em}2}}^4+{\left(\frac{1}{3}\right)}^{-3}.\frac{1}{27}$

Lời giải:

$A={\left(\frac{1}{2}\right)}^{-3}\mathrm{.\hspace{0.17em}\hspace{0.17em}8}+{\mathrm{\hspace{0.17em}4}}^{-2}{\mathrm{.\hspace{0.17em}\hspace{0.17em}2}}^4+{\left(\frac{1}{3}\right)}^{-3}.\frac{1}{27}$

$\begin{array}{c}A={\mathrm{\hspace{0.17em}2}}^3\mathrm{.\hspace{0.17em}\hspace{0.17em}8}+{\left(\frac{1}{4}\right)}^2\mathrm{.\hspace{0.17em}16}+{\mathrm{\hspace{0.17em}3}}^3.\frac{1}{27}\\ A=\mathrm{\hspace{0.17em}8.8}+\frac{1}{16}.16+\mathrm{\hspace{0.17em}\hspace{0.17em}27}.\frac{1}{27}\end{array}$

A = 64 + 1 + 1 = 66.

2. Phương trình xⁿ = b.

Đồ thị của hàm số y = x^{2k + 1} có dạng tương tự đồ thị hàm số y = x³ và đồ thị hàm số y = x^2k có dạng tương tự đồ thị hàm số y = x⁴.

Từ đó, ta có kết quả biện luận số nghiệm của phương trình xⁿ = b như sau:

a) Trường hợp n lẻ:

Với mọi số thực b, phương trình có nghiệm duy nhất.

b) Trường hợp n chẵn:

Với b < 0, phương trình vô nghiệm.

Với b = 0 , phương trình có một nghiệm x = 0.

Với b > 0, phương trình có hai nghiệm đối nhau.

3. Căn bậc n

a) Khái niệm: Cho số thực b và số nguyên dương n $(n\ge 2)$. Số a được gọi là căn bậc n của số b nếu aⁿ  = b.

Ví dụ 2. Căn bậc ba của 27 là 3.

Căn bậc bốn của 256 là 4 và – 4.

– Từ định nghĩa và kết quả biện luận về số nghiệm của phương trình xⁿ = b; ta có:

Với n lẻ và $b\in R$: Có duy nhất một căn bậc n của b, kí hiệu là $\sqrt[n]{b}$.

Với n chẵn và :

+ b < 0 : không tồn tại căn bậc n của b.

+ b = 0: có một căn bậc n của b là số 0.

+ b > 0: có hai căn trái dấu; kí hiệu giá trị dương là $\sqrt[n]{b}$; còn giá trị âm là  $-\sqrt[n]{b}$.

b) Tính chất của căn bậc n

Từ định nghĩa ta có các tính chất sau:

$\begin{array}{c}\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}\\ \left\{\begin{array}{l}\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{\frac{a}{b}}\\ {\left(\sqrt[n]{a}\right)}^m=\sqrt[n]{a^m}\end{array}\right.\\ \end{array}$

$\sqrt[n]{a^n}=\{\begin{array}{c}a; khi n le\\ \left|a\right|; khi n chan\end{array}$

$\sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}$

Ví dụ 3. Rút gọn các biểu thức:

a) $\sqrt[3]{9}.\sqrt[3]{-3}$;

b)  $\sqrt[4]{{(-5)}^4}$ .

Lời giải:

a) $\sqrt[3]{9}.\sqrt[3]{-3}=\sqrt[3]{9.(-3)}=\sqrt[3]{-27}=-3$

b) $\sqrt[4]{{(-5)}^4}=|-5|=\mathrm{\hspace{0.17em}\hspace{0.17em}5}$.

4. Lũy thừa với số mũ hữu tỉ.

– Cho số thực a dương và số hữu tỉ $r=\frac{m}{n}$; trong đó $m\in Z;n\in N;n\ge 2$. Lũy thừa của a với số mũ r là số a^r xác định bởi:

Ví dụ 4. $\begin{array}{c}{27}^{\frac{1}{3}}=\sqrt[3]{27}=\mathrm{\hspace{0.17em}\hspace{0.17em}3}.\{9^{\frac{3}{2}}=\sqrt{9^3}=\mathrm{\hspace{0.17em}\hspace{0.17em}27}\end{array}$

5. Lũy thừa với số mũ vô tỉ.

Cho a là một số dương, α là một số vô tỉ. Ta thừa nhận rằng, luôn có một dãy số hữu tỉ (r_n) có giới hạn là α và dãy số tương ứng $\left(a^{r_n}\right)$ có giới hạn không phụ thuộc vào việc chọn dãy số (r_n).

– Ta gọi giới hạn của dãy số $\left(a^{r_n}\right)$ là thừa số của a với số  mũ α, kí hiệu là a^α.

– Chú ý: Từ định nghĩa, ta có: $1^{\alpha }=1;(\alpha \mathrm{ }\in R)$.

II. Tính chất lũy thừa với số mũ thực.

Cho a; b là những số thực dương, α, β là những số thực tùy ý. Khi đó, ta có:

$\begin{array}{c}{a}^{\alpha }.a^{\beta }=a^{\alpha \mathrm{ }+\beta }\\ a^{\alpha }{a}^{\beta }=a^{\alpha \mathrm{ }-\beta }\end{array}$

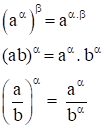
 Nếu a > 1 thì $a^{\alpha }>a^{\beta }$ khi và chỉ khi α > β.

Nếu a < 1 thì $a^{\alpha }>a^{\beta }$ khi và chỉ khi α < β.

Ví dụ 5. Rút gọn biểu thức:

Lời giải:

Với a > 0 ta có:

$A=\frac{a^{\sqrt{5}\mathrm{ }+\mathrm{\hspace{0.17em}2}}.a^{4-\sqrt{5}}}{{\left(a^{\sqrt{3}\mathrm{ }-1}\right)}^{\sqrt{3}\mathrm{ }+1}}=\frac{a^{\sqrt{5}\mathrm{ }+\mathrm{\hspace{0.17em}2}+\mathrm{\hspace{0.17em}\hspace{0.17em}4}-\sqrt{5}}}{a^{(\sqrt{3}\mathrm{ }-1).(\sqrt{3}\mathrm{ }+1)}}=\frac{a^6}{a^2}=a^4$.

Ví dụ 6. So sánh các số ${\left(\frac{2}{3}\right)}^{\sqrt{3}\mathrm{ }+\mathrm{\hspace{0.17em}1}}$ và ${\left(\frac{2}{3}\right)}^2$.

Lời giải:

Ta có: $\sqrt{3}+\mathrm{\hspace{0.17em}1}>\mathrm{\hspace{0.17em}2}$ và $0<\frac{2}{3}<\mathrm{\hspace{0.17em}\hspace{0.17em}1}$

Suy ra: ${\left(\frac{2}{3}\right)}^{\sqrt{3}+\mathrm{\hspace{0.17em}1}}$ <  ${\left(\frac{2}{3}\right)}^2$.