Có bao nhiêu số nguyên $a\in \left(-2019;2019\right)$ để phương trình $\frac{1}{\ln \left(x+5\right)}+\frac{1}{3^x-1}=x+a$ có hai nghiệm phân biệt?

I. Phương trình mũ

1. Phương  trình mũ cơ bản

– Phương trình mũ cơ bản có dạng: a^x = b (a > 0; a ≠ 1).

Để giải phương trình trên, ta sử dụng định nghĩa logarit.

Với b > 0 ta có: a^x = b $\iff$x = log_ab.

Với b ≤ 0, phương trình vô nghiệm.

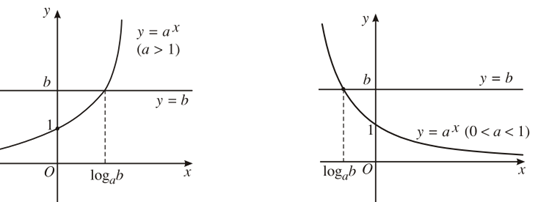
– Minh họa bằng đồ thị

Hoành độ giao điểm của đồ thị hai hàm số y = a^x và y = b là nghiệm của phương trình a^x = b.

Số nghiệm của phương trình là số giao điểm của hai đồ thị.

Rõ ràng, nếu b ≤ 0 thì hai đồ thị không cắt nhau nên phương trình vô nghiệm.

Nếu b > 0 ta có hai đồ thị như hình dưới đây. Trên mỗi hình, hai đồ thị luôn cắt nhau tại một điểm nên phương trình có nghiệm duy nhất.

Kết luận:

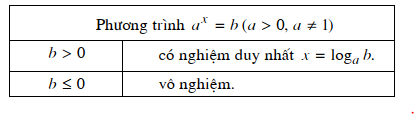
– Ví dụ 1. Giải phương trình 2^{x + 1} + 2^{x + 2} = 16.

Lời giải:

Ta có: 2^{x + 1} + 2^{x + 2} = 16.

$\iff$2.2^x + 4.2^x = 16

$\iff 2^x=\frac{8}{3}\iff x={\log }_2\frac{8}{3}$

Vậy $x={\log }_2\frac{8}{3}$.

2. Cách giải một số phương trình mũ cơ bản

a) Đưa về cùng cơ số.

– Ví dụ 2. Giải phương trình $3^{x+\mathrm{\hspace{0.17em}2}}={\left(\frac{1}{3}\right)}^{6-2x}$

Lời giải:

Ta có: $3^{x+\mathrm{\hspace{0.17em}2}}={\left(\frac{1}{3}\right)}^{6-2x}$

$\iff$ x + 2 = 2x – 6

Vậy x = 8.

b) Đặt ẩn phụ

– Ví dụ 3. Giải phương trình 4^x – 5. 2^x  + 6 = 0

Lời giải:

Đặt t = 2^x (với t > 0)

Phương trình đã cho trở thành: t² – 5t + 6 = 0

$\iff [\begin{array}{c}t=2\\ t=3\end{array}\Rightarrow [\begin{array}{c}{2}^x=\mathrm{\hspace{0.17em}\hspace{0.17em}2}\Rightarrow x=\mathrm{\hspace{0.17em}\hspace{0.17em}1}\\ 2^x=\mathrm{\hspace{0.17em}\hspace{0.17em}3}\Rightarrow x={\log }_{2}3\end{array}$

Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = log₂3.

c) Logarit hóa.

– Ví dụ 4. Giải phương trình: $3^x{\mathrm{.\hspace{0.17em}\hspace{0.17em}5}}^{x^2}=1$

Lời giải:

Lấy logarit cơ số 3 hai vế ta được:

$\begin{array}{c}{\log }_3\left(3^x{\mathrm{.\hspace{0.17em}\hspace{0.17em}5}}^{x^2}\right)={\log }_{3}1\Rightarrow x+x^2{\log }_{3}5=0\iff x(1+x{\log }_{3}5)=0\iff [\begin{array}{c}x=0\\ x=\frac{-1}{{\log }_{3}5}=-{\log }_{5}3\end{array}\end{array}$

Vậy phương trình đã cho có 2 nghiệm là x = 0 và x = – log₅3.

II. Phương trình logarit

– Phương trình logarit là phương trình có chứa ẩn số trong biểu thức dưới dấu logarit.

– Ví dụ 5. Các phương trình $\log {}_{2}x=\mathrm{\hspace{0.17em}4};{\log }_3^{2}x+\mathrm{\hspace{0.17em}2}{\log }_{4}x=0$… đều là phương trình logarit.

1. Phương trình logarit cơ bản

– Phương trình logarit cơ bản có dạng: log_ax = b (a > 0; a ≠ 1).

Theo định nghĩa logarit ta có:

log_ax = b $\iff$ x  = a^b

– Minh họa bằng đồ thị

Vẽ đồ thị hàm số y = log_a x và đường thẳng b trên cùng một hệ tọa độ.

Trong cả hai trường hợp, ta đều thấy đồ thị của các hàm số y = log_ax và đường thẳng y = b luôn cắt nhau tại một điểm với mọi b$\in R$.

Kết luận: Phương trình log_ax  = b (a > 0; a ≠ 1) luôn có nghiệm duy nhất x = a^b với mọi b.

2. Cách giải một số phương trình logarit đơn giản.

a) Đưa về cùng cơ số

Ví dụ 6. Giải phương trình log₃x + log₉x = 6.

Lời giải:

Ta có: log₃x + log₉x = 6

$\begin{array}{c}\iff {\log }_{3}x+\frac{1}{2}{\log }_{3}x=\mathrm{\hspace{0.17em}\hspace{0.17em}6}\iff \frac{3}{2}{\log }_{3}x=\mathrm{\hspace{0.17em}\hspace{0.17em}6}\iff {\log }_{3}x=4\end{array}$

Vậy nghiệm của phương trình đã cho là x = 81.

b) Đặt ẩn phụ

– Ví dụ 7. Giải phương trình ${\log }_5^{2}x+3{\log }_{5}x=0$

Lời giải:

Đặt t =log₅x, phương trình đã cho trở thành:

t² + 3t = 0 nên t = 0 hoặc t = –3.

Với t = 0 thì log₅x = 0 nên x = 1.

Với t = –3 thì log₅x = –3 nên x = 5^–3.

Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = 5^–3.

c) Mũ hóa

– Ví dụ 8. Giải phương trình: log₃(90 – 3^x) = x + 2

Lời giải:

Điều kiện của phương trình là 90 – 3^x > 0.

Phương trình đã cho tương đương với:

90 – 3^x = 3^{x + 2} hay 90 – 3^x = 9.3^x

Vậy nghiệm của phương trình đã cho là x = 2.