Cho hai số thực dương x,y thỏa mãn \[{2^x} + {2^y} = 4\]. Tìm giá trị lớn nhất PmaxPmax của biểu thức\[P = (2{x^2} + y)(2{y^2} + x) + 9xy\].
A.18
B.12
C.27
D.\[\frac{{27}}{2}\]
Giải bởi Vietjack
Ta có:
\[\begin{array}{l}4 = {2^x} + {2^y} \ge 2\sqrt {{2^x}{{.2}^y}} \\ \Rightarrow 2 \ge \sqrt {{2^x}{2^y}} \\ \Rightarrow 4 \ge {2^{x + y}}\\ \Rightarrow 0 < x + y \le 2\\ \Rightarrow {(x + y)^2} \le 4\end{array}\]
Lại có\[x + y \ge 2\sqrt {xy} \Rightarrow xy \le 1\]
\[\begin{array}{*{20}{l}}{ \Rightarrow P = 4{x^2}{y^2} + 2{x^3} + 2{y^3} + 10xy}\\{ = 4{{\left( {xy} \right)}^2} + 10xy + 2\left( {{x^3} + {y^3}} \right)}\\{ = 4{{\left( {xy} \right)}^2} + 10xy}\\{ + 2.\left( {x + y} \right).\left[ {{{\left( {x + y} \right)}^2} - 3xy} \right]}\\{ \Rightarrow P \le 4{{\left( {xy} \right)}^2} + 10xy + 2.2.\left( {4 - 3xy} \right)}\\{ \Rightarrow P \le 4{{\left( {xy} \right)}^2} - 2xy + 16}\end{array}\]
Đặt \[xy = t \Rightarrow 0 < t \le 1\]
Xét hàm số \[f\left( t \right) = 4{t^2} - 2t + 16\] trên\[\left( {0;1} \right]\]
\[ \Rightarrow f\left( t \right) \le \max \left\{ {f\left( 1 \right),f\left( 0 \right)} \right\} = 18\]
Dấu “=” xảy ra khi và chỉ khi x = y = 1.
Vậy\[{P_{\max }} = 18 \Leftrightarrow x = y = 1\]
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho giới hạn \[I = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{3x}} - {e^{2x}}}}{x}\], chọn mệnh đề đúng:
Hàm số nào sau đây nghịch biến trên \[\left( { - \infty ; + \infty } \right)\]?
Cho các đồ thị hàm số \[y = {a^x},y = {b^x},y = {c^x}(0 < a,b,c \ne 1)\] chọn khẳng định đúng:
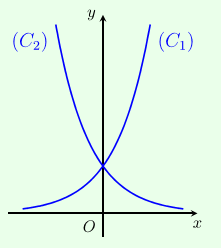
Cho hai hàm số \[y = {a^x},y = {b^x}\] với \[1 \ne a,b > 0\;\]lần lượt có đồ thị là (C1),(C2) như hình bên. Mệnh đề nào đúng?
