Cho hình nón \[\left( N \right)\] có đường cao bằng \[a\sqrt 3 \], đáy của \[\left( N \right)\] có bán kính bằng a. Thiết diện qua đỉnh của \[\left( N \right)\] là một tam giác có chu vi bằng 5a. Tính theo a diện tích S của tam giác này.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
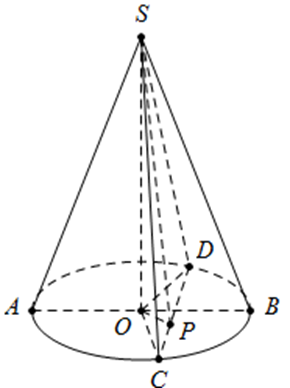
Thiết diện qua đỉnh của \[\left( N \right)\] là \[\Delta SCD\] như hình vẽ.
\[\begin{array}{l}S{C^2} = S{O^2} + O{C^2} = 3{a^2} + {a^2} \Rightarrow SC = 2a.\\S{D^2} = S{O^2} + O{D^2} = 3{a^2} + {a^2} \Rightarrow SD = 2a.\end{array}\]
Bài ra có chu vi \[\Delta SCD\] bằng 5a
\[ \Rightarrow SC + SD + CD = 5a \Rightarrow 4a + CD = 5a \Rightarrow CD = a\].
Kẻ \[SP \bot CD\] mà \[SC = SD = 2a\].
\[\begin{array}{l} \Rightarrow PC = PD = \frac{{CD}}{2} = \frac{a}{2} \Rightarrow S{P^2} = S{C^2} - C{P^2} = 4{a^2} - \frac{{{a^2}}}{4}\\ \Rightarrow SP = \frac{{a\sqrt {15} }}{2} \Rightarrow {S_{SCD}} = \frac{1}{2}CD.SP = \frac{1}{2}a.\frac{{a\sqrt {15} }}{2} = \frac{{{a^2}\sqrt {15} }}{4}.\end{array}\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \[y = \frac{1}{3}m{x^3} - m{x^2} + 3x + 1\]. Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\]?
Cho hai số phức \[{z_1} = 3 + 2i,{z_2} = 1 - i\]. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức \[\frac{{{z_1}}}{{{z_2}}}\] có tọa độ là:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm của cạnh AB. Thể tích khối chóp S.ABC bằng \[\frac{{{a^3}\sqrt 3 }}{3}\]. Khoảng cách từ điểm A đến mặt phẳng \[\left( {SBC} \right)\] bằng:
Trong không gian Oxyz, hình chiếu vuông góc của điểm \[M\left( {1;2; - 3} \right)\] trên trục Oz có tọa độ là
Giá trị lớn nhất của hàm số \[y = {x^4} - 2{x^2} + 5\] trên đoạn \[\left[ {0;2} \right]\] bằng:
Tìm nguyên hàm của hàm số \[f\left( x \right) = {e^x}\sqrt {{e^x} + 1} \].
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \[y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\] trên đoạn \[\left[ {1;2} \right]\] bằng 2. Số phần tử của S là:
Cho hàm số \[y = f\left( x \right)\] có bảng xét dấu của \[f'\left( x \right)\] như sau:
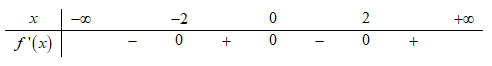
Bất phương trình \[f\left( x \right) < {e^{{x^2}}} + m\] đúng với mọi \[x \in \left( { - 1;0} \right)\] khi và chỉ khi
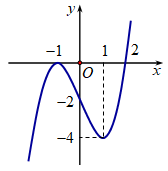
Cho hàm số bậc bốn \[y = f\left( x \right)\] thỏa mãn \[f\left( 0 \right) = 7\]. Hàm số \[y = f'\left( x \right)\] có đồ thị như hình vẽ. Hàm số \[y = {\left( {f\left( x \right)} \right)^2}\] đồng biến trên khoảng nào dưới đây?
Trong không gian Oxyz, cho đường thẳng . Đường thẳng d đi qua điểm có tọa độ nào dưới đây?
Có bao nhiêu số nguyên m lớn hơn \[ - 10\] để hàm số \[f\left( x \right) = \frac{{{x^3}}}{3} + m{x^2} + 3x + 5m - 1\] nghịch biến trên khoảng \[\left( {1;3} \right)\]?
Cho khối chóp tứ giác S.ABCD. Mặt phẳng đi qua trọng tâm các tam giác SAB, SAC, SAD chia khối chóp này thành hai phần có thể tích là \[{V_1}\] và \[{V_2}\left( {{V_1} < {V_2}} \right)\]. Tính tỉ số \[\frac{{{V_1}}}{{{V_2}}}\].
Trong không gian Oxyz, cho hai điểm \[A\left( {1;3;10} \right),B\left( {4;6;5} \right)\] và M là điểm thay đổi trên mặt phẳng \[\left( {Oxy} \right)\] sao cho MA, MB cùng tạo với \[\left( {Oxy} \right)\] hai góc bằng nhau. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng AM.