Một lớp có 19 học sinh nữ và 25 học sinh nam. Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác tham gia một hoạt động của Đoàn trường. Xác suất để 4 học sinh được chọn có cả nam và nữ bằng (làm tròn đến chữ số thập phân thứ 4).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Theo bài ra, bạn lớp trưởng sẽ chọn ngẫu nhiên 4 học sinh trong 19 học sinh nữ và 25 học sinh nam.
Số cách chọn 4 học sinh trong 44 học sinh của lớp là: \[C_{44}^4 = 135751\].
Số cách chọn cả 4 học sinh đều là nữ là: \[C_{19}^4\].
Số cách chọn cả 4 học sinh đều là nam là: \[C_{25}^4\].
Số cách chọn 4 học sinh trong đó có cả nam và nữ là: \[C_{44}^4 - C_{19}^4 - C_{25}^4 = 119225\] cách.
Xác suất để 4 học sinh được chọn có cả nam và nữ là: \[\frac{{119225}}{{135751}} \approx 0,8783\].
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ Oxyz cho đường thẳng \[{d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\\z = 3\end{array} \right.\] và \[{d_2}:\left\{ \begin{array}{l}x = 1\\y = 2 + 7t'\\z = 3 + t'\end{array} \right.\]. Phương trình đường phân giác của góc tù giữa \[{d_1}\] và \[{d_2}\] là:
Hệ số của số hạng chứa \[{x^7}\] trong khai triển nhị thức \[{\left( {x - \frac{2}{{x\sqrt x }}} \right)^{12}}\] (với \[x > 0\]) là:
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
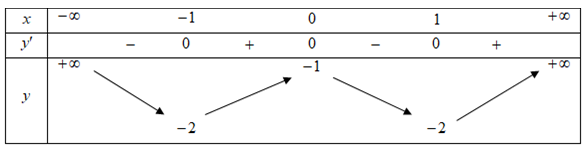
Số điểm cực tiểu của hàm số \[g\left( x \right) = 2{f^3}\left( x \right) + 4{f^2}\left( x \right) + 1\] là:
Trong không gian Oxyz, có tất cả bao nhiêu giá trị nguyên của m để \[{x^2} + {y^2} + {z^2} + 2\left( {m + 2} \right)x - 2\left( {m - 1} \right)z + 3{m^2} - 5 = 0\] là phương trình của một mặt cầu?
Trong không gian Oxyz, cho \[\overrightarrow {OA} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \], điểm \[B\left( {3; - 4;1} \right)\] và điểm \[C\left( {2;0; - 1} \right)\]. Tọa độ trọng tâm của tam giác ABC là:
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đạo hàm \[f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\] với mọi \[x \in \mathbb{R}\]. Có bao nhiêu số nguyên m thuộc đoạn \[\left[ { - 2019;2019} \right]\] để hàm số \[g\left( x \right) = f\left( {1 - x} \right)\] nghịch biến trên khoảng \[\left( { - \infty ; - 1} \right)\]?
Cho tập A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử?
Kí hiệu \[{z_1}\] và \[{z_2}\] là hai nghiệm phức của phương trình \[{z^2} + z + 1 = 0\]. Tính \[P = z_1^2 + z_2^2 + {z_1}{z_2}\].
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \[\widehat {ABC} = 60^\circ \]. Hình chiếu vuông góc của điểm S lên mặt phẳng \[\left( {ABCD} \right)\] trùng với trọng tâm tam giác ABC. Gọi \[\varphi \] là góc giữa đường thẳng SB với mặt phẳng \[\left( {SCD} \right)\], tính \[\sin \varphi \] biết rằng \[SB = a\].
Cho a là số thực dương khác 5. Tính \[I = {\log _{\frac{a}{5}}}\left( {\frac{{{a^3}}}{{125}}} \right)\].
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E, F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng \[\left( {AEF} \right)\] cắt khối lập phương đã cho thành hai phần, gọi \[{V_1}\] là thể tích khối chứa điểm A’ và \[{V_2}\] là thể tích khối chứa điểm C’. Khi đó \[\frac{{{V_1}}}{{{V_2}}}\] là:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[\left( P \right):2x - 4y + 6z - 1 = 0\]. Mặt phẳng \[\left( P \right)\] có một vectơ pháp tuyến là:
Cho hàm số \[y = f\left( x \right)\] liên tục và có đạo hàm trên \[\mathbb{R}\] thỏa mãn \[f\left( 2 \right) = - 2;\int\limits_0^2 {f\left( x \right)dx} = 1\]. Tính tích phân \[I = \int\limits_{ - 1}^3 {f'\left( {\sqrt {x + 1} } \right)dx} \].
Cho z và w là các số phức thỏa mãn các điều kiện \[z\left( {w + 1} \right) + iw - 1 = 0,\left| {w + 2} \right| = 1\]. Giá trị nhỏ nhất của biểu thức \[T = \left| {z - 1 - 3i} \right|\] bằng:
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như hình vẽ sau:
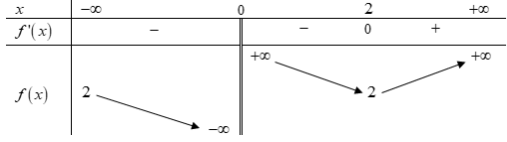
Hàm số nghịch biến trên khoảng nào sau đây?