Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\frac{{x - 4}}{2} = \frac{{y - 1}}{1} = \frac{{z - 2}}{1}.\] Xét mặt phẳng \[\left( P \right):x - 3y + 2mz - 4 = 0,\] với m là tham số thực. Tìm tất cả các giá trị thực của m để đường thẳng d song song với mặt phẳng (P).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Đường thẳng d qua \(A\left( {4;1;2} \right)\) có một VTCP là \(\overrightarrow u = \left( {2;1;1} \right).\)
Mặt phẳng \(\left( P \right)\) có một VTPT là \(\overrightarrow n = \left( {1; - 3;2m} \right).\)
YCBT\( \Leftrightarrow \left\{ \begin{array}{l}A \notin \left( P \right)\\\overrightarrow u .\overrightarrow n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 - 3.1 + 2m.2 - 4 \ne 0\\2 - 3 + 2m = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m - 3 \ne 0\\m = \frac{1}{2}\end{array} \right. \Leftrightarrow m = \frac{1}{2}.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một hộp đựng 9 thẻ được đánh số 1, 2, 3, 4, ……, 9. Rút ngẫu nhiên đồng thời 2 thẻ và nhân hai số ghi trên hai thẻ lại với nhau. Tính xác suất để tích nhận được là số chẵn.
Cho hai số phức \[{z_1},{z_2}\] thỏa mãn \[\left| {{z_1} - {z_2}} \right| = \left| {{z_1}} \right| = \left| {{z_2}} \right| > 0\]. Tính \[{\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^4} + {\left( {\frac{{{z_2}}}{{{z_1}}}} \right)^4}\].
Cho \[\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = 5.\] Tích phân \[\int\limits_0^{\frac{\pi }{2}} {\left[ {\cos x + f\left( x \right)} \right]dx} \] bằng
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x - 2y + z - 3 = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{{ - 1}}.\] Mặt phẳng \[\left( Q \right):ax + by + cz - 4 = 0\] chứa đường thẳng d và vuông góc với mặt phẳng (P). Tính \[a + b + c.\]
Trong không gian Oxyz, cho ba điểm \[A\left( {1;0;0} \right)\], \[B\left( {0;2;0} \right)\], \[C\left( {0;0;3} \right)\]. Tập hợp các điểm M thỏa mãn \[M{A^2} = M{B^2} + M{C^2}\] là mặt cầu có bán kính bằng
Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là 6cm, chiều dài lăn là 25cm (như hình vẽ). Sau khi lăn trọn 10 vòng thì trục lăn tạo nên bức tường phẳng có diện tích là

Trong không gian Oxyz, cho vectơ \[\vec a = 2\vec i + \vec k - 3\vec j.\] Tọa độ của vectơ \[\vec a\] là
Cho hàm số \[y = \frac{5}{6}{x^3} + mx - \frac{2}{3}m\] có đồ thị (C), với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m để từ điểm \[A\left( {\frac{2}{3};0} \right)\] kẻ đến (C) được hai tiếp tuyến vuông góc với nhau. Tính tổng tất cả các phần tử của \[S.\]
Cho hàm số f(x) liên tục trên khoảng \[\left( {0; + \infty } \right)\] thỏa mãn \[f\left( 1 \right) = 1\] và \[f'\left( x \right) \ge x + \frac{1}{x},{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {0; + \infty } \right)\]. Tìm giá trị nhỏ nhất của \[f\left( 2 \right)\].
Cho tứ diện ABCD có \[AB,{\rm{ }}AC,{\rm{ }}AD\] đôi một vuông góc với nhau và \[AB = 2a,{\rm{ }}AC = 3a,{\rm{ }}AD = 4a.\] Thể tích của khối tứ diện ABCD bằng
Cho a và b là hai số thực dương khác 1 và các hàm số \[y = {a^x},{\rm{ }}y = {b^x}\] có đồ thị như hình vẽ.
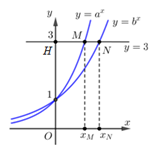
Đường thẳng \[y = 3\] cắt trục tung, đồ thị hàm số \[y = {a^x},{\rm{ }}y = {b^x}\] lần lượt tại các điểm \[H,{\rm{ }}M,{\rm{ }}N.\] Biết rằng \[HM = 2MN.\] Mệnh đề nào sau đây đúng?
Trong không gian, cho hình trụ (T). Mặt phẳng (α) song song với trục của (T), cắt (T) theo thiết diện (D) là một hình vuông có diện tích bằng \[64c{m^2}.\] Khoảng cách từ trục của (T) đến mặt phẳng chứa (D) bằng 3cm. Tính thể tích của khối trụ đã cho.
Cho cấp số nhân \[\left( {{u_n}} \right)\] với \[{u_1} = 3,{\rm{ }}{u_6} = \frac{3}{{32}}.\] Tìm q.
Cho hàm số f(x) có bảng biến thiên như sau:
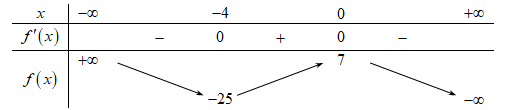
Phương trình \[f\left( x \right) - 7 = 0\] có số nghiệm thực là