Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thuộc [1; 2]?
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Đặt ẩn phụ đưa phương trình về dạng m = f(t) với
- Tìm đạo hàm và lập bảng biến thiên hàm số f(x) trên [a; b] và tìm các giá trị m thỏa mãn.
Cách giải:
Đặt ta có: Hàm số f(x) đồng biến trên [1; 2].
Do đó
Ta có
Khi đó phương trình đã cho có dạng
có nghiệm
có nghiệm .
có nghiệm
Xét
Bảng biến thiên:
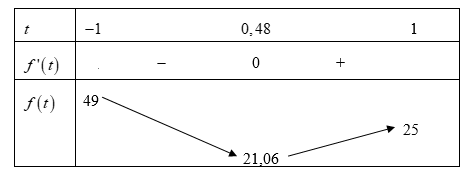
Từ bảng biến thiên ta suy ra
Vậy có 28 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hàm số y = f(x) liên tục trên [2; 9]. F(x) là một nguyên hàm của hàm số f(x) trên [2; 9] và Mệnh đề nào sau đây đúng?
Cho hàm số bậc ba y = f(x) có đồ thị của hàm số f'(x) như hình vẽ và f(b) = 1. Số giá trị nguyên của để hàm số có đúng 5 điểm cực trị là:
Cho tứ diện ABCD có cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6, AC = 7, AD = 4. Gọi M, N, P tương ứng là trung điểm các cạnh . Tính thể tích V của khối tứ diện ABCD.
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có bảng biến thiên như sau:
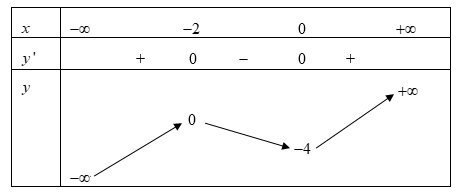
Số nghiệm của phương trình f(x) + 3 = 0 là:
Cho hàm số y = f(x) có đạo hàm . Số điểm cực tiểu của hàm số đã cho là
Cho hình hình hộp chữ nhật ABCD.A'B'C'D' có và AD = a. Góc giữa hai đường thẳng B'D' và AC bằng