Giải Sách bài tập Toán 10 Kết nối tri thức Bài 7: Các khái niệm mở đầu
Với giải sách bài tập Toán 10 Bài 7: Các khái niệm mở đầu sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 7.
Giải sách bài tập Toán lớp 10 Bài 7: Các khái niệm mở đầu
Bài 4.1 trang 47 SBT Toán 10 Tập 1: Cho tam giác ABC. Gọi M là trung điểm của cạnh BC và G là trọng tâm của tam giác. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
a) Hai vectơ và cùng phương;
b) Hai vectơ và cùng hướng;
c) Hai vectơ và ngược hướng;
d) Độ dài của vectơ bằng ba lần độ dài của vectơ .
Lời giải:
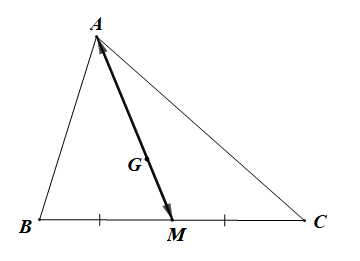
Ta có: M là trung điểm của BC và G là trọng tâm của tam giác ABC
Nên trung tuyến AM đi qua điểm G.
+ Hai vectơ và cùng phương vì chúng có giá trùng nhau.
Do đó khẳng định a) là đúng.
+ Hai vectơ và ngược hướng
Do đó khẳng định b) là sai và khẳng định c) là đúng.
+ Vì G là trọng tâm tam giác ABC nên
AM = 3MG.
Do đó
Do đó khẳng định d) là đúng.
Vậy các khẳng định đúng là: a), c) và d).
Bài 4.2 trang 47 SBT Toán 10 Tập 1: Cho trước hai vectơ không cùng phương và . Hỏi có hay không một vectơ cùng phương với cả và
Lời giải:
Vì vectơ cùng phương với mọi vectơ nên:
+ Vectơ cùng phương với
+ Vectơ cùng phương với
Do đó có một vectơ cùng phương với cả và .
Bài 4.3 trang 47 SBT Toán 10 Tập 1: Cho ba vectơ cùng phương và cùng khác vectơ . Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng.
Lời giải:
Ba vectơ cùng phương và cùng khác vectơ nên chúng có thể cùng hướng hoặc ngược hướng nhau.
Trường hợp 1: Nếu cùng hướng với (hoặc cùng hướng với )
Thì khi đó có hai vectơ cùng hướng.
Trường hợp 2: Nếu ngược hướng với cả và
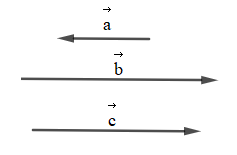
Vì ngược hướng với , ngược hướng với
Nên khi đó và cùng hướng với nhau.
Do đó có hai vectơ trong ba vectơ cùng hướng với nhau
Vậy có ít nhất hai vectơ trong ba vectơ có cùng hướng.
Bài 4.4 trang 47 SBT Toán 10 Tập 1: Cho lục giác đều ABCDEF có tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F.
a) Hãy chỉ ra các vectơ khác vectơ - không và cùng phương với vectơ
b) Tìm các vectơ bằng vectơ .
Lời giải:
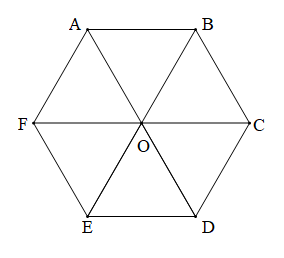
Do ABCDEF là lục giác đều tâm O nên:
+ Các cặp cạnh đối diện bằng nhau: AB = ED, BC = FE, CD = FA;
+ Ba đường chéo chính AD, BE, CF đồng quy tại trung điểm của mỗi đường;
+ Mỗi đường chéo chính song song với một cặp cạnh có đầu mút không thuộc đường chéo ấy.
a) Các vectơ khác vectơ - không và cùng phương với vectơ mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là:
b) Vectơ bằng vectơ mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là:
Bài 4.5 trang 47 SBT Toán 10 Tập 1:
Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn (O).
a) Chứng minh rằng
b) Gọi M là trung điểm cạnh BC. Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ và
Lời giải:
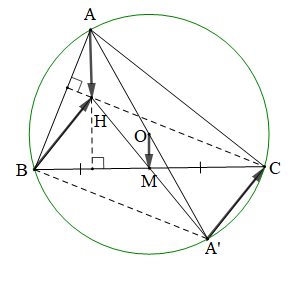
a) Vì H là trực tâm tam giác ABC nên CH ⊥ AB
Mặt khác AA' là đường kính của (O), B ∈ (O) nên
Do đó AA' ⊥ AB
Suy ra CH // AA' (từ vuông góc đến song song)
Chứng minh tương tự ta cũng có BH // A'C
Tứ giác BHCA' có CH // AA' và BH // A'C
Suy ra BHCA' là hình bình hành
Do đó
b) Ta có: O và M lần lượt là trung điểm của AA' và BC
Nên OM là đường trung bình của tam giác AA'H
Do đó AH = 2OM và OM // AH (tính chất đường trung bình)
Vậy, hai vectơ và có:
+ Cùng phương
+ Cùng hướng
+
Bài 4.6 trang 48 SBT Toán 10 Tập 1: Trên biển Đông, một tàu chuyển động đều từ vị trí A theo hướng N20°E với vận tốc 20 km/h. Sau 2 giờ, tàu đến được vị trí B. Hỏi A cách B bao nhiêu kilômét và hướng nào so với B?
Lời giải:
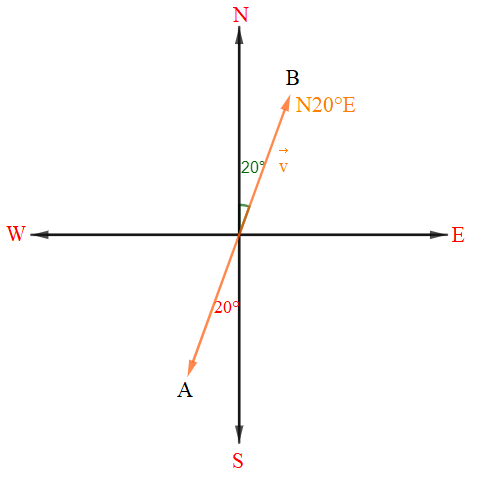
Ta sử dụng vectơ với (km/h) để biểu thị vận tốc của tàu, vectơ biểu thị cho quãng đường và hướng chuyển động của tàu từ A tới B (hình vẽ trên).
Vì tàu chuyển động đều từ A với vận tốc 20 km/h trong 2 giờ tới B nên (km).
Vậy A cách B 40 km.
Do tàu chuyển động đều từ vị trí A theo hướng N20°E đến vị trí B
Do đó A ở hướng ngược lại so với B, tức là hướng S20°W so với B.
Bài viết liên quan
- Giải Sách bài tập Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vectơ
- Giải Sách bài tập Toán 10 Kết nối tri thức Bài 13: Các số đặc trưng đo xu thế trung tâm
- Giải Sách bài tập Toán 10 Kết nối tri thức Bài 14: Các số đặc trưng đo độ phân tán
- Giải Sách bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 5
- Giải Sách bài tập Toán 10 Kết nối tri thức Bài 12: Số gần đúng và sai số
