Cho tam giác ABC (\(\widehat B = 90^\circ \)) có đường cao BD. Gọi E, F lần lượt là trung điểm của BD, DC và H là giao điểm của AE, BF. Tính \(\widehat {AHB}\)?
 Giải bởi Vietjack
Giải bởi Vietjack
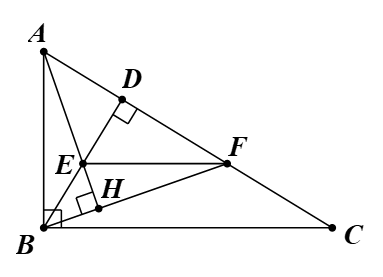
Tam giác BCD có E, F lần lượt là trung điểm của BD, DC.
Suy ra EF là đường trung bình của tam giác BCD.
Do đó EF // BC.
Mà BC ⊥ AB (\(\widehat {ABC} = 90^\circ \)).
Vì vậy EF ⊥ AB.
Tam giác ABF có hai đường cao BD, EF cắt nhau tại E.
Suy ra E là trực tâm của tam giác ABF.
Do đó AE ⊥ BF hay AH ⊥ BF.
Vậy \(\widehat {AHB} = 90^\circ \).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có tất cả 40 con vừa gà vừa chó. Số chân chó nhiều hơn số chân gà là 16 chân. Hỏi có bao nhiêu gà, bao nhiêu chó?
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, \(BC = a\sqrt 3 \). Tam giác SOA cân tại S và nằm trong mặt phẳng vuông góc với đáy. SC tạo với mặt phẳng đáy một góc 60°. Tính thể tích khối chóp S.ABCD.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Cho ba số dương x, y, z thỏa mãn x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{1}{{x + y}} + \frac{1}{{y + z}} + \frac{1}{{z + x}}\).
Cho phương trình (1 + m)x2 – 2mx + 2m = 0. Tìm m để phương trình:
a) Có nghiệm.
b) Vô nghiệm.
c) Có 2 nghiệm.
d) Có 2 nghiệm phân biệt.
Cho tam giác ABC vuông cân tại A. Trên các cạnh góc vuông AB, AC lấy D và E sao cho AD = AE. Qua D vẽ đường thẳng vuông góc với BE cắt BC ở K. Qua A vẽ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh rằng:
a) ∆BAE = ∆CAD;
b) ∆MDC cân;
c) HK = HC.
Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn biết rằng ba bạn có 44 viên bi.
Cho tam giác ABC có \(\widehat A = 60^\circ \). Các tia phân giác của \(\widehat B\) và \(\widehat C\) cắt nhau ở I, cắt cạnh AC, AB ở D và E. Tia phân giác của \(\widehat {BIC}\) cắt BC ở F.
a) Tính \(\widehat {BIC}\).
b) Chứng minh ID = IE = IF.
c) Chứng minh tam giác DEF đều.
d) Chứng minh I là giao điểm các đường phân giác của hai tam giác ABC và DEF.
Cho tam giác ABC có các góc thỏa mãn \(\frac{{\sin A}}{1} = \frac{{\sin B}}{2} = \frac{{\sin C}}{{\sqrt 3 }}\). Tính số đo các góc của tam giác.
Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng:
\(\frac{1}{{{a^3}\left( {b + c} \right)}} + \frac{1}{{{b^3}\left( {c + a} \right)}} + \frac{1}{{{c^3}\left( {a + b} \right)}} \ge \frac{3}{2}\).
Cho tập hợp A = {1; 2; 3; 4; 5; 6; 7; 8}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên có 6 chữ số khác nhau và phải có mặt các chữ số 1, 2, 3 sao cho chúng không đứng cạnh nhau?
Tam giác ABC có \(\widehat A = 60^\circ \), các cạnh b = 20 c = 35.
a) Tính chiều cao ha.
b) Tính bán kính đường tròn ngoại tiếp tam giác.
c) Tính bán kính đường tròn nội tiếp tam giác.
Cho \(\left( {x + \sqrt {2005 + {x^2}} } \right)\left( {y + \sqrt {2005 + {y^2}} } \right) = 2005\). Tính x2005 + y2005.