B. \(\frac{{11}}{3}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Đáp án đúng là: A
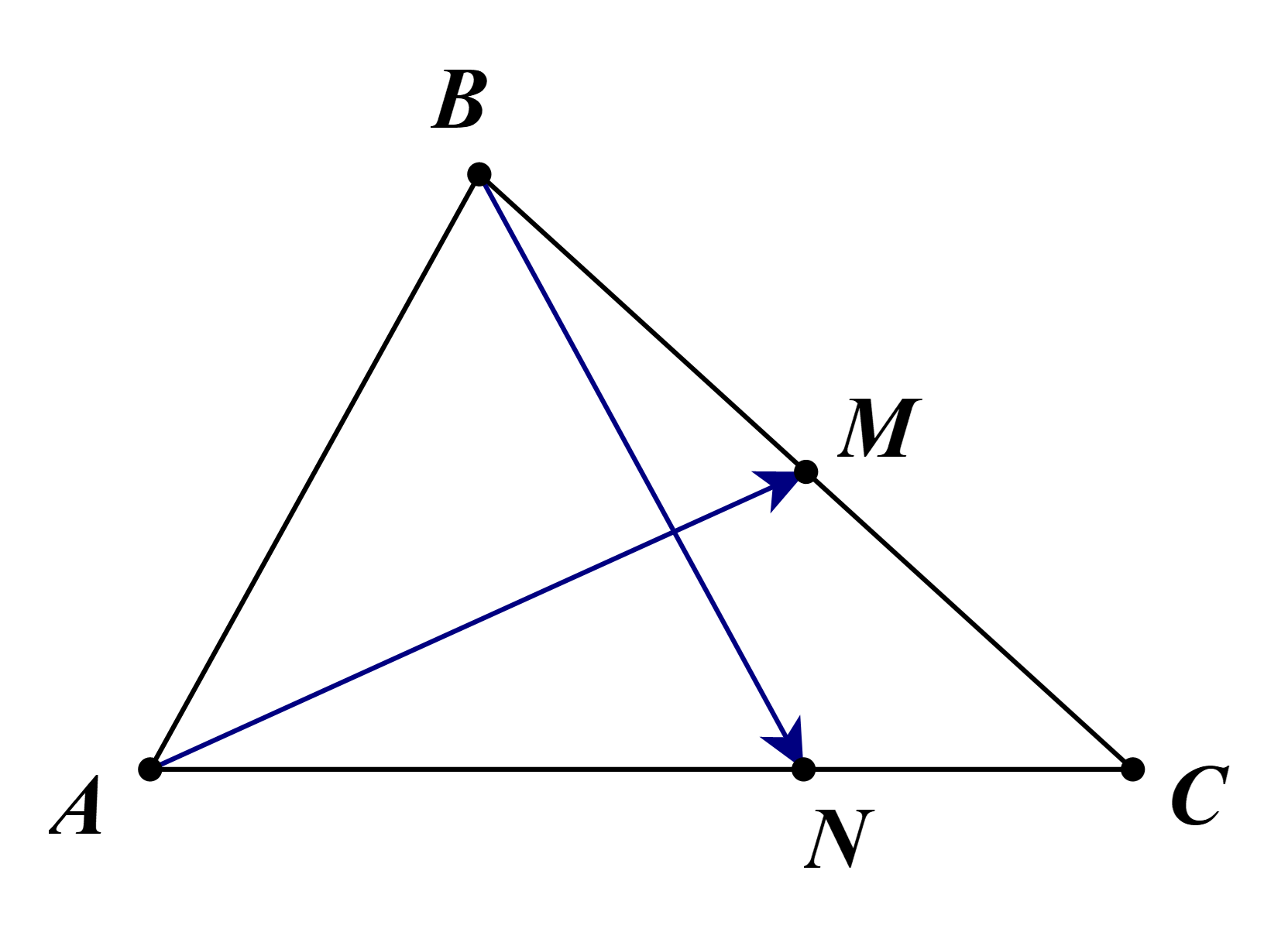
Ta có AC = 3NC. Suy ra \(AN = \frac{2}{3}AC = 6\) và \[\overrightarrow {AN} = \frac{2}{3}\overrightarrow {AC} \].
Tam giác ABC có AM là đường trung tuyến.
Suy ra \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
Ta có \(\overrightarrow {AM} .\overrightarrow {BN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AN} - \overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AN} - A{B^2} + \overrightarrow {AC} .\overrightarrow {AN} - \overrightarrow {AC} .\overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {AB.AN.\cos \widehat {BAC} - A{B^2} + \frac{2}{3}A{C^2} - AC.AB.\cos \widehat {BAC}} \right)\)
\( = \frac{1}{2}\left( {AN.\frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AC}} - A{B^2} + \frac{2}{3}A{C^2} - \frac{{A{B^2} + A{C^2} - B{C^2}}}{2}} \right)\)
\( = \frac{{26}}{3}\).
Vậy ta chọn phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
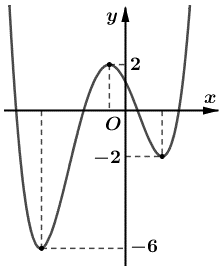
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.
a) Chứng minh AD = BC.
b) Gọi E là giao điểm của AD và BC. Chứng minh ∆EAC = ∆EBD.
c) Chứng minh OE là phân giác của \(\widehat {xOy}\).
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
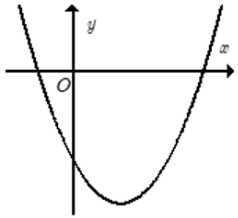
Khẳng định nào sau đây đúng?
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC.
a) Chứng minh rằng BE = CD.
b) Chứng minh BE // CD.
c) Gọi M là trung điểm của BE và N là trung điểm của CD. Chứng minh AM = AN.
Tính tổng sau đây:
\(C_{2021}^0 - 2.C_{2021}^1 + {2^2}.C_{2021}^2 - {2^3}.C_{2021}^3 + ... - {2^{2021}}.C_{2021}^{2021}\).
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ bên.
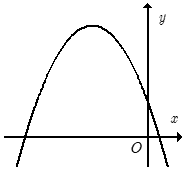
Khẳng định nào sau đây đúng?