Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 33)
-
2155 lượt thi
-
52 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Xét phương trình f(x) = 0 ⇔ mx + m – 1 = 0.
Trường hợp 1: m = 0.
Khi đó phương trình f(x) = 0 ⇔ 0.x = 1 (vô nghiệm).
Vì vậy ta loại m = 0.
Trường hợp 2: m ≠ 0.
Phương trình \(f\left( x \right) = 0 \Leftrightarrow x = \frac{{1 - m}}{m}\).
Phương trình f(x) = 0 có nghiệm thuộc (3; 4).
\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 - m}}{m} > 3\\\frac{{1 - m}}{m} < 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 - 4m}}{m} > 0\\\frac{{1 - 5m}}{m} < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}0 < m < \frac{1}{4}\\\left[ \begin{array}{l}m < 0\\m > \frac{1}{5}\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \frac{1}{5} < m < \frac{1}{4}\).
So với điều kiện m ≠ 0, ta nhận \(\frac{1}{5} < m < \frac{1}{4}\).
Vậy \(\frac{1}{5} < m < \frac{1}{4}\) thỏa mãn yêu cầu bài toán.
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải
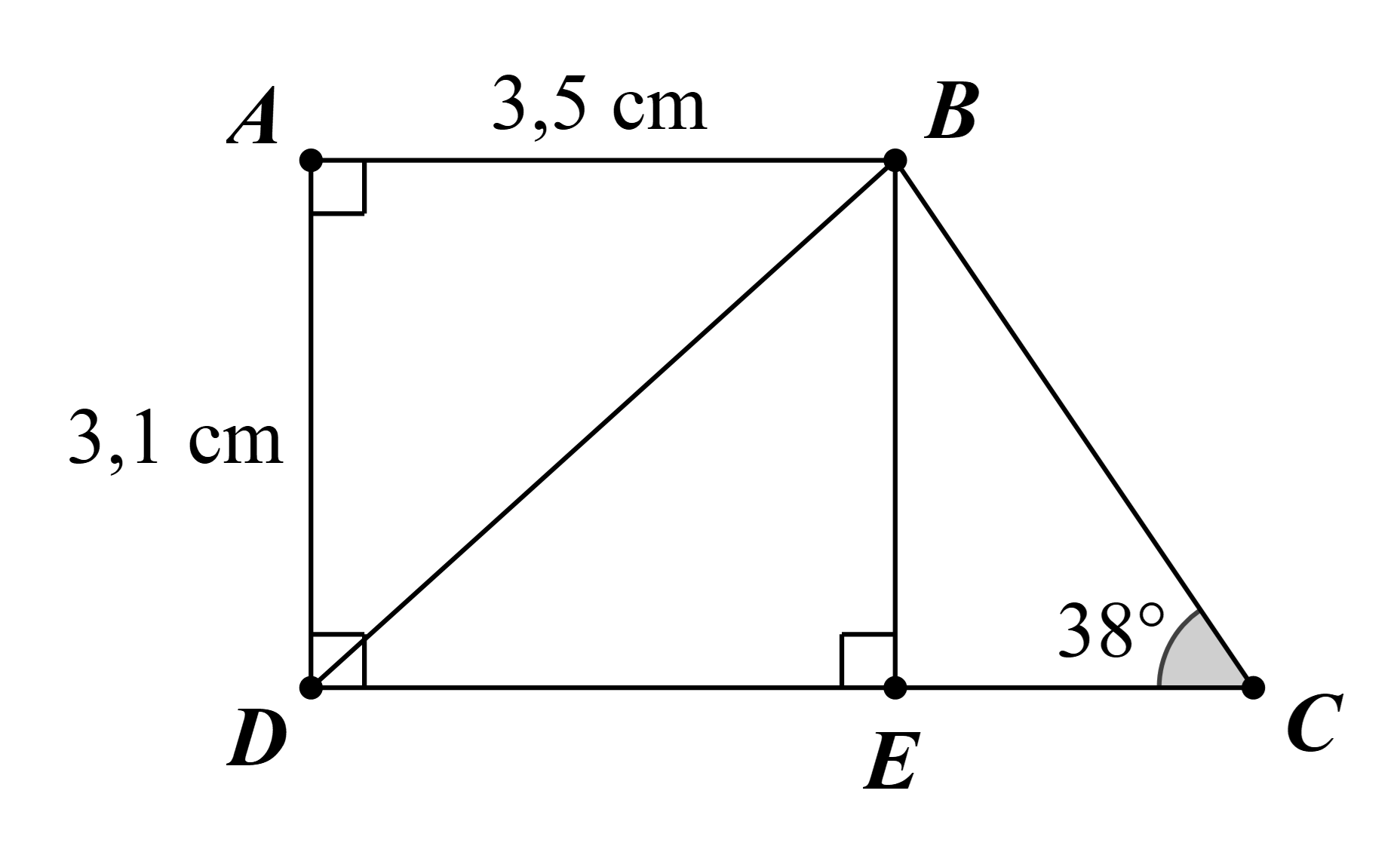
Kẻ BE ⊥ CD tại E.
Ta có AB // CD và AD ⊥ DC.
Suy ra AB ⊥ AD.
Khi đó tứ giác ABED là hình chữ nhật.
Vì vậy DE = AB = 3,5 cm và BE = AD = 3,1 cm.
Tam giác BEC vuông tại E: \(EC = \frac{{BE}}{{\tan \widehat {BCE}}} = \frac{{3,1}}{{\tan 38^\circ }} \approx 3,97\) (cm).
Khi đó DC = DE + EC ≈ 3,5 + 3,97 ≈ 7,47 (cm).
Diện tích hình thang ABCD là:
\(S = \frac{{AD.\left( {AB + DC} \right)}}{2} \approx \frac{{3,1.\left( {3,5 + 7,47} \right)}}{2} \approx 17,0035\) (cm2).
Vậy diện tích hình thang ABCD bằng 17,0035 cm2.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
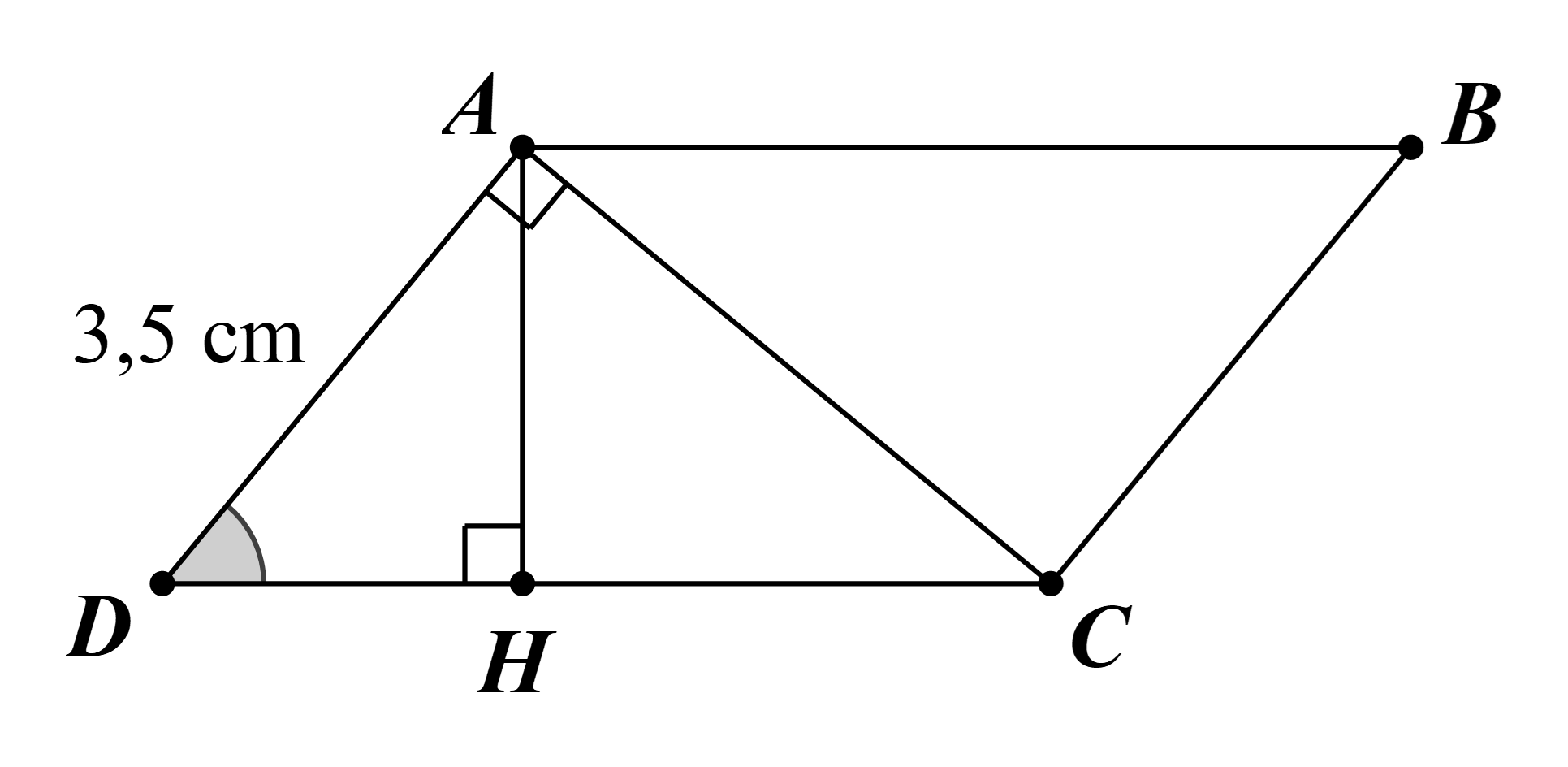
Tam giác ACD vuông tại A: \(CD = \frac{{AD}}{{\cos \widehat {ADC}}} = \frac{{3,5}}{{\cos 60^\circ }} = 7\) (cm).
Kẻ AH ⊥ CD tại H.
Tam giác ADH vuông tại H: \[AH = AD.\sin \widehat {ADH} = 3,5.\sin 60^\circ = \frac{{7\sqrt 3 }}{4}\] (cm).
Diện tích hình bình hành ABCD là: \(S = AH.CD = \frac{{7\sqrt 3 }}{4}.7 = \frac{{49\sqrt 3 }}{4}\) (cm2).
Vậy diện tích hình bình hành ABCD bằng \(\frac{{49\sqrt 3 }}{4}\) cm2.
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Do hạ giá 10% nên giá bán mới bằng 90% giá bình thường.
Coi giá vốn là 100% thì giá bán mới bằng 108% giá vốn.
Như vậy \(\frac{{108}}{{100}}\) (giá vốn) = \(\frac{{90}}{{100}}\) (giá bình thường).
Giá bình thường so với giá vốn là:
\(\frac{{108}}{{100}}:\frac{{90}}{{100}} = \frac{6}{5} = 120\% \).
Nếu không giảm giá thị cửa hàng lãi là:
120% – 100% = 20%.
Đáp số: 20%.
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} - \frac{1}{{2ab}}\)
Áp dụng bất đẳng thức Cauchy, ta được:
\(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} \ge \frac{4}{{{a^2} + {b^2} + 2ab}} = \frac{4}{{{{\left( {a + b} \right)}^2}}} = \frac{4}{{{1^2}}} = 4\) (1)
Áp dụng bất đẳng thức Cauchy, ta được: 4ab ≤ (a + b)2 = 12 = 1.
\( \Rightarrow \frac{2}{{4ab}} \ge \frac{2}{1}\) \( \Rightarrow \frac{1}{{2ab}} \ge 2\) (2)
Lấy (1) trừ (2) vế theo vế, ta được: \(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} - \frac{1}{{2ab}} \ge 4 - 2\).
Vậy \(\frac{1}{{{a^2} + {b^2}}} \ge 2\) (điều phải chứng minh).
Dấu “=” xảy ra \( \Leftrightarrow a = b = \frac{1}{2}\).
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải
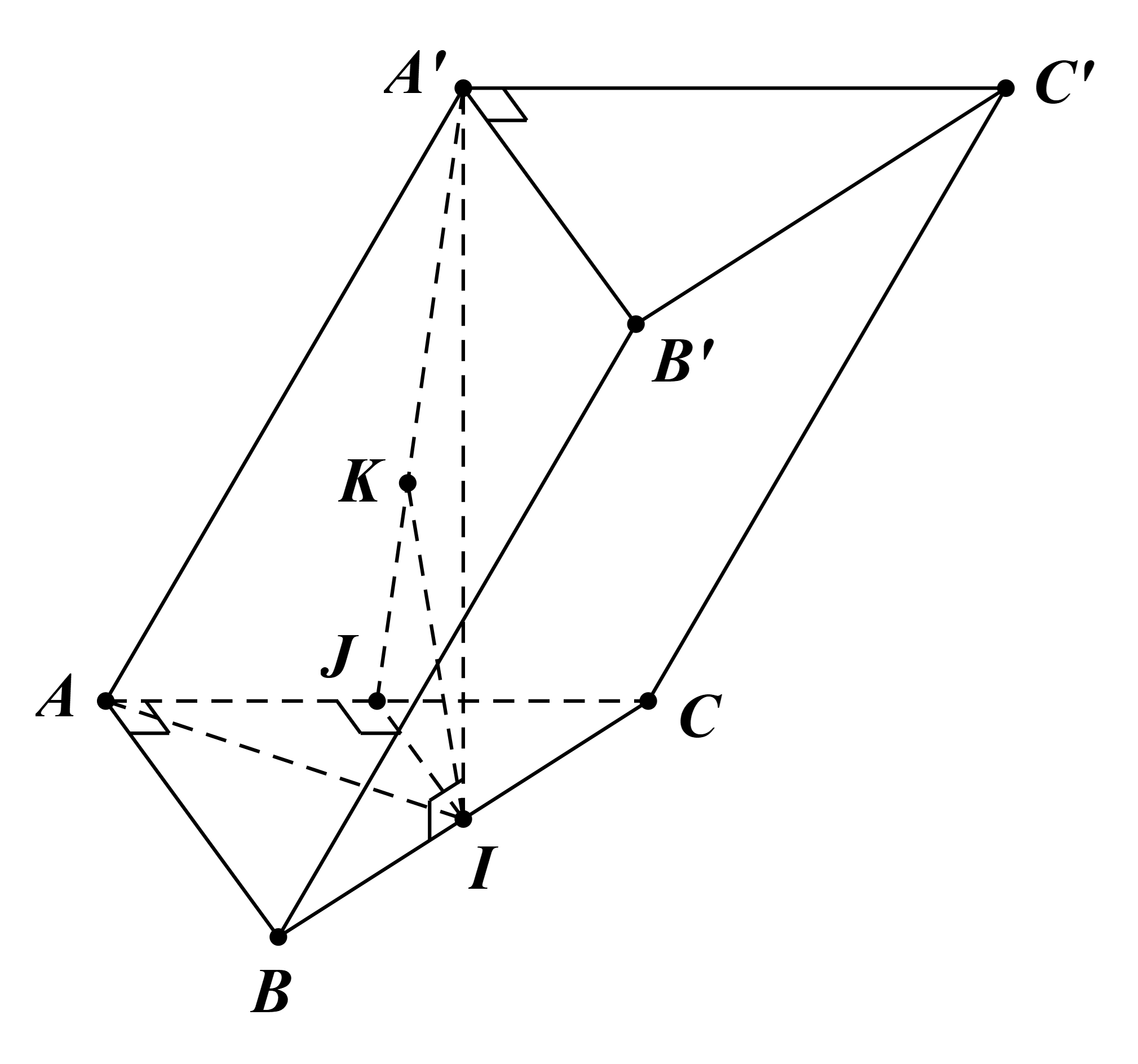
Ta có BB’ // (ACC’A’) và AC’ ⊂ (ACC’A’).
Suy ra d(BB’, AC’) = d(BB’, (ACC’A’)) = d(B, (ACC’A’)).
Gọi J là trung điểm AC.
Khi đó IJ là đường trung bình của tam giác ABC.
Suy ra IJ // AB và \(IJ = \frac{{AB}}{2} = \frac{a}{2}\).
Mà AB ⊥ AC.
Do đó IJ ⊥ AC.
Mà A’I ⊥ AC (do A’I ⊥ (ABC)).
Suy ra AC ⊥ (A’IJ).
Trong (A’IJ): kẻ IK ⊥ A’J tại K.
Khi đó AC ⊥ IK.
Mà IK ⊥ A’J.
Do đó IK ⊥ (ACC’A’).
Vì vậy d(I, (ACC’A’) = IK.
Tam giác ABC vuông tại A có AI là đường trung tuyến.
Suy ra \(AI = IB = IC = \frac{{BC}}{2} = \frac{{\sqrt {A{B^2} + A{C^2}} }}{2} = a\).
Tam giác AA’I vuông tại I: \(A'I = \sqrt {A{{A'}^2} - A{I^2}} = a\sqrt 3 \).
Tam giác A’IJ vuông tại I có IK là đường cao: \[\frac{1}{{I{K^2}}} = \frac{1}{{A'{I^2}}} + \frac{1}{{I{J^2}}} = \frac{{13}}{{3{a^2}}}\].
Suy ra \(IK = \frac{{a\sqrt {39} }}{{13}}\).
Do đó \(d\left( {B,\left( {ACC'A'} \right)} \right) = \frac{{CB}}{{CI}}.d\left( {I,\left( {ACC'A'} \right)} \right) = 2.IK = \frac{{2a\sqrt {39} }}{{13}}\).
Vậy khoảng cách giữa BB’ và AC’ bằng \(\frac{{2a\sqrt {39} }}{{13}}\).
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
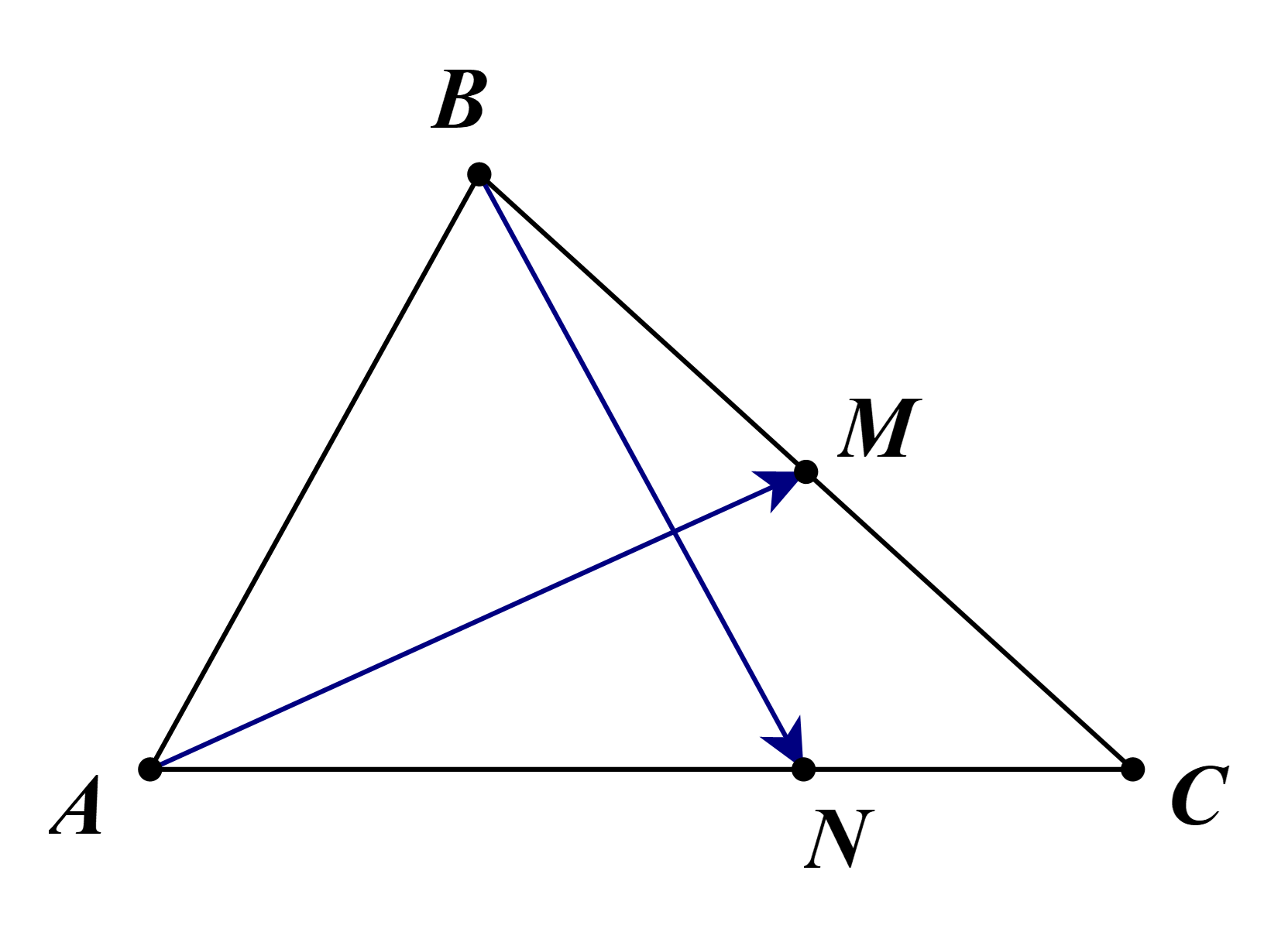
Ta có AC = 3NC. Suy ra \(AN = \frac{2}{3}AC = 6\) và \[\overrightarrow {AN} = \frac{2}{3}\overrightarrow {AC} \].
Tam giác ABC có AM là đường trung tuyến.
Suy ra \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
Ta có \(\overrightarrow {AM} .\overrightarrow {BN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AN} - \overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AN} - A{B^2} + \overrightarrow {AC} .\overrightarrow {AN} - \overrightarrow {AC} .\overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {AB.AN.\cos \widehat {BAC} - A{B^2} + \frac{2}{3}A{C^2} - AC.AB.\cos \widehat {BAC}} \right)\)
\( = \frac{1}{2}\left( {AN.\frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AC}} - A{B^2} + \frac{2}{3}A{C^2} - \frac{{A{B^2} + A{C^2} - B{C^2}}}{2}} \right)\)
\( = \frac{{26}}{3}\).
Vậy ta chọn phương án A.
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\overrightarrow {AB} .\overrightarrow {CB} = AB.CB.\cos \widehat B = AB.CB.\frac{{AB}}{{BC}} = A{B^2} = 4\).
Suy ra AB = 2.
Lại có \(\overrightarrow {AC} .\overrightarrow {BC} = AC.BC.\cos \widehat C = AC.BC.\frac{{AC}}{{BC}} = A{C^2} = 9\).
Suy ra AC = 3.
Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \).
Vậy AB = 2; AC = 3; \(BC = \sqrt {13} \).
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \( - \frac{b}{{2a}} = - \frac{{4m}}{{2.\left( { - 4} \right)}} = \frac{m}{2}\).
Mà a = –4 < 0.
Suy ra hàm số đã cho nghịch biến trên \(\left( {\frac{m}{2}; + \infty } \right)\).
Theo đề, ta có hàm số đã cho nghịch biến trên (–2; +∞).
\[ \Leftrightarrow \left( { - 2; + \infty } \right) \subset \left( {\frac{m}{2}; + \infty } \right)\].
\[ \Leftrightarrow \frac{m}{2} \le - 2\].
⇔ m ≤ –4.
Vậy m ≤ –4 thỏa mãn yêu cầu bài toán.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Vì x, y ∈ ℤ và (5x + 1)(y – 1) = 4 nên ta có bảng sau:
|
5x + 1 |
–4 |
–2 |
–1 |
1 |
2 |
4 |
|
y – 1 |
–1 |
–2 |
–4 |
4 |
2 |
1 |
|
x |
–1 |
\( - \frac{3}{5}\) |
\( - \frac{2}{5}\) |
0 |
\(\frac{1}{5}\) |
\(\frac{3}{5}\) |
|
y |
0 |
–1 |
–3 |
5 |
3 |
2 |
|
|
Nhận |
Loại |
Loại |
Nhận |
Loại |
Loại |
Vậy (x; y) ∈ {(–1; 0), (0; 5)}.
Câu 11:
 Xem đáp án
Xem đáp án
Lời giải
C = (x – 2)(x2 + 2x + 4) – x2(x + 2).
= x3 – 23 – x3 – 2x2.
= –2x2 – 8.
Câu 12:
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.
a) Chứng minh AD = BC.
b) Gọi E là giao điểm của AD và BC. Chứng minh ∆EAC = ∆EBD.
c) Chứng minh OE là phân giác của \(\widehat {xOy}\).
 Xem đáp án
Xem đáp án
Lời giải
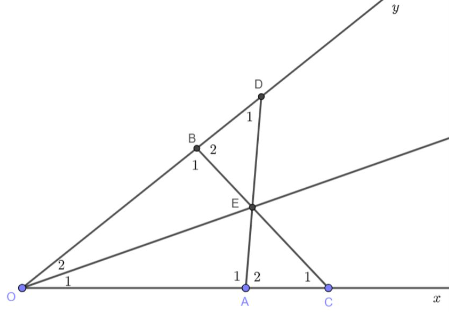
a) Ta có OA = OB và AC = BD.
Suy ra OA + AC = OB + BD.
Do đó OC = OD.
Xét ∆OAD và ∆OBC, có:
\(\widehat {AOD}\) là góc chung;
OA = OB (giả thiết);
OD = OC (chứng minh trên).
Do đó ∆OAD = ∆OBC (c.g.c).
Vậy AD = BC (cặp cạnh tương ứng).
b) Ta có \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) và \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (các cặp góc kề bù).
Mà \(\widehat {{A_1}} = \widehat {{B_1}}\) (do ∆OAD = ∆OBC).
Suy ra \(\widehat {{A_2}} = \widehat {{B_2}}\).
Xét ∆EAC và ∆EBD, có:
AC = BD (giả thiết);
\(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh trên);
\(\widehat {{C_1}} = \widehat {{D_1}}\) (do ∆OAD = ∆OBC).
Vậy ∆EAC = ∆EBD (g.c.g).
c) Xét ∆OED và ∆OEC, có:
OE là cạnh chung;
OD = OC (chứng minh trên);
ED = EC (do ∆EAC = ∆EBD).
Do đó ∆OED = ∆OEC (c.c.c).
Suy ra \(\widehat {{O_1}} = \widehat {{O_2}}\) (cặp góc tương ứng).
Vậy OE là phân giác của \(\widehat {xOy}\).
Câu 13:
 Xem đáp án
Xem đáp án
Lời giải
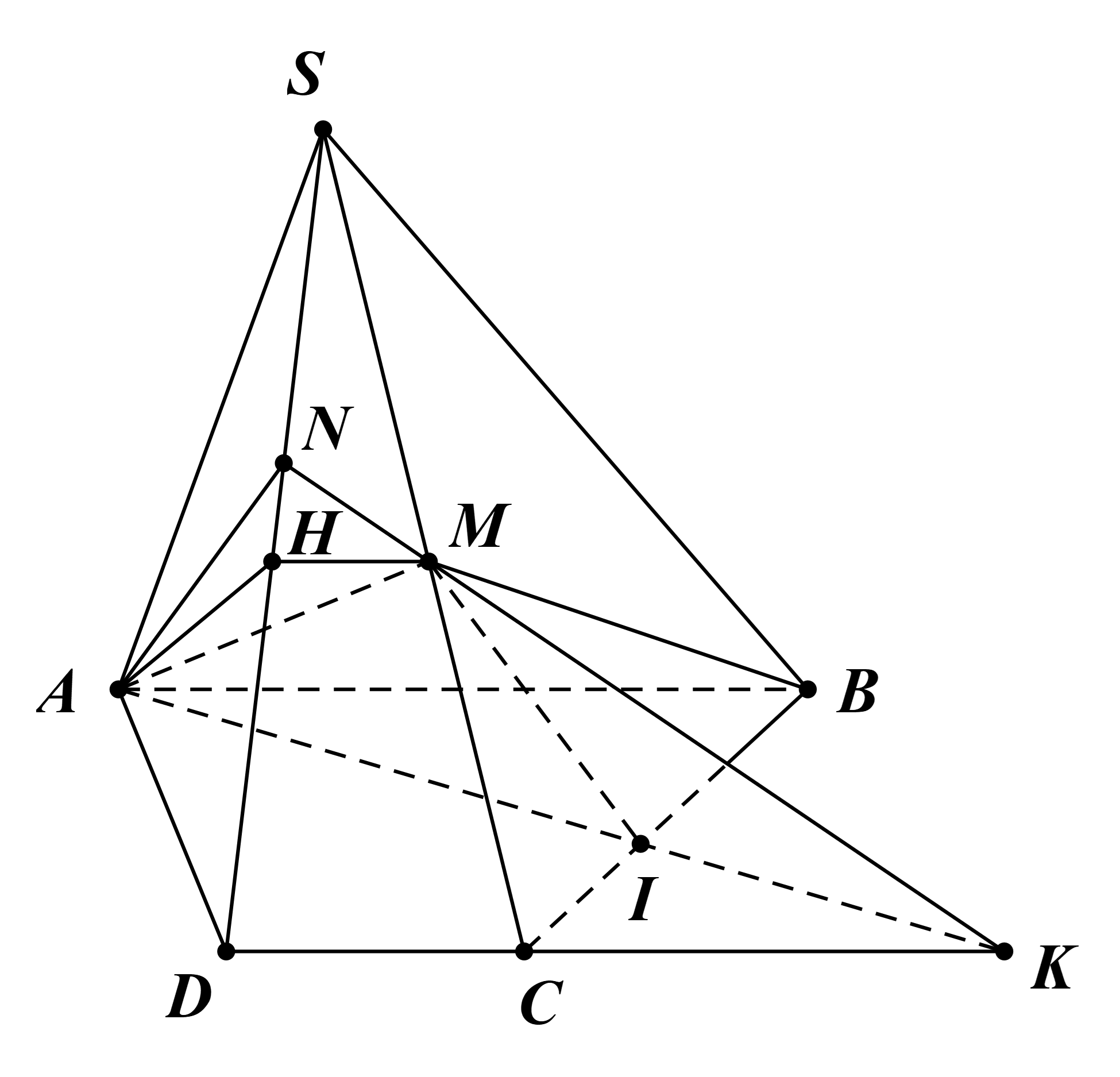
⦁ Thiết diện của hình chóp với (ABM):
Ta có M ∈ (ABM) ∩ (SCD).
Mà AB // CD.
Suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng d đi qua M và d // AB // CD.
Trong (SCD): gọi H = d ∩ SD.
Suy ra MH = (ABM) ∩ (SCD).
Ta có:
+ (ABM) ∩ (ABCD) = AB.
+ (ABM) ∩ (SBC) = BM.
+ (ABM) ∩ (SCD) = MH.
+ (ABM) ∩ (SAD) = HA.
Vậy thiết diện của hình chóp với (ABM) là tứ giác ABMH.
⦁ Thiết diện của hình chóp với (AMN):
Trong (SCD): gọi K = MN ∩ CD.
Trong (ABCD): gọi I = AK ∩ BC.
Ta có:
+ (AMN) ∩ (SAD) = AN.
+ (AMN) ∩ (SCD) = MN.
+ (AMN) ∩ (SBC) = MI.
+ (AMN) ∩ (ABCD) = IA.
Vậy thiết diện của hình chóp với (AMN) là tứ giác ANMI.
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
Gọi A(x; y).
Suy ra \(\overrightarrow {AB} = \left( { - 2 - x;3 - y} \right),\,\overrightarrow {AC} = \left( {3 - x;1 - y} \right)\)
Tam giác ABC vuông cân tại A.
\[ \Rightarrow \left\{ \begin{array}{l}AB \bot AC\\AB = AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = 0\\A{B^2} = A{C^2}\end{array} \right.\]
\[ \Rightarrow \left\{ \begin{array}{l}\left( { - 2 - x} \right)\left( {3 - x} \right) + \left( {3 - y} \right)\left( {1 - y} \right) = 0\\{\left( { - 2 - x} \right)^2} + {\left( {3 - y} \right)^2} = {\left( {3 - x} \right)^2} + {\left( {1 - y} \right)^2}\end{array} \right.\]
\[ \Rightarrow \left\{ \begin{array}{l} - x + {x^2} - 3 - 4y + {y^2} = 0\,\,\,\,\,\left( 1 \right)\\\frac{{10x + 3}}{4} = y\end{array} \right.\]
Thế \[\frac{{10x + 3}}{4} = y\] vào (1), ta được: \[ - x + {x^2} - 3 - 10x - 3 + {\left( {\frac{{10x + 3}}{4}} \right)^2} = 0\].
⇔ 116x2 – 116x – 87 = 0.
\( \Leftrightarrow x = \frac{3}{2}\) hoặc \(x = - \frac{1}{2}\).
Với \(x = \frac{3}{2}\), ta có: \(y = \frac{9}{2}\). Suy ra tọa độ \(A\left( {\frac{3}{2};\frac{9}{2}} \right)\).
Với \(x = - \frac{1}{2}\), ta có: \(y = - \frac{1}{2}\). Suy ra tọa độ \(A\left( { - \frac{1}{2}; - \frac{1}{2}} \right)\).
Vậy có hai điểm A thỏa mãn yêu cầu bài toán có tọa độ là \(A\left( {\frac{3}{2};\frac{9}{2}} \right)\) và \(A\left( { - \frac{1}{2}; - \frac{1}{2}} \right)\).
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
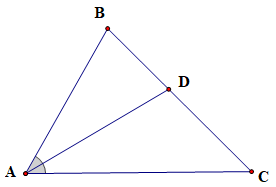
Tam giác ABC có AD là tia phân giác.
Suy ra \(\widehat {BAD} = \widehat {CAD} = \frac{{\widehat {BAC}}}{2} = 30^\circ \).
Ta có SABC = SABD + SACD.
\( \Leftrightarrow \frac{1}{2}AB.AC.\sin \widehat {BAC} = \frac{1}{2}AB.AD.\sin \widehat {BAD} + \frac{1}{2}AC.AD.\sin \widehat {CAD}\).
⇔ AB.AC.sin60° = AB.AD.sin30° + AC.AD.sin30°.
\( \Leftrightarrow \frac{{\sqrt 3 AB.AC}}{2} = \frac{{AB.AD}}{2} + \frac{{AC.AD}}{2}\).
\( \Leftrightarrow \sqrt 3 AB.AC = AD.\left( {AB + AC} \right)\).
Vậy \(AD = \frac{{\sqrt 3 AB.AC}}{{AB + AC}}\) (điều phải chứng minh).
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải

Xét tam giác AMN, có: AM = AN.
Suy ra tam giác AMN cân tại A.
Do đó đường trung tuyến AE của tam giác AMN cũng là phân giác của \(\widehat {MAN}\) (1)
Xét tam giác ABC, có: AB = AC.
Suy ra tam giác ABC cân tại A.
Do đó đường trung tuyến AD của tam giác ABC cũng là phân giác của \(\widehat {BAC}\) (2)
Từ (1), (2), suy ra D, E cùng thuộc tia phân giác của \(\widehat A\).
Vậy ba điểm A, E, D thẳng hàng.
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải

Gọi N là trung điểm của AC.
Suy ra MN là đường trung bình của tam giác ABC.
Do đó MN // AB và \(MN = \frac{{AB}}{2} = \frac{{\sqrt {O{A^2} + O{B^2}} }}{2} = \frac{{\sqrt {4O{C^2} + 4O{C^2}} }}{2} = \sqrt 2 OC\).
Khi đó góc giữa hai đường thẳng OM và AB là góc giữa hai đường thẳng OM và MN và bằng \(\widehat {OMN}\).
Tam giác OAC vuông tại O có ON là đường trung tuyến.
Suy ra \(ON = AN = NC = \frac{{AC}}{2} = \frac{{\sqrt {O{A^2} + O{C^2}} }}{2} = \frac{{OC\sqrt 5 }}{2}\).
Ta có \(B{C^2} = O{B^2} + O{C^2} - 2OB.OC.\cos \widehat {BOC} = 5O{C^2} - 4O{C^2}.\cos 60^\circ = 3O{C^2}\).
Khi đó \(O{M^2} = \frac{{2\left( {O{B^2} + O{C^2}} \right) - B{C^2}}}{4} = \frac{{2\left( {4O{C^2} + O{C^2}} \right) - 3O{C^2}}}{4} = \frac{{7O{C^2}}}{4}\).
Ta có \(\cos \widehat {OMN} = \frac{{O{M^2} + M{N^2} - O{N^2}}}{{2.OM.MN}} = \frac{{\frac{{7O{C^2}}}{4} + 2O{C^2} - \frac{{5O{C^2}}}{4}}}{{2.\frac{{OC\sqrt 7 }}{2}.\sqrt 2 OC}} = \frac{{5\sqrt {14} }}{{28}}\).
Vậy côsin giữa hai đường thẳng OM và AB bằng \(\frac{{5\sqrt {14} }}{{28}}\).
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải

Giả sử ta có tam giác vuông như hình vẽ.
Với góc α < 90°, ta có b là cạnh kề, a là cạnh đối, h là cạnh huyền.
Với góc β < 90°, ta có a là cạnh kề, b là cạnh đối, h là cạnh huyền.
Tóm lại:
Cạnh huyền là cạnh đối diện góc vuông.
Cạnh kề là cạnh góc vuông kề với góc đó.
Cạnh đối là cạnh góc vuông đối diện với góc đó.
Câu 19:
a) Viết phương trình đường thẳng biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và cắt trục hoành tại điểm có hoành độ bằng –3.
b) Viết phương trình đường thẳng (d) biết (d) có hệ số góc là –2 và đi qua điểm A(–1; 5).
 Xem đáp án
Xem đáp án
Lời giải
a) Phương trình đường thẳng cần tìm có dạng: y = ax + b (a ≠ 0).
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 4 nên 4 = a.0 + b ⇔ b = 4.
Vì đường thẳng cắt trục hoành tại điểm có hoành độ bằng –3 nên 0 = –3a + b.
⇔ –3a + 4 = 0.
\( \Leftrightarrow a = \frac{4}{3}\) (nhận).
Vậy phương trình đường thẳng cần tìm là \(y = \frac{4}{3}x + 4\).
b) Phương trình đường thẳng (d) cần tìm có dạng: y = ax + b (a ≠ 0).
Đường thẳng (d) có hệ số góc là –2 nên ta có a = –2.
Vì (d) đi qua điểm A(–1; 5) nên 5 = a.(–1) + b.
⇔ 5 = 2 + b.
⇔ b = 3.
Vậy phương trình đường thẳng (d): y = –2x + 3.
Câu 20:
Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0).
a) Tìm m để đồ thị hàm số (1) đi qua điểm M(1; 3).
b) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 4. Vẽ đồ thị hàm số với m tìm được.
 Xem đáp án
Xem đáp án
Lời giải
a) Vì đồ thị hàm số (1) đi qua điểm M(1; 3) nên 3 = (m – 1).1 + m.
⇔ 3 = m – 1 + m.
⇔ m = 1.
Vậy m = 1 thỏa mãn yêu cầu bài toán.
b) Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 4 nên 4 = (m – 1).0 + m.
⇔ m = 4.
Vậy m = 4 thỏa mãn yêu cầu bài toán.
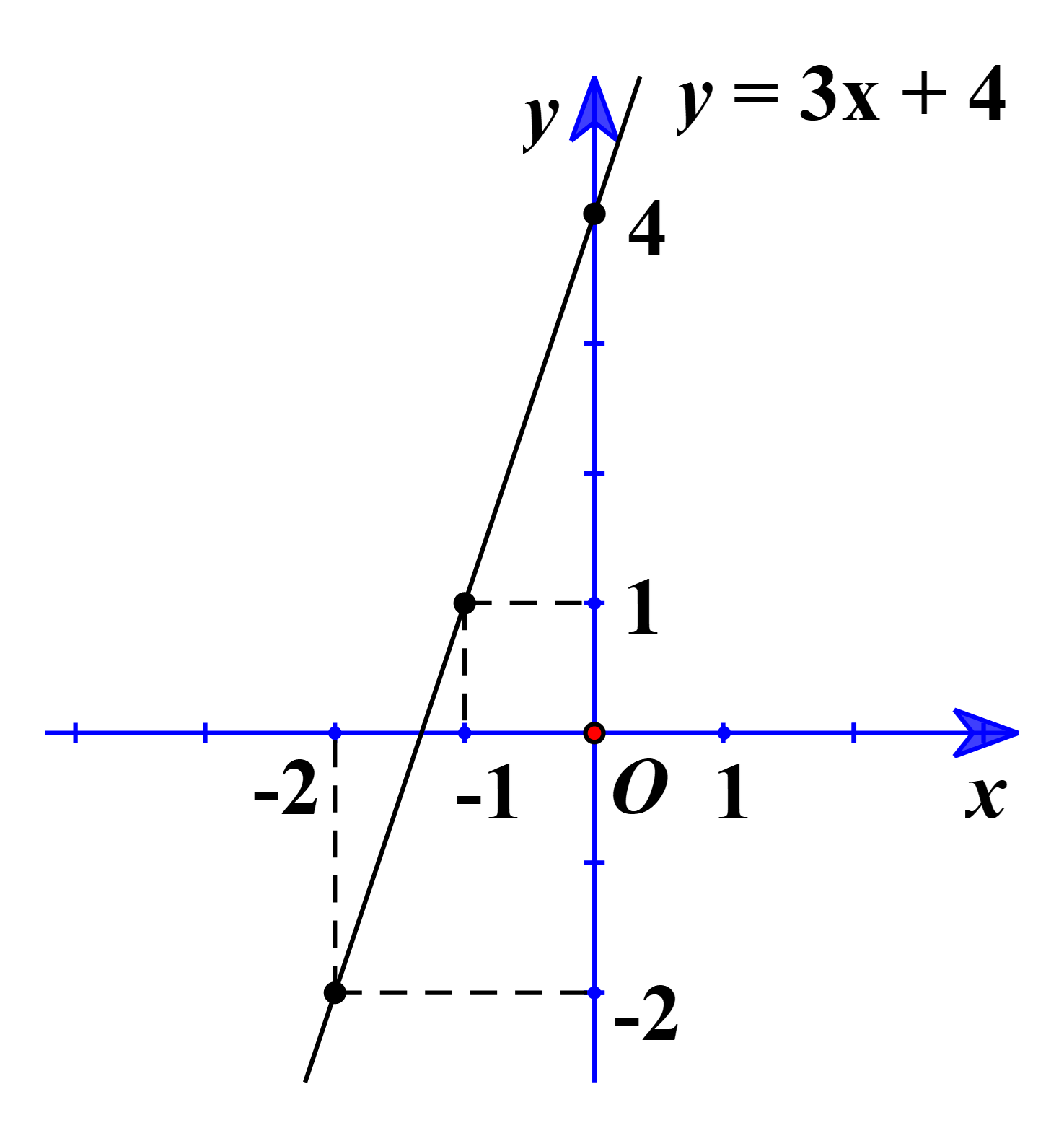
Với m = 4, ta có y = 3x + 4.
Bảng giá trị:
|
x |
–2 |
–1 |
0 |
|
y |
–2 |
1 |
4 |
Đồ thị hàm số y = 3x + 4:
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
Theo định lí Bezout thì dư của phép chia đa thức f(x) = 1 + x2 + x4 + x6 + ... + x100 cho x + 1 là f(–1).
Ta có f(–1) = 1 + (–1)2 + (–1)4 + (–1)6 + ... + (–1)100 = 1 + 1 + 1 + 1 + ... + 1 = 51.
Vậy dư trong phép chia đa thức f(x) = 1 + x2 + x4 + x6 + ... + x100 cho x + 1 là 51.
Câu 22:
 Xem đáp án
Xem đáp án
Lời giải
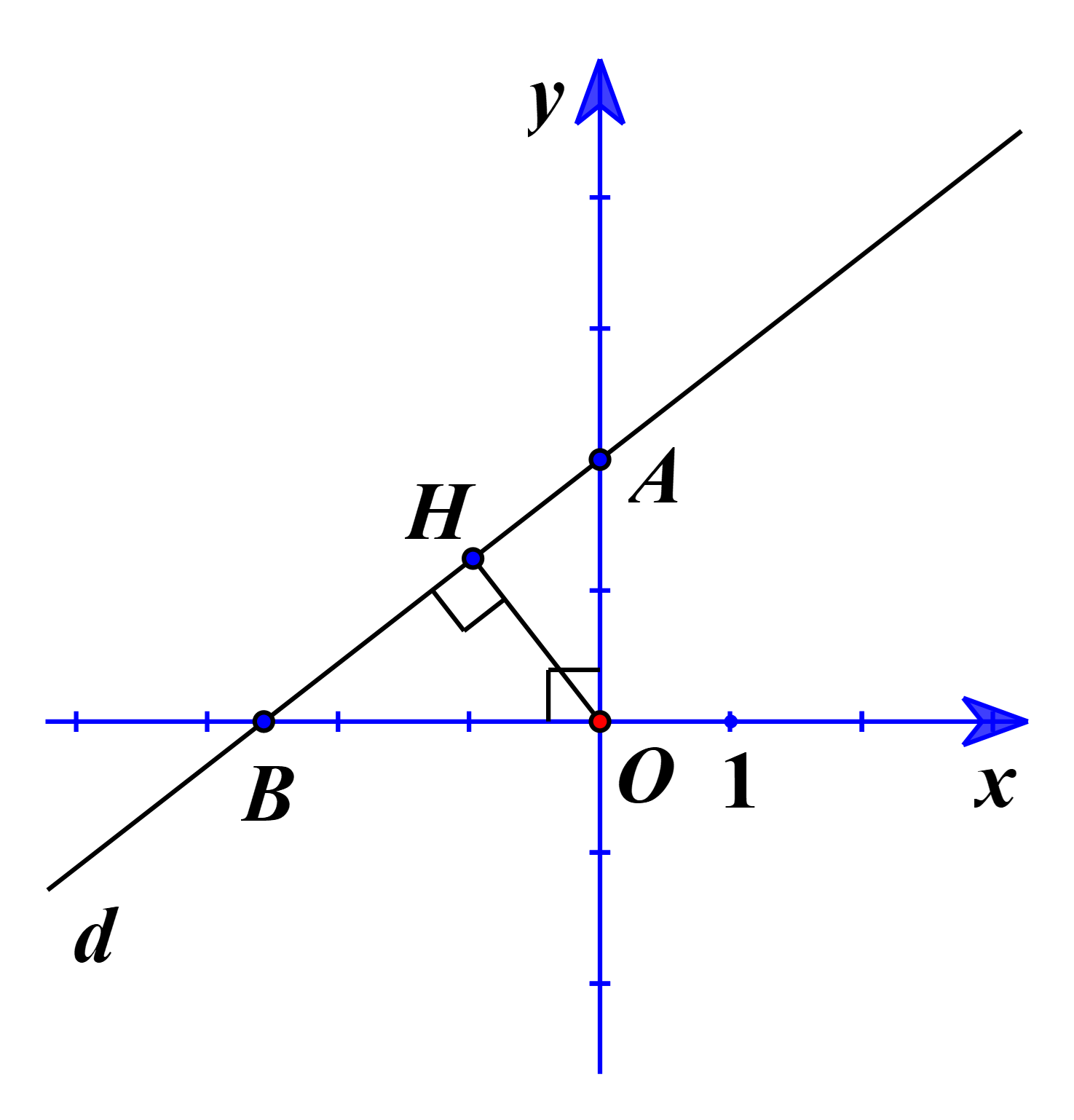
Gọi A, B lần lượt là giao điểm của đường thẳng d với các trục Oy, Ox.
Với x = 0, ta có: y = 2. Suy ra tọa độ A(0; 2).
Với y = 0, ta có: \(x = - \frac{2}{{m - 1}}\). Suy ra tọa độ \(B\left( { - \frac{2}{{m - 1}};0} \right)\).
Kẻ OH vuông góc với AB.
Khi đó khoảng cách từ gốc tọa độ O đến đường thẳng d là lớn nhất.
⇔ OH lớn nhất.
⇔ OH2 lớn nhất.
Ta có OA = 2, \[OB = \left| { - \frac{2}{{m - 1}}} \right|\].
Tam giác OAB vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{4} + \frac{{{{\left( {m - 1} \right)}^2}}}{4} = \frac{{{{\left( {m - 1} \right)}^2} + 1}}{4}\).
Suy ra \(O{H^2} = \frac{4}{{{{\left( {m - 1} \right)}^2} + 1}}\).
Ta có: (m – 1)2 + 1 ≥ 1, ∀m.
\( \Rightarrow O{H^2} = \frac{4}{{{{\left( {m - 1} \right)}^2} + 1}} \le 4,\,\,\forall m\).
Dấu “=” xảy ra ⇔ m = 1.
Vậy m = 1 thỏa mãn yêu cầu bài toán.
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
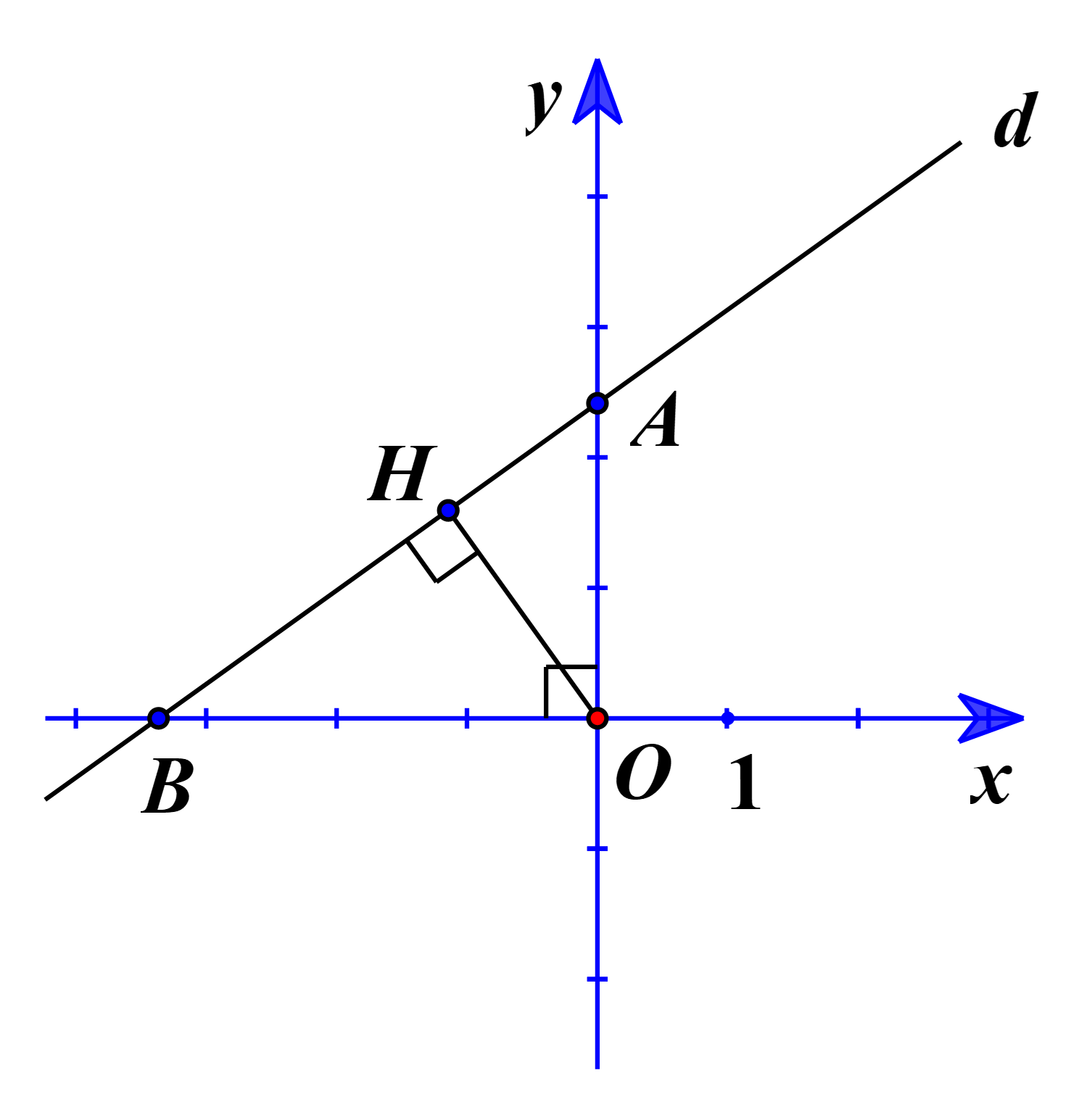
Gọi A, B lần lượt là giao điểm của đường thẳng d với các trục Oy, Ox.
Với x = 0, ta có: y = –m + 1. Suy ra tọa độ A(0; –m + 1).
Với y = 0, ta có: \(x = \frac{{m - 1}}{m}\). Suy ra tọa độ \(B\left( {\frac{{m - 1}}{m};0} \right)\).
Kẻ OH vuông góc với AB.
Khi đó khoảng cách từ gốc tọa độ O đến đường thẳng d là lớn nhất.
⇔ OH lớn nhất.
Ta có OA = |–m + 1|, \[OB = \left| {\frac{{m - 1}}{m}} \right|\].
Tam giác OAB vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{{{{\left( {m - 1} \right)}^2}}} + \frac{{{m^2}}}{{{{\left( {m - 1} \right)}^2}}} = \frac{{{m^2} + 1}}{{{{\left( {m - 1} \right)}^2}}}\).
Suy ra \(O{H^2} = \frac{{{{\left( {m - 1} \right)}^2}}}{{{m^2} + 1}}\).
Do đó \(OH = \frac{{\left| {m - 1} \right|}}{{\sqrt {{m^2} + 1} }}\).
Áp dụng bất đẳng thức Bunhiaxcopki, ta có: \(\frac{{\left| {m - 1} \right|}}{{\sqrt {{m^2} + 1} }} \le \sqrt {2.\frac{{{m^2} + 1}}{{{m^2} + 1}}} = \sqrt 2 \).
Dấu “=” xảy ra ⇔ m = –1.
Vậy m = –1 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 24:
Cho phương trình mx2 – (2m + 1)x + (m + 1) = 0 (1)
a) Giải phương trình (1) với \(m = \frac{{ - 3}}{5}\).
b) Chứng minh rằng phương trình (1) luông có nghiệm với mọi giá trị của m.
c) Tìm các giá trị của m để phương trình (1) có nghiệm lớn hơn 2.
 Xem đáp án
Xem đáp án
Lời giải
a) Thế \(m = \frac{{ - 3}}{5}\) vào phương trình (1) ta được: \(\frac{{ - 3}}{5}{x^2} + \frac{1}{5}x + \frac{2}{5} = 0\).
⇔ –3x2 + x + 2 = 0.
⇔ (3x + 2)(x – 1) = 0.
\( \Leftrightarrow \left[ \begin{array}{l}3x + 2 = 0\\x - 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - \frac{2}{3}\\x = 1\end{array} \right.\)
Vậy với \(m = \frac{{ - 3}}{5}\) thì tập nghiệm của phương trình đã cho là \(S = \left\{ { - \frac{2}{3};1} \right\}\).
b) Ta có ∆ = (2m + 1)2 – 4m(m + 1) = 4m2 + 4m + 1 – 4m2 – 4m = 1 > 0, ∀m.
Vậy phương trình (1) luôn có nghiệm, với mọi giá trị của m.
c) Hai nghiệm của phương trình (1) là: \(\left[ \begin{array}{l}{x_1} = \frac{{2m + 1 + 1}}{{2m}} = \frac{{m + 1}}{m}\\{x_2} = \frac{{2m + 1 - 1}}{{2m}} = 1\end{array} \right.\)
Vì x2 = 1 < 2 nên để phương trình (1) có nghiệm lớn hơn 2 thì x1 > 2.
Tức là, \(\frac{{m + 1}}{m} > 2\).
\( \Leftrightarrow \frac{{ - m + 1}}{m} > 0\).
\( \Leftrightarrow \left\{ \begin{array}{l} - m + 1 > 0\\m > 0\end{array} \right.\) hoặc \(\left\{ \begin{array}{l} - m + 1 < 0\\m < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m > 0\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}m > 1\\m < 0\end{array} \right.\) (vô lí).
⇔ 0 < m < 1.
Vậy 0 < m < 1 thỏa mãn yêu cầu bài toán.
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Hàm số đã cho xác định \( \Leftrightarrow \left\{ \begin{array}{l}x - m \ge 0\\2x - m - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m\\x \ge \frac{{m + 1}}{2}\end{array} \right.\,\,\,\,\,\,\left( * \right)\)
Trường hợp 1: \(m \ge \frac{{m + 1}}{2} \Leftrightarrow m \ge 1\).
Khi đó (*) ⇔ x ≥ m.
Suy ra tập xác định của hàm số đã cho là D = [m; +∞).
Vì vậy hàm số đã cho xác định trên (0; +∞) khi và chỉ khi (0; +∞) ⊂ [m; +∞).
⇔ m ≤ 0 (mâu thuẫn vì m ≥ 1).
Trường hợp 2: \(m \le \frac{{m + 1}}{2} \Leftrightarrow m \le 1\).
Khi đó \(\left( * \right) \Leftrightarrow x \ge \frac{{m + 1}}{2}\).
Suy ra tập xác định của hàm số đã cho là \(D = \left[ {\frac{{m + 1}}{2}; + \infty } \right)\).
Vì vậy hàm số đã cho xác định trên (0; +∞) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {\frac{{m + 1}}{2}; + \infty } \right)\).
\( \Leftrightarrow \frac{{m + 1}}{2} \le 0 \Leftrightarrow m \le - 1\).
So với điều kiện m ≤ 1, ta nhận m ≤ –1.
Vậy m ≤ –1 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\frac{2}{3} - \frac{5}{3}x = \frac{7}{{10}}x + \frac{5}{6}\)
\( - \frac{5}{3}x - \frac{7}{{10}}x = \frac{5}{6} - \frac{2}{3}\)
\( - \frac{{71}}{{30}}x = \frac{1}{6}\)
\(x = \frac{1}{6}:\left( { - \frac{{71}}{{30}}} \right)\)
\(x = - \frac{5}{{71}}\)
Vậy \(x = - \frac{5}{{71}}\).
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Vì A, B khác rỗng nên ta có \(\left\{ \begin{array}{l}m - 1 < 5\\3 < 2020 - 5m\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 6\\5m < 2017\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 6\\m < \frac{{2017}}{5}\end{array} \right.\)
⇔ m < 6.
Để A \ B = ∅ thì A ⊂ B.
\( \Leftrightarrow \left\{ \begin{array}{l}3 \le m - 1\\5 < 2020 - 5m\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ge 4\\m < 403\end{array} \right.\)
⇔ 4 ≤ m < 403.
So với điều kiện m < 6, ta nhận 4 ≤ m < 6.
Mà m ∈ ℤ nên m ∈ {4; 5}.
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 28:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
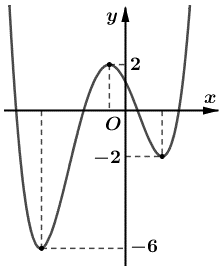
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
 Xem đáp án
Xem đáp án
Lời giải
Quan sát đồ thị, ta thấy hàm số y = f(x) có 3 điểm cực trị.
Do đó để hàm số y = |f(x) – m + 2018| có 7 điểm cực trị thì đồ thị hàm số y = f(x) cắt đường thẳng y = m – 2018 tại 7 – 3 = 4 điểm phân biệt khác 3 điểm cực trị của hàm số y = f(x).
⇔ –2 < m – 2018 < 2.
⇔ 2016 < m < 2020.
Mà m ∈ ℤ.
Suy ra m ∈ {2017; 2018; 2019}.
Vậy có 3 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
Câu 29:
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC.
a) Chứng minh rằng BE = CD.
b) Chứng minh BE // CD.
c) Gọi M là trung điểm của BE và N là trung điểm của CD. Chứng minh AM = AN.
 Xem đáp án
Xem đáp án
Lời giải
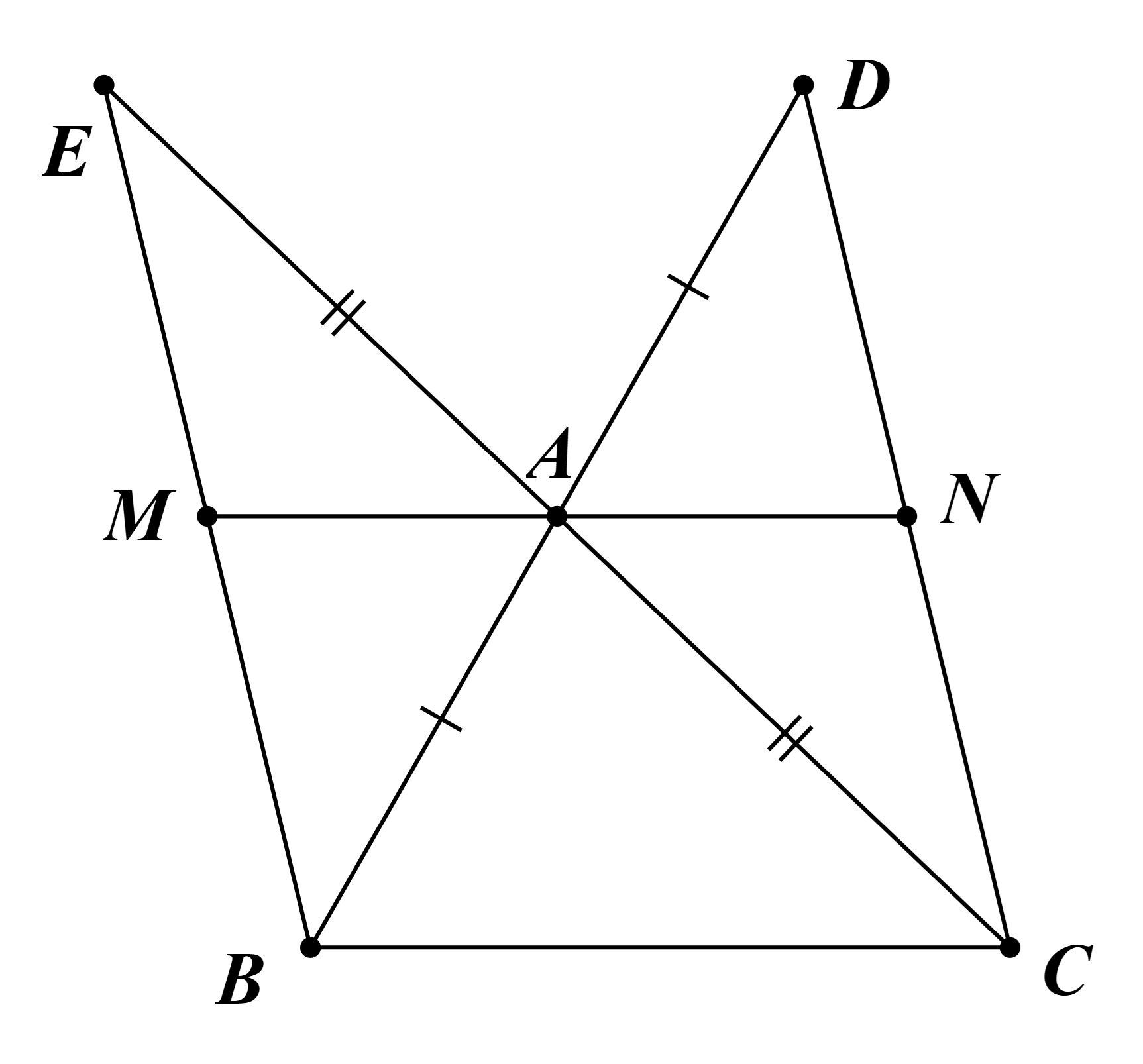
a) Xét ∆ABE và ∆ADC, có:
AB = AD (giả thiết);
AE = AC (giả thiết);
\(\widehat {BAE} = \widehat {CAD}\) (đối đỉnh).
Do đó ∆ABE = ∆ADC (c.g.c).
Vậy BE = CD (cặp cạnh tương ứng).
b) Ta có \(\widehat {ABE} = \widehat {ADC}\) (do ∆ABE = ∆ADC).
Mà hai góc này ở vị trí so le trong.
Vậy BE // CD.
c) Ta có M là trung điểm của BE.
Suy ra BE = 2BM.
Chứng minh tương tự, ta được: CD = 2DN.
Mà BE = CD (kết quả câu a).
Suy ra 2BM = 2DN.
Do đó BM = DN.
Xét ∆ABM và ∆ADN, có:
AB = AD (giả thiết);
BM = DN (chứng minh trên);
\(\widehat {ABM} = \widehat {ADN}\) (chứng minh trên).
Do đó ∆ABM = ∆ADN (c.g.c).
Vậy AM = AN (cặp cạnh tương ứng).
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
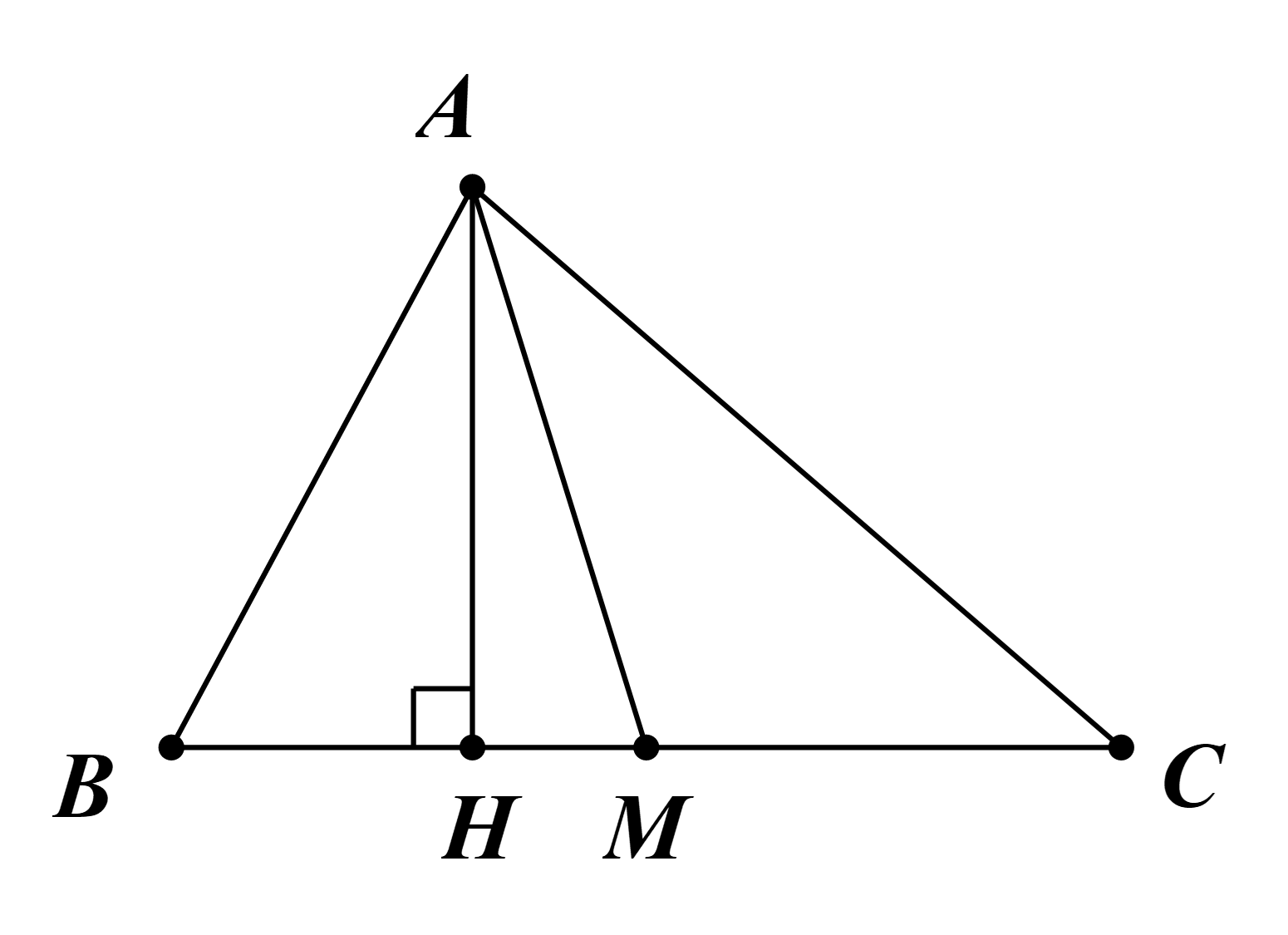
Kẻ đường cao AH của tam giác ABC.
Ta có \({S_{AMB}} = \frac{1}{2}AH.MB\) và \({S_{AMC}} = \frac{1}{2}AH.MC\).
Mà MB = MC (do AM là đường trung tuyến của tam giác ABC).
Vậy SAMB = SAMC (điều phải chứng minh).
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
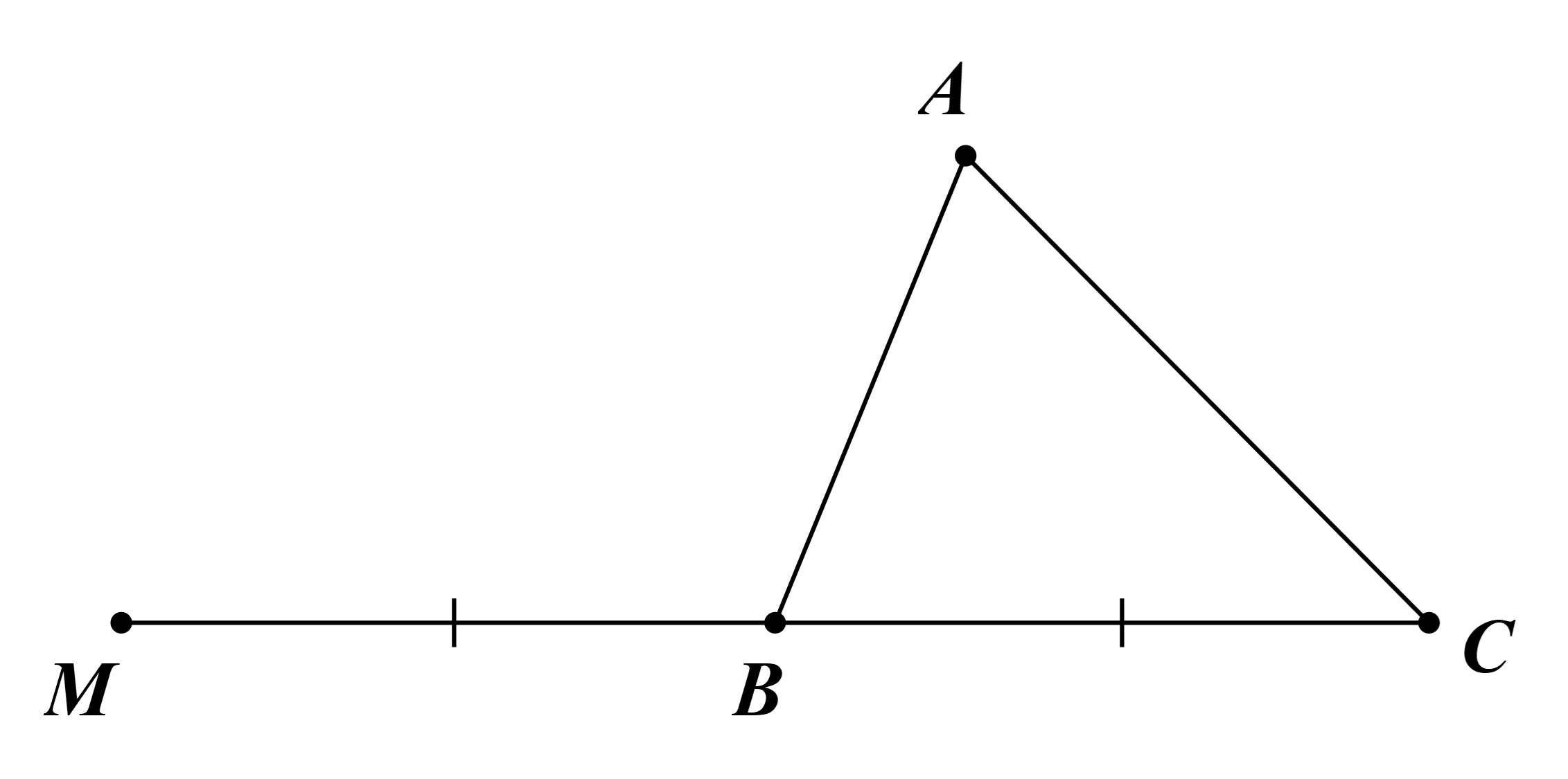
Ta có \(\overrightarrow {AB} + \overrightarrow {MA} = \overrightarrow {MC} + \overrightarrow {BM} \).
\( \Leftrightarrow \overrightarrow {MB} = \overrightarrow {BC} \).
\( \Leftrightarrow \overrightarrow {BM} + \overrightarrow {BC} = \vec 0\).
Suy ra B là trung điểm của MC.
Vậy M là điểm đối xứng với điểm C qua điểm B.
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
Gọi chữ số cần lập là \[\overline {abcde} \].
Trường hợp 1: có mặt chữ số 0.
Chọn 3 chữ số còn lại (ngoài hai số 0 và 5) thì có \(C_5^3 = 10\) cách.
Hoán vị 5 chữ số và loại đi trường hợp a = 0 thì có 5! – 4! cách.
Suy ra ta có tất cả 10.(5! – 4!) = 960 số thỏa mãn trường hợp 1.
Trường hợp 2: không có mặt chữ số 0.
Chọn 4 chữ số còn lại thì có \(C_5^4 = 5\) cách.
Hoán vị 5 chữ số thì có 5! cách.
Suy ra ta có tất cả 5.5! = 600 số thỏa mãn trường hợp 2.
Vậy ta có tất cả 960 + 600 = 1560 số thỏa mãn yêu cầu bài toán.
Câu 33:
 Xem đáp án
Xem đáp án
Lời giải
Ta có nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không đổi.
Khi đó chiều rộng thành chiều dài và chiều dài thành chiều rộng. Chiều dài hơn chiều rộng 5 m.
Chiều dài hình chữ nhật là:
(99 + 5) : 2 = 52 (m).
Chiều rộng hình chữ nhật là:
(99 – 5) : 2 = 47 (m).
Diện tích hình chữ nhật là:
52 × 47 = 2444 (m2).
Đáp số: 2444 m2.
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Vì 2 người trong 6 phút sẽ đăng được 6 clip nên sẽ cần 3 nhóm 2 người là 6 người để đăng được 18 clip trong vòng 6 phút.
Do đó ta chọn phương án B.
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải
Đường thẳng y = ax + 5 (d) đi qua M(2; –3) nên ta thay x = 2; y = –3 vào (d) ta được:
2a + 5 = − 3
⇔ 2a = −3 – 5 = −8
⇔ a= −4
Vậy hệ số góc bằng –4.
Câu 36:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Với M(1; 5), thay x = 1 và y = 5 vào y = –5x ta được:
5 = –5.1 Û 5 = –5 (vô lí).
Do đó đồ thị hàm số y = –5x không đi qua điểm M(1; 5).
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
Chiều rộng mảnh đất đó là:
\(36 \times \frac{1}{4} = 9\) (m)
Diện tích mảnh đất đó là:
36 × 9 = 324 (m2)
Đáp số: 324 m2.
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Ta có cos2x + 3sinx – 2 = 0.
⇔ –2sin2x + 3sinx – 1 = 0.
\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x = \frac{1}{2}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\).
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{\pi }{2} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{\pi }{2} < k2\pi < \frac{{39\pi }}{2}\).
\( \Leftrightarrow - \frac{1}{4} < k < \frac{{39}}{4}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (1)
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{\pi }{6} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{\pi }{6} < k2\pi < \frac{{119\pi }}{6}\).
\( \Leftrightarrow - \frac{1}{{12}} < k < \frac{{119}}{{12}}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (2)
⦁ Vì x ∈ (0; 20π) nên \[0 < \frac{{5\pi }}{6} + k2\pi < 20\pi \].
\( \Leftrightarrow - \frac{{5\pi }}{6} < k2\pi < \frac{{115\pi }}{6}\).
\( \Leftrightarrow - \frac{5}{{12}} < k < \frac{{115}}{{12}}\).
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (3)
Từ (1), (2), (3), ta thu được số nghiệm của phương trình đã cho trên khoảng (0; 20π) là 30.
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
Vì x, y ∈ ℤ và (x – 3)(y + 1) = 15 nên ta có bảng sau:
|
x – 3 |
–15 |
–5 |
–3 |
–1 |
1 |
3 |
5 |
15 |
|
y + 1 |
–1 |
–3 |
–5 |
–15 |
15 |
5 |
3 |
1 |
|
x |
–12 |
–2 |
0 |
2 |
4 |
6 |
8 |
18 |
|
y |
–2 |
–4 |
–6 |
–16 |
14 |
4 |
2 |
0 |
|
|
Nhận |
Nhận |
Nhận |
Nhận |
Nhận |
Nhận |
Nhận |
Nhận |
Vậy (x; y) ∈ {(–12; –2), (–2; –4), (0; –6), (2; –16), (4; 14), (6; 4), (8; 2), (18; 0)}.
Câu 40:
 Xem đáp án
Xem đáp án
Lời giải
Điều kiện: x ≥ 2.
Ta có \(M = x + 2\sqrt {x - 2} + 2021 = x - 2 + 2\sqrt {x - 2} + 1 + 2020 = {\left( {\sqrt {x - 2} + 1} \right)^2} + 2020\).
Ta có \(\sqrt {x - 2} \ge 0,\,\forall x \ge 2\).
\( \Leftrightarrow \sqrt {x - 2} + 1 \ge 1,\,\forall x \ge 2\).
\( \Leftrightarrow {\left( {\sqrt {x - 2} + 1} \right)^2} \ge 1,\,\forall x \ge 2\).
\( \Leftrightarrow {\left( {\sqrt {x - 2} + 1} \right)^2} + 2020 \ge 2021,\,\forall x \ge 2\).
Dấu “=” xảy ra ⇔ x = 2.
Vậy Mmin = 2021 khi và chỉ khi x = 2.
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Phương trình hoành độ giao điểm: –x2 – 3x – 1 = x + 3.
⇔ x2 + 4x + 4 = 0.
⇔ (x + 2)2 = 0.
⇔ x = –2.
Với x = –2, ta có y = 1.
Suy ra tọa độ giao điểm A(–2; 1).
Vậy số giao điểm của parabol y = –x2 – 3x – 1 và đường thẳng y = x + 3 là 1.
Câu 42:
Cho \(A = \left( {\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{3 - x}} + \frac{3}{{{x^2} - 4x + 3}}} \right):\frac{5}{{{x^2} - 2x - 3}}\)
a) Rút gọn A.
b) Tính giá trị của A biết 2x2 – x – 1 = 0.
 Xem đáp án
Xem đáp án
Lời giải
a) Với x ≠ ± 1, x ≠ 3 ta có:
\(A = \left( {\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{3 - x}} + \frac{3}{{{x^2} - 4x + 3}}} \right):\frac{5}{{{x^2} - 2x - 3}}\)
\( = \left[ {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x - 3}} + \frac{3}{{\left( {x - 1} \right)\left( {x - 3} \right)}}} \right]:\frac{5}{{\left( {x + 1} \right)\left( {x - 3} \right)}}\)
\( = \frac{{\left( {x + 1} \right)\left( {x - 3} \right) - {{\left( {x - 1} \right)}^2} + 3}}{{\left( {x - 1} \right)\left( {x - 3} \right)}}.\frac{{\left( {x + 1} \right)\left( {x - 3} \right)}}{5}\)
\( = \frac{{{x^2} - 2x - 3 - {x^2} + 2x - 1 + 3}}{{x - 1}}.\frac{{x + 1}}{5}\)
\( = \frac{{ - 1}}{{x - 1}}.\frac{{x + 1}}{5}\)
\( = \frac{{ - x - 1}}{{5\left( {x - 1} \right)}}\).
Vậy với x ≠ ± 1, x ≠ 3 thì \(A = \frac{{ - x - 1}}{{5\left( {x - 1} \right)}}\).
b) Ta có: 2x2 – x – 1 = 0
Û 2x2 – 2x + x – 1 = 0
Û 2x(x – 1) + (x – 1) = 0
Û (x – 1)(2x + 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\2x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\,\left( {ktm} \right)\\x = - \frac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\)
Thay \(x = - \frac{1}{2}\) vào biểu thức A ta được:
\(A = \frac{{\frac{1}{2} - 1}}{{5\left( { - \frac{1}{2} - 1} \right)}} = \frac{{\frac{{ - 1}}{2}}}{{5.\frac{{ - 3}}{2}}} = \frac{{ - 1}}{{ - 15}} = \frac{1}{{15}}\).
Câu 43:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{12}^3.C_9^3.C_6^3.C_3^3\).
Gọi biến cố A: “Nhóm nào cũng có học sinh giỏi và học sinh khá”.
Để nhóm nào cũng có học sinh giỏi và học sinh khá thì:
– Chọn 2 học sinh giỏi và xếp vào 1 trong 4 nhóm thì có \(C_5^2.C_4^1\) cách.
– Xếp 3 học sinh giỏi còn lại vào 3 nhóm còn lại thì có 3! cách.
– Xếp 4 học sinh khá vào 4 nhóm thì có 4! cách.
– Xếp 3 học sinh trung bình thì có 3! cách.
Suy ra \(n\left( A \right) = C_5^2.C_4^1.3!.4!.3!\).
Vì vậy \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_5^2.C_4^1.3!.4!.3!}}{{C_{12}^3.C_9^3.C_6^3.C_3^3}} = \frac{{36}}{{285}}\].
Vậy ta chọn phương án A.
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có \({9^{{x^2} + x - 1}} - {10.3^{{x^2} + x - 2}} + 1 = 0\).
\( \Leftrightarrow {9^{{x^2} + x - 1}} - \frac{{10}}{3}{.3^{{x^2} + x - 1}} + 1 = 0\) (1)
Đặt \(t = {3^{{x^2} + x - 1}}\).
Khi đó phương trình (1) tương đương với: \({t^2} - \frac{{10}}{3}t + 1 = 0\).
\( \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = \frac{1}{3}\end{array} \right.\)
Với t = 3, ta có \({3^{{x^2} + x - 1}} = 3 \Leftrightarrow {x^2} + x - 1 = 1\).
⇔ x2 + x – 2 = 0 ⇔ x = 1 hoặc x = –2.
Với \(t = \frac{1}{3}\), ta có \({3^{{x^2} + x - 1}} = \frac{1}{3} = {3^{ - 1}} \Leftrightarrow {x^2} + x - 1 = - 1\).
⇔ x2 + x = 0 ⇔ x = 0 hoặc x = –1.
Vậy tập nghiệm của phương trình đã cho là: S = {–2; –1; 0; 1}.
Do đó ta chọn phương án C.
Câu 45:
a) Tính giá trị của \(T = C_{2021}^0 + C_{2021}^2 + C_{2021}^4 + ... + C_{2021}^{2020}\).
b) Tính \(S = C_{15}^8 + C_{15}^9 + C_{15}^{10} + ... + C_{15}^{15}\).
 Xem đáp án
Xem đáp án
Lời giải
a) Xét khai triển: \({\left( {1 + x} \right)^{2021}} = C_{2021}^0 + C_{2021}^1.x + ... + C_{2021}^{2020}.{x^{2020}} + C_{2021}^{2021}.{x^{2021}}\).
Thay x = 1 vào khai triển trên, ta được:
\({2^{2021}} = C_{2021}^0 + C_{2021}^1 + ... + C_{2021}^{2020} + C_{2021}^{2021}\) (1)
Thay x = –1 vào khai triển trên, ta được:
\(0 = C_{2021}^0 - C_{2021}^1 + C_{2021}^2 - C_{2021}^3 + ... + C_{2021}^{2020} - C_{2021}^{2021}\).
\( \Leftrightarrow C_{2021}^0 + C_{2021}^2 + ... + C_{2021}^{2020} = C_{2021}^1 + C_{2021}^3 + ... + C_{2021}^{2021}\) (2)
Thế (2) vào (1), ta được:
\(2\left( {C_{2021}^0 + C_{2021}^2 + C_{2021}^4 + ... + C_{2021}^{2020}} \right) = {2^{2021}}\).
Vậy T = 22020.
b) Xét khai triển: \({\left( {1 + x} \right)^{15}} = C_{15}^0 + C_{15}^1.x + ... + C_{15}^{15}.{x^{15}}\).
Thay x = 1 vào khai triển trên, ta được: \({2^{15}} = C_{15}^0 + C_{15}^1 + ... + C_{15}^{15}\).
Mà \(C_{15}^0 = C_{15}^{15};\,\,C_{15}^1 = C_{15}^{14};\,\,C_{15}^2 = C_{15}^{13};\,\,...;\,\,C_{15}^7 = C_{15}^8\).
Khi đó \(2\left( {C_{15}^8 + C_{15}^9 + C_{15}^{10} + ... + C_{15}^{15}} \right) = {2^{15}}\).
Vậy S = 214.
Câu 46:
Tính tổng sau đây:
\(C_{2021}^0 - 2.C_{2021}^1 + {2^2}.C_{2021}^2 - {2^3}.C_{2021}^3 + ... - {2^{2021}}.C_{2021}^{2021}\).
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(C_{2021}^0 - 2.C_{2021}^1 + {2^2}.C_{2021}^2 - {2^3}.C_{2021}^3 + ... - {2^{2021}}.C_{2021}^{2021}\).
\( = C_{2021}^0 + C_{2021}^1.\left( { - 2} \right) + C_{2021}^2.{\left( { - 2} \right)^2} + C_{2021}^3.{\left( { - 2} \right)^3} + ... + C_{2021}^{2021}.{\left( { - 2} \right)^{2021}}\).
\[ = C_{2021}^0{.1^{2021}} + C_{2021}^1{.1^{2020}}.\left( { - 2} \right) + C_{2021}^2{.1^{2019}}.{\left( { - 2} \right)^2} + C_{2021}^3{.1^{2018}}.{\left( { - 2} \right)^3} + ... + C_{2021}^{2021}.{\left( { - 2} \right)^{2021}}\].
= [(1 + (–2)]2021 = (–1)2021 = –1.
Vậy \(C_{2021}^0 - 2.C_{2021}^1 + {2^2}.C_{2021}^2 - {2^3}.C_{2021}^3 + ... - {2^{2021}}.C_{2021}^{2021} = - 1\).
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: Số lớn – Số bé + Hiệu = 2 × Hiệu = 12.
Hiệu số phần bằng nhau là: 11 – 9 = 2 (phần).
Hiệu của hai số đó là: 12 : 2 = 6.
Số lớn là: 6 : 2 × 11 = 33.
Vì 33 > 30 nên A > 30.
Vậy A > 30.
Câu 48:
Cho a, b, c là độ dài 3 cạnh của một tam giác. Chứng minh rằng:
\(\frac{1}{{a + b - c}} + \frac{1}{{b + c - a}} + \frac{1}{{c + a - b}} \ge \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\).
 Xem đáp án
Xem đáp án
Lời giải
Do a, b, c là độ dài 3 cạnh của một tam giác nên \(\left\{ \begin{array}{l}a + b - c > 0\\b + c - a > 0\\c + a - b > 0\end{array} \right.\).
Áp dụng bất đẳng thức Cauchy, ta được:
⦁ \(\frac{1}{{a + b - c}} + \frac{1}{{b + c - a}} \ge \frac{4}{{2b}} = \frac{2}{b}\);
⦁ \(\frac{1}{{a + b - c}} + \frac{1}{{c + a - b}} \ge \frac{4}{{2a}} = \frac{2}{a}\);
⦁ \(\frac{1}{{b + c - a}} + \frac{1}{{c + a - b}} \ge \frac{4}{{2c}} = \frac{2}{c}\).
Cộng vế theo vế ba bất đẳng thức trên, ta được:
\(2.\left( {\frac{1}{{a + b - c}} + \frac{1}{{b + c - a}} + \frac{1}{{c + a - b}}} \right) \ge \frac{2}{a} + \frac{2}{b} + \frac{2}{c} = 2.\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)\).
\( \Leftrightarrow \frac{1}{{a + b - c}} + \frac{1}{{b + c - a}} + \frac{1}{{c + a - b}} \ge \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\).
Dấu “=” xảy ra ⇔ a = b = c.
Vậy ta có điều phải chứng minh.
Câu 49:
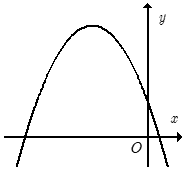
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ bên.
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Bề lõm của đồ thị hướng xuống nên a < 0.
Hoành độ đỉnh parabol \(x = \frac{{ - b}}{{2a}} < 0\).
Mà a < 0.
Suy ra –b > 0.
Do đó b < 0.
Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.
Vậy a < 0, b < 0, c > 0.
Do đó ta chọn phương án D.
Câu 50:
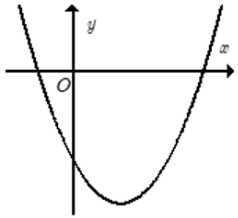
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Bề lõm của đồ thị hướng lên nên a > 0.
Hoành độ đỉnh parabol \(x = \frac{{ - b}}{{2a}} > 0\).
Mà a > 0.
Suy ra –b > 0.
Do đó b < 0.
Parabol cắt trục tung tại điểm có tung độ âm nên c < 0.
Vậy a > 0, b < 0, c < 0.
Do đó ta chọn phương án A.
Câu 51:
 Xem đáp án
Xem đáp án
Lời giải
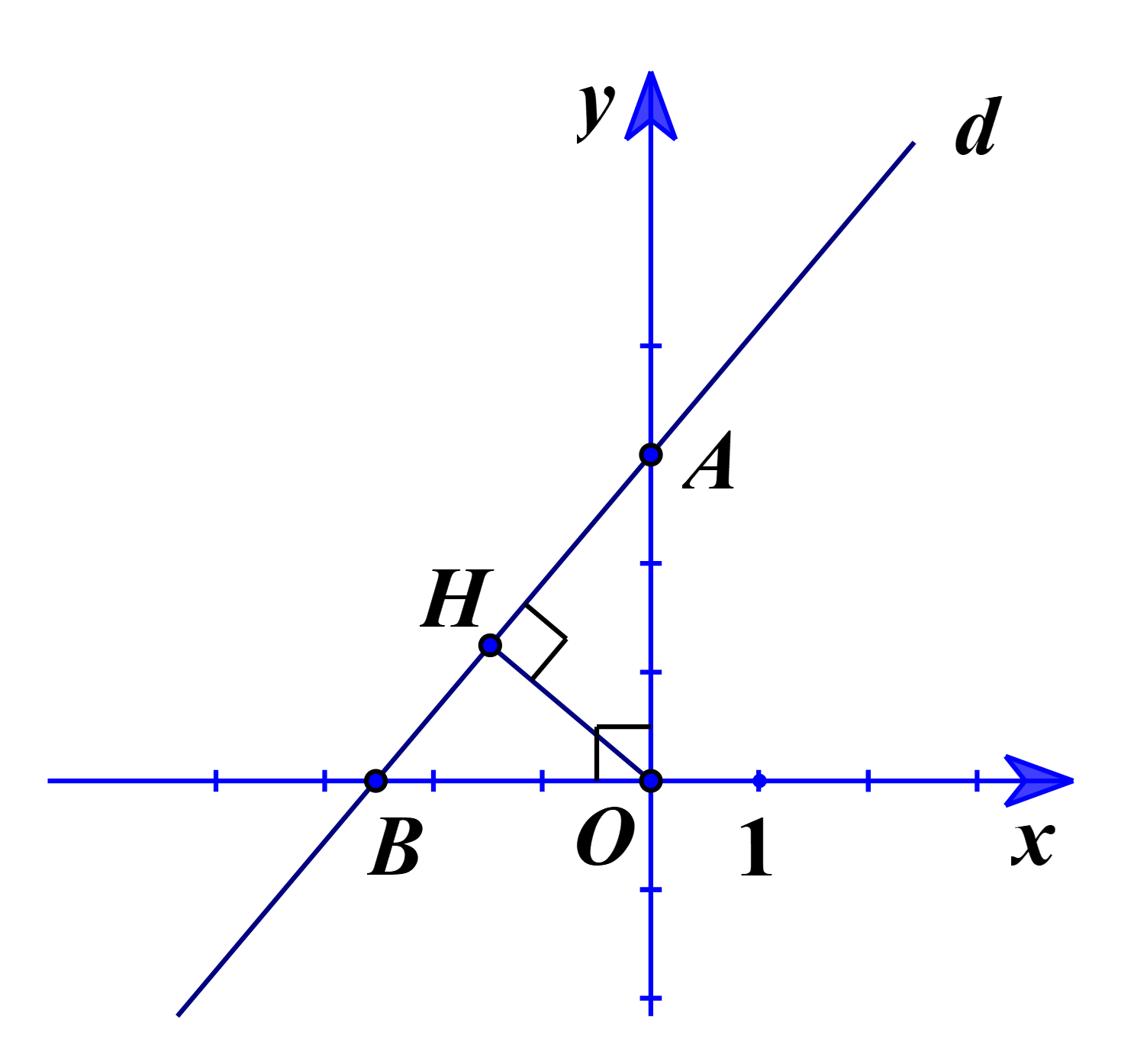
Gọi A, B lần lượt là giao điểm của đường thẳng d với các trục Oy, Ox.
Với x = 0, ta có: y = 3. Suy ra tọa độ A(0; 3).
Với y = 0, ta có: \(x = \frac{{ - 3}}{m}\). Suy ra tọa độ \(B\left( {\frac{{ - 3}}{m};0} \right)\).
Kẻ OH vuông góc với AB.
Khi đó khoảng cách từ gốc tọa độ O đến đường thẳng d là lớn nhất.
⇔ OH lớn nhất.
⇔ OH2 lớn nhất.
Ta có OA = |3| = 3, \[OB = \left| {\frac{{ - 3}}{m}} \right| = \frac{3}{{\left| m \right|}}\].
Tam giác OAB vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{9} + \frac{{{m^2}}}{9} = \frac{{{m^2} + 1}}{9}\).
Suy ra \(O{H^2} = \frac{9}{{{m^2} + 1}}\).
Ta có m2 ≥ 0, ∀m.
⇔ m2 + 1 ≥ 1, ∀m.
\( \Leftrightarrow \frac{9}{{{m^2} + 1}} \le 9,\,\forall m\).
Dấu “=” xảy ra ⇔ m = 0.
Vậy m = 0 thỏa mãn yêu cầu bài toán.
Câu 52:
 Xem đáp án
Xem đáp án
Lời giải
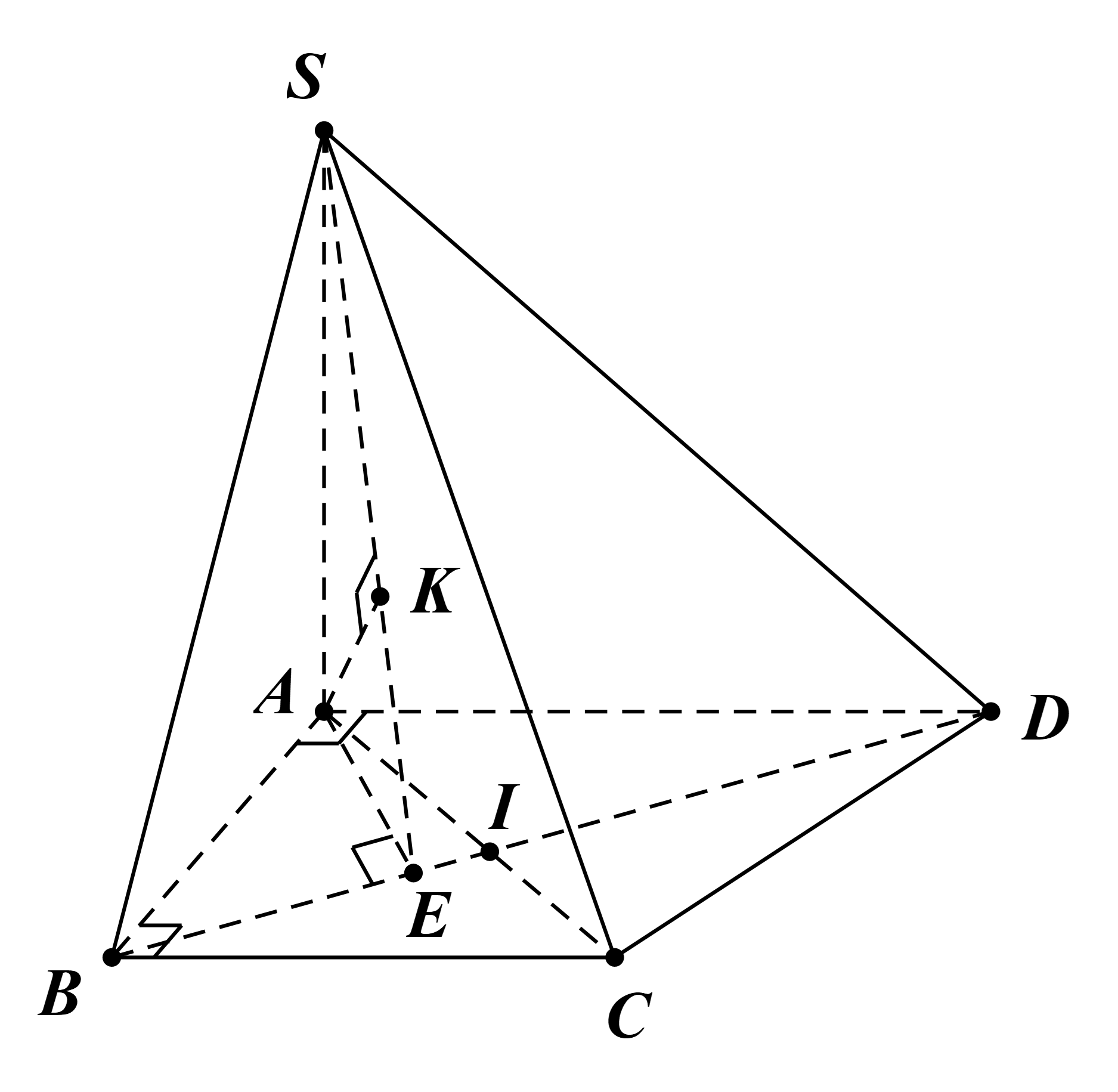
Trong (ABCD): kẻ AE ⊥ BD.
Trong (SAE): kẻ AK ⊥ SE.
Ta có BD ⊥ AE và BD ⊥ SA.
Suy ra BD ⊥ (SAE).
Do đó BD ⊥ AK.
Mà AK ⊥ SE.
Vì vậy AK ⊥ (SBD).
Khi đó d(A, (SBD)) = AK.
Tam giác ABD vuông tại A có AE là đường cao:
\(AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{a.a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}\).
Tam giác SAE vuông tại A có AK là đường cao:
\(AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \frac{{a\sqrt 2 .\frac{{a\sqrt 6 }}{3}}}{{\sqrt {2{a^2} + \frac{{2{a^2}}}{3}} }} = \frac{{a\sqrt 2 }}{2}\).
Do đó \(d\left( {A,\left( {SBD} \right)} \right) = AK = \frac{{a\sqrt 2 }}{2}\).
Trong (ABCD): gọi I = AC ∩ BD.
Ta có AB = BC = a và \(\widehat {ABC} = 90^\circ \).
Suy ra tam giác ABC vuông cân tại B.
Do đó \(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \) và \(\widehat {BAC} = \widehat {BCA} = 45^\circ \).
Mà \(\widehat {IAD} = \widehat {BAD} - \widehat {BAC} = 45^\circ \).
Suy ra AI là tia phân giác của \(\widehat {BAD}\).
Áp dụng tính chất đường phân giác, ta có: \(\frac{{IB}}{{ID}} = \frac{{AB}}{{AD}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\).
Do đó \(ID = \sqrt 2 IB\).
Ta có \(IB + ID = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 3 \).
\( \Rightarrow IB + \sqrt 2 IB = a\sqrt 3 \).
\( \Rightarrow IB = \frac{{a\sqrt 3 }}{{1 + \sqrt 2 }} = a\left( {\sqrt 6 - \sqrt 3 } \right)\).
Ta có \(I{B^2} = A{B^2} + A{I^2} - 2AB.AI.\cos \widehat {BAI}\).
\[ \Rightarrow A{I^2} - a\sqrt 2 .AI + \left( {6\sqrt 2 - 8} \right){a^2} = 0\].
\( \Rightarrow \left[ \begin{array}{l}AI = a\left( {2\sqrt 2 - 2} \right)\\AI = a\left( {2 - \sqrt 2 } \right)\end{array} \right.\)
Vì AI > IB nên ta nhận \(AI = a\left( {2\sqrt 2 - 2} \right)\).
Với \(AI = a\left( {2\sqrt 2 - 2} \right)\), ta có \(IC = AC - AI = a\left( {2 - \sqrt 2 } \right)\).
Khi đó \(d\left( {C,\left( {SBD} \right)} \right) = \frac{{IC}}{{IA}}.d\left( {A,\left( {SBD} \right)} \right) = \frac{{a\left( {2 - \sqrt 2 } \right)}}{{a\left( {2\sqrt 2 - 2} \right)}}.\frac{{a\sqrt 2 }}{2} = \frac{a}{2}\).
Vậy khoảng cách h từ C đến mặt phẳng (SBD) bằng \(\frac{a}{2}\).
