Giải bởi Vietjack
Lời giải
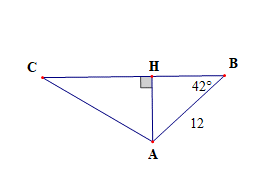
Kẻ AH ⊥ BC
Xét tam giác ABH có
AH = AB . sinB = 12 . sin42° ≈ 8 (cm)
Áp dụng định lý Pytago trong tam giác AHB vuông tại H có
BH2 = AB2 – AH2 = 122 – 82 = 80
Suy ra \(BH = 4\sqrt 5 \) (cm)
Khi đó \(CH = BC - BH = 22 - 4\sqrt 5 \)
Áp dụng định lý Pytago trong tam giác AHC vuông tại H có
AC2 = AH2 + CH2
Suy ra \[{\rm{A}}C = \sqrt {{8^2} + {{\left( {22 - 4\sqrt 5 } \right)}^2}} \approx 15,3\] (cm)
Mà \[\sin C = \frac{{AH}}{{AC}} = \frac{8}{{15,3}}\]
Suy ra \(\widehat C \approx 31^\circ \)
Xét tam giác ABC có
\(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {BAC} + 42^\circ + 31^\circ = 180^\circ \)
Suy ra \(\widehat {BAC} = 107^\circ \)
Vậy \(\widehat {BAC} = 107^\circ ;\widehat C = 31^\circ ;AC = 15,3cm.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB kẻ hai tia Ax, By vuông góc với AB. Trên tia Ax và By lần lượt lấy hai điểm C và D sao cho \(\widehat {CO{\rm{D}}} = 90^\circ \) (O là trung điểm của AB). Chứng minh rằng:
a) CD = AC + BD
b) CD là tiếp tuyến của đường tròn đường kính AB
c) \(AC.B{\rm{D}} = \frac{{A{B^2}}}{4}\).
Tính nhanh:
\[{\rm{A}} = \left( {\frac{1}{4} - 1} \right).\left( {\frac{1}{9} - 1} \right).\left( {\frac{1}{{16}} - 1} \right).\left( {\frac{1}{{25}} - 1} \right).....\left( {\frac{1}{{121}} - 1} \right).\]
Cho hàm số y = (m – 2)x + 2m + 1 (m là tham số)
a) Với giá trị nào của m thì hàm số đồng biến?
b) Tìm m để đồ thị hàm số song song đường thẳng y = 2x – 1.
c) Tìm điểm cố định mà đồ thị hàm số luôn luôn đi qua với mọi giá trị m.
Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d’)
a) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ.
b) Hai đường thẳng (d) và (d’) cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ các điểm A, B, C.
c) Tính chu vi và diện tích của tam giác ABC.
d) Tính góc tạo bởi đường thẳng y = x + 1 với trục Ox.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu H trên AB, AC. Chứng minh:
a) \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\);
b) BC2 = 3AH2 + BE2 + CF2;
c) \(BE\sqrt {CH} + CF\sqrt {BH} = AH\sqrt {BC} \).
Cho tam giác ABC cân tại A có đường cao AH, kẻ BK vuông góc AC. Chứng minh:
\(\frac{1}{{B{K^2}}} = \frac{1}{{4B{C^2}}} + \frac{1}{{4A{H^2}}}\).
