Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 35)
-
2065 lượt thi
-
48 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:
a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?
 Xem đáp án
Xem đáp án
Lời giải
a) Chị Hoa phải trả số tiền là:
1 050 000 – 1 050 000 × 30% = 735 000 (đồng)
b) Giá chiếc túi đã giảm khi có thẻ khách hàng thân thiết là:
91 000 : 10% = 910 000 (đồng)
Giá chiếc túi ban đầu là:
910 000 : (1 – 30%) = 1 300 000 (đồng)
Vậy giá niêm yết ban đầu của túi xách là 1 300 000 đồng.
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Áp dụng công thức Heron cho tam giác ABC, ta có:
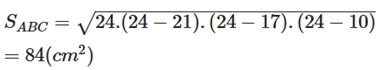
Suy ra:
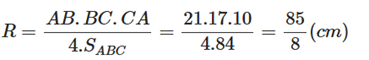
Vậy ta chọn đáp án C.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
3x2 + 6y2 + 2z2 + 3y2z2 – 18x = 6
⇔ (3x2 – 18x + 27) + 6y2 + 2z2 + 3y2z2 = 6 + 27
⇔ 3(x – 3)2 + 6y2 + 2z2 + 3y2z2 = 33 (1)
Vì x, y, z nguyên nên z2 ⋮ 3 và 2z2 ≤ 33
Hay |z| ≤ 3
Mà z nguyên
Suy ra z = 0 hoặc z = 3
+) TH1: z = 0
(1) ⇔ 3(x – 3)2 + 6y2 = 33
⇔ (x – 3)2 + 2y2 = 11
Suy ra 2y2 ≤ 11
Do đó |y| ≤ 2
\( \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = 1\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{\left( {x - 3} \right)^2} = 11\\{\left( {x - 3} \right)^2} + 2 = 11\end{array} \right.\)
⇔ (x – 3)2 + 2 = 11 (vì x nguyên)
⇔ (x – 3)2 = 9 \( \Leftrightarrow \left[ \begin{array}{l}x - 3 = 3\\x - 3 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\\x = 0\end{array} \right.\)
+) TH1: z = 3
(1) ⇔ 3(x – 3)2 + 6y2 + 2 . 32 + 3y2 . 32 = 33
⇔ 3(x – 3)2 + 33y2 + 18 = 33
⇔ (x – 3)2 + 11y2 = 5
Suy ra 11y2 ≤ 5
Do đó y = 0
Khi đó (x – 3)2 = 5 nên không tìm được giá trị x nguyên thỏa mãn phương trình
Vậy phương trình đã cho có nghiệm nguyên (x, y, z) là: (0; 1; 0), (0; –1; 0), (6; 1; 0), (6; –1; 0).
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu H trên AB, AC. Chứng minh:
a) \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\);
b) BC2 = 3AH2 + BE2 + CF2;
c) \(BE\sqrt {CH} + CF\sqrt {BH} = AH\sqrt {BC} \).
 Xem đáp án
Xem đáp án
Lời giải
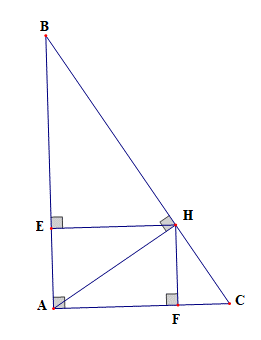
a) Xét tam giác ABC vuông tại A có AH ⊥ BC, theo hệ thức lượng trong tam giác vuông ta có:
AB2 = BH . BC
AC2 = CH . BC
Xét tam giác ABH vuông tại H có HE ⊥ AB, theo hệ thức lượng trong tam giác vuông ta có:
BH2 = BE . BA
Hay \(BE = \frac{{B{H^2}}}{{BA}}\)
Xét tam giác ACH vuông tại H có HF ⊥ AC, theo hệ thức lượng trong tam giác vuông ta có:
CH2 = CF . CA
Hay \(CF = \frac{{C{H^2}}}{{CA}}\)
Ta có: \(\frac{{A{B^4}}}{{A{C^4}}} = \left( {\frac{{A{B^2}}}{{A{C^2}}}} \right) = \frac{{{{\left( {BH.BC} \right)}^2}}}{{{{\left( {CH.BC} \right)}^2}}} = \frac{{B{H^2}}}{{C{H^2}}} = \frac{{BE.AB}}{{CF.AC}} = \frac{{BE}}{{CF}}.\frac{{AB}}{{AC}}\)
Suy ra \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\)
Vậy \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\).
b) Xét tứ giác AEHF có \(\widehat {{\rm{EAF}}} = \widehat {HE{\rm{A}}} = \widehat {HF{\rm{A}}} = 90^\circ \)
Suy ra AEHF là hình chữ nhật
Do đó AH = EF
Xét tam giác ABC vuông tại A , theo định lý Pytago ta có:

Vậy BC2 = 3AH2 + BE2 + CF2
c) Ta có: \(BE\sqrt {CH} + CF\sqrt {BH} \)
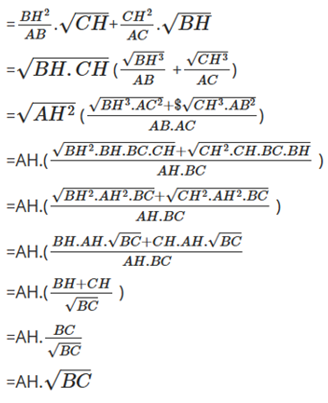
Vậy \(BE\sqrt {CH} + CF\sqrt {BH} = AH\sqrt {BC} \).
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\(27{{\rm{x}}^3} + \frac{{{y^3}}}{8} = {\left( {3{\rm{x}}} \right)^3} + {\left( {\frac{y}{2}} \right)^3}\)
\( = \left( {3{\rm{x}} + \frac{y}{2}} \right)\left[ {{{\left( {3{\rm{x}}} \right)}^2} - 3{\rm{x}}.\frac{y}{2} + {{\left( {\frac{y}{2}} \right)}^2}} \right]\)
\( = \left( {3{\rm{x}} + \frac{y}{2}} \right)\left( {9{{\rm{x}}^2} + \frac{3}{2}xy + \frac{1}{4}{y^2}} \right)\)
Câu 6:
Tính nhanh:
\[{\rm{A}} = \left( {\frac{1}{4} - 1} \right).\left( {\frac{1}{9} - 1} \right).\left( {\frac{1}{{16}} - 1} \right).\left( {\frac{1}{{25}} - 1} \right).....\left( {\frac{1}{{121}} - 1} \right).\]
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\[{\rm{A}} = \left( {\frac{1}{4} - 1} \right).\left( {\frac{1}{9} - 1} \right).\left( {\frac{1}{{16}} - 1} \right).\left( {\frac{1}{{25}} - 1} \right).....\left( {\frac{1}{{121}} - 1} \right)\]
\[{\rm{A}} = \left( { - \frac{3}{4}} \right).\left( { - \frac{8}{9}} \right).\left( { - \frac{{15}}{{16}}} \right).....\left( { - \frac{{120}}{{121}}} \right)\] (có 10 số hạng)
\[{\rm{A}} = \frac{{3.8.15.....120}}{{4.9.16.....121}}\]
\[{\rm{A}} = \frac{{\left( {1.3} \right).\left( {2.4} \right).\left( {3.5} \right).....\left( {10.12} \right)}}{{{2^2}{{.3}^2}{{.4}^2}{{.....11}^2}}}\]
\[{\rm{A}} = \frac{{\left( {1.2.3.....10} \right).\left( {3.4.5.....12} \right)}}{{\left( {2.3.4.....11} \right).\left( {2.3.4.....11} \right)}}\]
\(A = \frac{{12}}{{11.2}} = \frac{6}{{11}}\).
Câu 7:
Cho A = (5; 7] và B = [m; m + 3). Tìm m để:
a) A tập hợp con của B.
b) B tập hợp con của A.
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có: \[{\rm{A}} \subset B \Leftrightarrow \left\{ \begin{array}{l}m \le 5\\m + 3 > 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 5\\m > 4\end{array} \right. \Leftrightarrow 4 < m \le 5\].
b) Ta có: \[B \subset A \Leftrightarrow \left\{ \begin{array}{l}m > 5\\m + 3 \le 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 5\\m \le 4\end{array} \right. \Leftrightarrow m \in \emptyset \].
Câu 8:
Cho A = (2m – 1; m + 3) và B = (–4; 5). Tìm m sao cho
a) A là tập hợp con của B.
b) B là tập hợp con của A.
c) A ∩ B = ∅.
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có:
\[{\rm{A}} \subset B \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \ge - 4\\m + 3 \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m \ge - 3\\m \le 2\end{array} \right. \Leftrightarrow \frac{{ - 3}}{2} \le m \le 2\].
b) Ta có:
\[B \subset A \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \le - 4\\m + 3 \ge 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m \le - 3\\m \ge 2\end{array} \right. \Leftrightarrow m \in \emptyset \].
c) Ta có:
\(A \cap B = \emptyset \Leftrightarrow \left[ \begin{array}{l}m + 3 < 4\\2m - 1 > 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 3\end{array} \right.\).
Câu 9:
Tìm x biết:
a) (2x + 3)(x – 4) + (x – 5)(x – 2) = (3x – 5)(x – 4).
b) (8x – 3)(3x + 2) – (4x + 7)(x + 4) = (2x + 1)(5x – 1).
 Xem đáp án
Xem đáp án
Lời giải
a) (2x + 3)(x – 4) + (x – 5)(x – 2) = (3x – 5)(x – 4)
⇔ 2x2 – 8x + 3x – 12 + x2 – 2x – 5x + 10 = 3x2 – 12x – 5x + 20
⇔ –12x – 2 = – 17x + 20
⇔ 5x = 22
\( \Leftrightarrow x = \frac{{22}}{5}\)
Vậy \(x = \frac{{22}}{5}\).
b) (8x – 3)(3x + 2) – (4x + 7)(x + 4) = (2x + 1)(5x – 1)
⇔ 24x2 – 9x + 16x – 6 – 4x2 – 16x – 7x – 28 = 10x2 – 2x + 5x – 1
⇔ 20x2 – 16x – 34 = 10x2 + 3x – 1
⇔ 10x2 – 19x – 33 = 0
⇔ 10x2 – 30x + 11x – 33 = 0
⇔ 10x(x – 3) + 11(x – 3) = 0
⇔ (10x + 11)(x – 3) = 0
\( \Leftrightarrow \left[ \begin{array}{l}10{\rm{x}} + 11 = 0\\x - 3 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{{ - 11}}{{10}}\\x = 3\end{array} \right.\)
Vậy \(x = \frac{{ - 11}}{{10}}\) hoặc x = 3.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
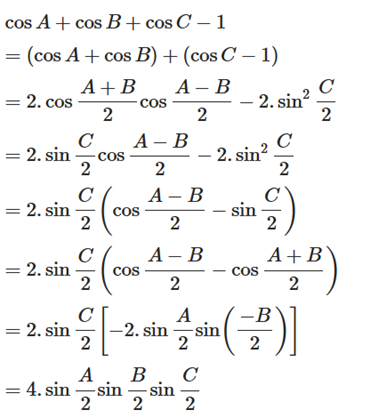
Suy ra \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\]
Vậy \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\].
Câu 11:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có: \(y = \sin \left( {\frac{2}{5}x} \right).c{\rm{os}}\left( {\frac{2}{5}x} \right) = \frac{1}{2}\sin \left( {\frac{4}{5}x} \right)\)
Do đó f là hàm số tuấn hoàn với chu kì \(T = \frac{{2\pi }}{{\frac{4}{5}}} = \frac{{5\pi }}{2}\)
Vậy ta chọn đáp án C.
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Hàm số xác định trên R

Mà m nguyên
Suy ra m ∈ {–4; –3; –2; –1; 0; 1; 2; 3}
Do đó có 8 giá trị của m.
Vậy ta chọn đáp án B.Câu 13:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
VT = (–a – b)2 = [– (a + b)2] = (a + b)2 = VP
Vậy (–a – b)2 = (a + b)2.
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
27x3 – 27x2 + 9x – 1 = 0
⇔ (3x)3 – 3(3x)2 . 1 + 3 . 3x . 11 – 13 = 0
⇔ (3x – 1)3 = 0
⇔ 3x – 1 = 0
\( \Leftrightarrow x = \frac{1}{3}\)
Vậy \(x = \frac{1}{3}\).
Câu 15:
Cho tam giác ABC có các góc thỏa mãn: \(2c{\rm{osA + cosB + cosC = }}\frac{9}{4}\).
Tính \(\sin \frac{A}{2}\).
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\(2c{\rm{osA + cosB + cosC = }}\frac{9}{4}\)
\( \Leftrightarrow 2c{\rm{osA + 2cos}}\left( {\frac{{{\rm{B + C}}}}{2}} \right){\rm{cos}}\left( {\frac{{B - C}}{2}} \right){\rm{ = }}\frac{9}{4}\)
\( \Leftrightarrow c{\rm{osA + cos}}\left( {\frac{{{\rm{B + C}}}}{2}} \right){\rm{cos}}\left( {\frac{{B - C}}{2}} \right){\rm{ = }}\frac{9}{8}\)
\( \Leftrightarrow c{\rm{osA + sin}}\frac{A}{2}{\rm{cos}}\left( {\frac{{B - C}}{2}} \right){\rm{ = }}\frac{9}{8}\)
\( \Leftrightarrow 1 - 2{\sin ^2}\frac{A}{2}{\rm{ + }}\sin A{\rm{cos}}\left( {\frac{{B - C}}{2}} \right){\rm{ = }}\frac{9}{8}\)
\( \Leftrightarrow - 2{\sin ^2}\frac{A}{2}{\rm{ + }}\sin \frac{A}{2}{\rm{cos}}\left( {\frac{{B - C}}{2}} \right) - \frac{1}{8}{\rm{ = 0}}\) (1)
Để tồn tại góc A thì phương trình (1) phải có nghiệm \(\sin \frac{A}{2}\)
Suy ra ∆ ≥ 0
\( \Leftrightarrow co{s^2}\left( {\frac{{B - C}}{2}} \right) - 1 \ge 0\)
\( \Leftrightarrow cos\left( {\frac{{B - C}}{2}} \right) = 1\)
Khi đó \( - 2{\sin ^2}\frac{A}{2}{\rm{ + }}\sin \frac{A}{2} - \frac{1}{8}{\rm{ = 0}}\)
\( \Leftrightarrow {\sin ^2}\frac{A}{2}{\rm{ }} - \frac{1}{2}\sin \frac{A}{2} + \frac{1}{{16}}{\rm{ = 0}}\)
\( \Leftrightarrow {\left( {\sin \frac{A}{2} - \frac{1}{4}} \right)^2}{\rm{ = 0}}\)
\( \Leftrightarrow \sin \frac{A}{2} = \frac{1}{4}\)
Vậy \(\sin \frac{A}{2} = \frac{1}{4}\).
Câu 16:
Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d’)
a) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ.
b) Hai đường thẳng (d) và (d’) cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ các điểm A, B, C.
c) Tính chu vi và diện tích của tam giác ABC.
d) Tính góc tạo bởi đường thẳng y = x + 1 với trục Ox.
 Xem đáp án
Xem đáp án
Lời giải
a) Hàm số: y = x + 1
Cho x = 0 thì y = 0 + 1 = 1, ta có điểm M(0; 1)
Cho y = 0 thì 0 = x + 1 nên x = –1, ta có điểm P(–1; 0)
Đồ thị hàm số y = x + 1 là đường thẳng đi qua hai điểm M(0; 1) và P(–1; 0)
+) Hàm số: y = –x + 3
Cho x = 0 thì y = 0 + 3 = 3, ta có điểm N(0; 3)
Cho y = 0 thì 0 = –x + 3 nên x = 3, ta có điểm Q(3; 0)
Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm N(0; 3) và Q(3; 0)
Ta có hình vẽ sau:
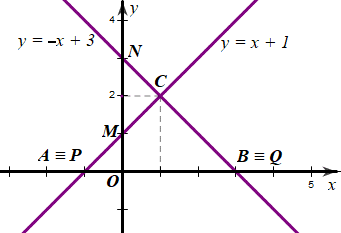
b) Hoành độ của điểm C là nghiệm của phương trình
x + 1 = –x + 3
⇔ 2x = 2
⇔ x = 1
Suy ra y = 1 + 1 = 2
Vậy C(1; 2)
Hoành độ của điểm A là nghiệm của phương trình
x + 1 = 0 ⇔ x = –1
Suy ra A(–1; 0) ≡ P
Hoành độ của điểm B là nghiệm của phương trình
–x + 3 = 0 ⇔ x = 3
Suy ra B(3; 0) ≡ Q
c) Ta có AB = OA + OB = 1 + 3 = 4
Áp dụng định lý Pytago ta có
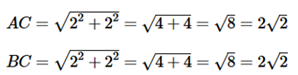
Chu vi tam giác ABC là:
![]()
Ta có:
![]()
Suy ra tam giác ABC vuông tại C
Diện tích tam giác ABC là
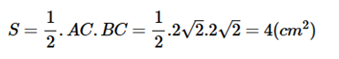
d) Xét tam giác ABC có
\(\sin {\rm{A}} = \frac{{BC}}{{AB}} = \frac{{2\sqrt 2 }}{4} = \frac{{\sqrt 2 }}{2}\)
Suy ra \(\widehat A = 45^\circ \)
Vậy góc tạo bởi đường thẳng y = x + 1 với trục Ox bằng 45°.
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải
Tổng 2 số là:
9 × 2 = 18
Số kia là:
18 – 12 = 6
Vậy số còn lại là 6.
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
A ∪ B = (–∞; +∞)
Suy ra (A ∪ B ) ∩ C = (0; 1)
Vậy (A ∪ B ) ∩ C = (0; 1).
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\[b \subset a \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m + 3 \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \le - 1\end{array} \right. \Leftrightarrow m \le - 1\].
Vậy m < –1 thì b ⊂ a.
Câu 20:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
3c2 = c(a + b) + ab
⇔ 2c2 = ca + cb + ab + c2
⇔ 2c2 = c(a + c) + b(c + a)
⇔ 2c2 = (a + c) (b + c)
Gọi d gcd(a + c, b + c)
Do a – b = p ∈ P nên d = 1 hoặc d = p
+) Nếu d = 1
Thì a + c = x2, b + c = y2 (xy = 2c)
Suy ra p = (x – y)(x + y).p = 2 (vô lý)
p lẻ thì dễ thấy \[{\rm{x}} = \frac{{p + 1}}{2} = \frac{{a - b + 1}}{2}\] và \(y = \frac{{a - b - 1}}{2}\)
Suy ra \(2c = xy = \frac{{\left( {a - b - 1} \right)\left( {a - b + 1} \right)}}{4}\)
Do đó 8c + 1 = (a – b)2 là số chính phương
+) Nếu d = p thì a + c = pm2, b + c = pn2 (2c = pmn)
Suy ra (m – n)(m + n) = 1
Do đó m = 1 và n = 0 (loại)
Vậy 8c + 1 là số chính phương.
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
Hàng trăm có 3 lựa chọn
Hàng chục có 3 lựa chọn
Hàng đơn vị có 3 lựa chọn
Ta lập được tất cả số tự nhiên có 3 chữ số là:
3 × 3 × 3 = 27 (số)
Vậy lập được 27 số có 3 chữ số.
Câu 22:
Cho biết tổng của sáu số là 42, hãy tính trung bình cộng của sáu số đó.
 Xem đáp án
Xem đáp án
Lời giải
Trung bình cộng của 6 số đó là:
42 : 6 = 7
Vậy trung bình cộng của 6 số đó là 7.
Câu 23:
Cho hàm số y = (m – 2)x + 2m + 1 (m là tham số)
a) Với giá trị nào của m thì hàm số đồng biến?
b) Tìm m để đồ thị hàm số song song đường thẳng y = 2x – 1.
c) Tìm điểm cố định mà đồ thị hàm số luôn luôn đi qua với mọi giá trị m.
 Xem đáp án
Xem đáp án
Lời giải
a) Để hàm số y = (m – 2)x + 2m + 1 đồng biến
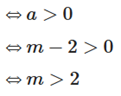
Vậy với m > 2 thì hàm số y = (m – 2)x + 2m + 1 đồng biến.
b) Để đồ thị hàm số y = (m – 2)x + 2m + 1 song song đường thẳng y = 2x – 1
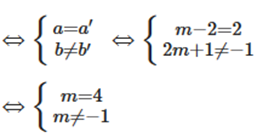
Vậy m = 4 và m ≠ 1.
c) Giả sử đồ thị hàm số y = (m – 2)x + 2m + 1 luôn đi qua một điểm cố định M(x0; y0) với mọi m
Khi đó y0 = (m – 2)x0 + 2m + 1
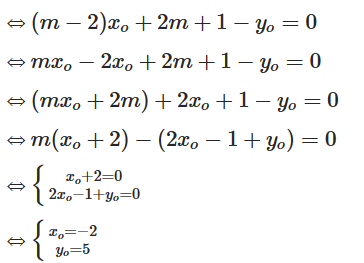
Vậy điểm cố định mà đồ thị hàm số luôn luôn đi qua với mọi giá trị m là M(–2; 5).
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
c4 – 2(a2 + b2)c2 + a4 + a2b2 + b4 = 0
⇔ c4 – 2(a2 + b2)c2 + (a4 + 2a2b2 + b4) – a2b2 = 0
⇔ c4 – 2(a2 + b2)c2 + (a2 + b2)2 – a2b2 = 0
⇔ (a2 + b2 – c2)2 – a2b2 = 0
⇔ (a2 + b2 – c2 – ab)(a2 + b2 – c2 + ab) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{a^2} + {b^2} - {c^2} - ab = 0\\{a^2} + {b^2} - {c^2} + ab = 0\end{array} \right.\)
Áp dụng định lý cosin:
Nếu a2 + b2 – c2 – ab = 0 hay a2 + b2 – c2 = ab
\[{\rm{cosC}} = \frac{{{a^2} + {b^2} - {c^2}}}{{2{\rm{a}}b}} = \frac{{ab}}{{2{\rm{a}}b}} = \frac{1}{2}\]
Suy ra \(\widehat C = 60^\circ \)
Nếu a2 + b2 – c2 + ab = 0 hay a2 + b2 – c2 = –ab
\[{\rm{cosC}} = \frac{{{a^2} + {b^2} - {c^2}}}{{2{\rm{a}}b}} = \frac{{ - ab}}{{2{\rm{a}}b}} = \frac{{ - 1}}{2}\]
Suy ra \(\widehat C = 120^\circ \).
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
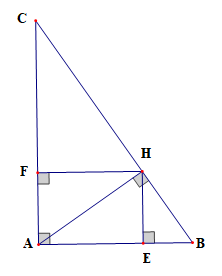
Xét tam giác ABH vuông ở H có HE ⊥ AB, theo hệ thức lượng trong tam giác vuông ta có HB2 = BE . AB
Suy ra \(BE = \frac{{H{B^2}}}{{AB}}\)
Xét tam giác ACH vuông ở H có HF ⊥ AC, heo hệ thức lượng trong tam giác vuông ta có
HC2 = CF . AC
Suy ra \(CF = \frac{{H{C^2}}}{{AC}}\)
Xét tam giác ACB vuông ở A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông ta có
AC2 = CH . BC
AB2 = BH . BC
Suy ra
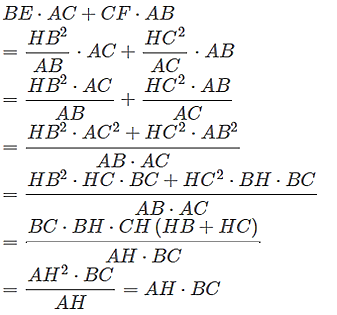
Vậy BE . AC + CF . AB = AH . BC.
Câu 26:
Cho tam giác ABC vuông tại A và đường cao AH. Biết \(\widehat A = 90^\circ \), AB = 15 cm, AC = 20 cm.
a) Tính cạnh BC.
b) Tính độ dài của AH, BH và HC.
 Xem đáp án
Xem đáp án
Lời giải
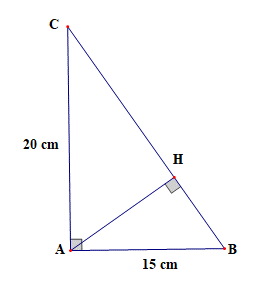
a) Vì tam giác ABC vuông tại A
Nên BC2 = AB2 + AC2
Hay BC2 = 152 + 202 = 625
Suy ra BC = 25 (cm)
b) Xét tam giác ACB vuông ở A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông ta có
AC2 = CH . BC nên \(CH = \frac{{A{C^2}}}{{BC}} = \frac{{{{20}^2}}}{{25}} = 16\)
AB2 = BH . BC nên \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{{15}^2}}}{{25}} = 9\)
AH2 = BH . CH = 16 . 9 = 144
Suy ra AH = 12 (cm)
Vậy AH = 12 cm, BH = 9 cm, CH = 16 cm.
Câu 27:
Cho tứ giác ABCD nội tiếp (O). Gọi E là giao điểm của AB, CD. F là giao điểm của AC và BD. Đường tròn ngoại tiếp tam giác BDE cắt đường tròn ngoại tiếp tam giác FDC tại điểm K khác D. Tiếp tuyến của (O) tại B và C cắt nhau tại M.
a) Chứng minh tứ giác BKCM nội tiếp.
b) Chứng minh E, M, F thẳng hàng.
 Xem đáp án
Xem đáp án
Lời giải
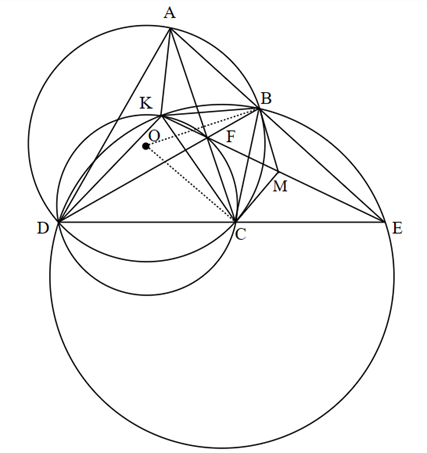
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn
Suy ra \(\widehat {BEK} = \widehat {B{\rm{D}}K}\) (2 góc nội tiếp cùng chắn cung BK)
Hay \(\widehat {AEK} = \widehat {{\rm{FD}}K}\)
Vì tứ giác DKFC nội tiếp đường tròn nên \(\widehat {FCK} = \widehat {{\rm{FD}}K}\)
Suy ra \(\widehat {AEK} = \widehat {{\rm{FC}}K}\), hay \(\widehat {AEK} = \widehat {{\rm{AC}}K}\)
Do đó tứ giác AKCE nội tiếp đường tròn
Suy ra \(\widehat {K{\rm{AE}}} + \widehat {KCE} = 180^\circ \)
Mà \(\widehat {KC{\rm{D}}} + \widehat {KCE} = 180^\circ \) (hai góc kề bù)
Do đó \(\widehat {K{\rm{AE}}} = \widehat {KC{\rm{D}}}\) hay \(\widehat {K{\rm{AB}}} = \widehat {KC{\rm{D}}}\)
Do tứ giác BKDE nội tiếp đường tròn nên \(\widehat {KD{\rm{E}}} + \widehat {KBE} = 180^\circ \)
Mà \(\widehat {KBA} + \widehat {KBE} = 180^\circ \) (hai góc kề bù)
Do đó \(\widehat {KD{\rm{E}}} = \widehat {KBA}\) hay \(\widehat {{\rm{KBA}}} = \widehat {KDC}\)
Xét ΔDKC và ΔBKA có:
\(\widehat {{\rm{KBA}}} = \widehat {KDC}\) (chứng minh trên)
\(\widehat {K{\rm{AB}}} = \widehat {KC{\rm{D}}}\) (chứng minh trên)
Suy ra (g.g)
Do đó \(\frac{{KC}}{{K{\rm{A}}}} = \frac{{K{\rm{D}}}}{{KB}}\)
Hay \(\frac{{KC}}{{KD}} = \frac{{KA}}{{KB}}\)
Ta có: \(\widehat {BK{\rm{D}}} = \widehat {DKC} + \widehat {BKC}\); \(\widehat {AKC} = \widehat {BKA} + \widehat {BKC}\)
Mà \(\widehat {DKC} = \widehat {BK{\rm{A}}}\), suy ra \(\widehat {DKB} = \widehat {CK{\rm{A}}}\)
Xét ΔKBD và ΔKAC có:
\(\widehat {DKB} = \widehat {CK{\rm{A}}}\) (chứng minh trên)
\(\frac{{KC}}{{KD}} = \frac{{KA}}{{KB}}\) (chứng minh trên)
Suy ra (c.g.c)
Do đó \(\widehat {KB{\rm{D}}} = \widehat {KAC}\)
Hay \(\widehat {KBF} = \widehat {KAF}\)
Suy ra tứ giác AKFB nội tiếp đường tròn
Do đó \(\widehat {BKF} = \widehat {{\rm{BAF}}}\) (2 góc nội tiếp chắn cung BF)
Suy ra \(\widehat {BKF} = \widehat {BAC} = \widehat {B{\rm{D}}C}\) (do \(\widehat {BAC},\widehat {B{\rm{D}}C}\) cùng chắn cung BC) (1)
Ta có: \(\widehat {B{\rm{D}}C} = \widehat {F{\rm{D}}C} = \widehat {FKC}\) (cùng chắn cung FC) (2)
Xét ΔBMC có \(\widehat {MBC} + \widehat {MCB} + \widehat {BMC} = 180^\circ \) (tổng ba góc trong một tam giác)
Mà \(\widehat {MBC} = \widehat {BAC},\widehat {MCB} = \widehat {B{\rm{D}}C}\)(Góc tạo bởi tiếp tuyến và dây cung)
Suy ra \(\widehat {BAC} + \widehat {BDC} + \widehat {BMC} = 180^\circ \) (3)
Từ (1); (2) và (3) suy ra \(\widehat {BKF} + \widehat {FKC} + \widehat {BMC} = 180^\circ \)
Hay \(\widehat {BKC} + \widehat {BMC} = 180^\circ \)
Do đó tứ giác BKCM nội tiếp đường tròn
b) Ta có \(\widehat {BKF} = \widehat {B{\rm{D}}C}\) (chứng minh câu a)
Suy ra \(\widehat {BKF} = \widehat {B{\rm{DE}}} = \widehat {BKE}\) (Do tứ giác DKBE nội tiếp đường tròn)
Mà 2 điểm F và E nằm cùng phía so với BK
Suy ra 3 điểm K; F; E thẳng hàng
Hay F nằm trên KE (*)
Vì \(\widehat {BKF} = \widehat {BAC},\widehat {CKF} = \widehat {B{\rm{D}}C},\widehat {BAC} = \widehat {B{\rm{D}}C}\)
Nên \(\widehat {BKF} = \widehat {CKF}\)
Suy ra \(\widehat {BKE} = \widehat {CKE}\) (Do K; F; E thẳng hàng)
Do đó KE là phân giác của \(\widehat {BKC}\) (4)
Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M
Nên MB = MC
Do đó tam giác MBC cân tại M
Suy ra \(\widehat {MBC} = \widehat {MCB}\)
Xét tứ giác BKCM nội tiếp đường tròn có \(\widehat {MBC} = \widehat {MKC},\widehat {MCB} = \widehat {MKB}\)
Suy ra \(\widehat {MKC} = \widehat {MKB}\)
Do đó KM là phân giác của \(\widehat {BKC}\) (5)
Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)
Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng
Vậy 3 điểm E; M; F thẳng hàng.
Câu 28:
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB kẻ hai tia Ax, By vuông góc với AB. Trên tia Ax và By lần lượt lấy hai điểm C và D sao cho \(\widehat {CO{\rm{D}}} = 90^\circ \) (O là trung điểm của AB). Chứng minh rằng:
a) CD = AC + BD
b) CD là tiếp tuyến của đường tròn đường kính AB
c) \(AC.B{\rm{D}} = \frac{{A{B^2}}}{4}\).
 Xem đáp án
Xem đáp án
Lời giải
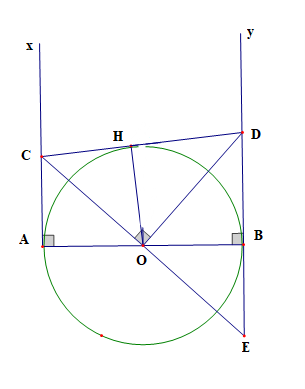
a) Gọi E là giao điểm của CO và BD
Xét ∆ACO và ∆BEO có
\(\widehat {CAO} = \widehat {EBO}\left( { = 90^\circ } \right)\)
AO = BO (giả thiết)
\(\widehat {BOE} = \widehat {AOC}\) (hai góc đối đỉnh)
Suy ra ∆ACO và ∆BEO (g.c.g)
Do đó AC = BE, CO = OE (các cặp cạnh tương ứng)
Xét ∆COD và ∆EOD có
OD là cạnh chung
\(\widehat {CO{\rm{D}}} = \widehat {EOD}\left( { = 90^\circ } \right)\)
CO = OE (chứng minh trên)
Suy ra ∆COD và ∆EOD (c.g.c)
Do đó CD = DE (hai cạnh tương ứng)
Ta có CD = DE = BD + BE = BD + AC
Vậy CD = AC + BD
b) Kẻ OH ⊥ CD
Ta có DC = DE (chứng minh câu a)
Suy ra tam giác DCE cân ở D
Mà DO là đường cao nên DO đồng thời là phân giác của \(\widehat {C{\rm{D}}E}\)
Suy ra \(\widehat {{\rm{CD}}O} = \widehat {O{\rm{D}}E}\)
Xét ∆HOD và ∆BOD có
\(\widehat {{\rm{DHO}}} = \widehat {DBO}\left( { = 90^\circ } \right)\)
OD là cạnh chung
\(H = \widehat {O{\rm{DB}}}\) (chứng minh trên)
Suy ra ∆HOD và ∆BOD (cạnh huyền – góc nhọn)
Do đó OH = OB, HD = BD (các cặp cạnh tương ứng)
Mà OB là bán kính của (O)
Suy ra H thuộc (O)
Lại có OH ⊥ CD nên CD là tiếp tuyến của (O)
c) Xét ∆HOC và ∆AOC có
\(\widehat {{\rm{CHO}}} = \widehat {CAO}\left( { = 90^\circ } \right)\)
OC là cạnh chung
OH = OA (= OB)
Suy ra ∆HOC = ∆AOC (cạnh huyền – cạnh góc vuông)
Do đó HC = AC
Xét tam giác COD vuông tại O có OH ⊥ CD
Theo hệ thức lượng trong tam giác có
OH2 = CH . DH
Ta có: \(AC.B{\rm{D}} = CH.DH = O{H^2} = O{A^2} = {\left( {\frac{{BC}}{2}} \right)^2} = \frac{{B{C^2}}}{4}\)
Vậy \(AC.B{\rm{D}} = \frac{{A{B^2}}}{4}\).
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải
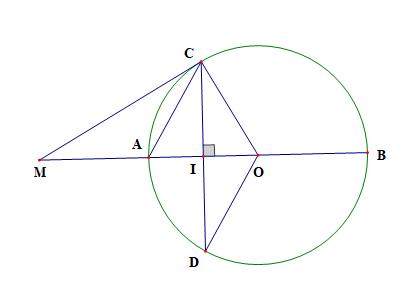
a) Ta có CO, OA, OB là bánh kính, AB là đường kính
![]()
Vì I là trung điểm của OA
![]()
Xét (O) có
AO là một phần của đường kính
CD là dây cung không đi qua tâm
AO ⊥ CD tại I
Suy ra I là trung điểm của CD (quan hệ giữa đường kính và dây cung)

Xét tam giác OIC vuông tại I có
CO2 = CI2 + IO2 (Định lý Pytago)
Hay 102 = CI2 + 52
Suy ra \(CI = 5\sqrt 3 \)
Do đó \(C{\rm{D}} = 2CI = 2.5\sqrt 3 = 10\sqrt 3 \) (cm)
b) Xét tam giác COI có:
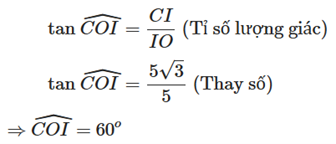
Xét tam giác AOC có OC = OA
Nên tam giác AOC cân tại O
Mà \(\widehat {COA} = 60^\circ \) nên tam giác AOC đều
Do đó OA = OC = AC
Mà OA = OM nên CA = AM = AO
Do đó \(CA = \frac{1}{2}OM\)
Xét tam giác CMO có \(CA = \frac{1}{2}OM\)
Suy ra tam giác COM vuông tại C nên OC ⊥ CM
Xét (O) có OC ⊥ CM, OC là bán kính
Suy ra CM là tiếp tuyến của (O)
Vậy MC là tiếp tuyến của đường tròn (O).
Câu 30:
Cho tam giác ABC cân tại A có đường cao AH, kẻ BK vuông góc AC. Chứng minh:
\(\frac{1}{{B{K^2}}} = \frac{1}{{4B{C^2}}} + \frac{1}{{4A{H^2}}}\).
 Xem đáp án
Xem đáp án
Lời giải
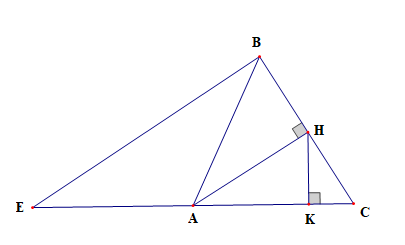
Trên tia CA lấy E sao cho A là trung điểm của CE
Vì tam giác ABC cân tại A nên BA = AC
Suy ra \(BA = \frac{1}{2}CE\)
Xét tam giác BCE có BA là trung tuyến và \(BA = \frac{1}{2}CE\)
Suy ra tam giác EBC vuông tại E
Hay BC ⊥ BE
Mà BC ⊥ AH nên AH // BE (quan hệ từ vuông góc đến song song)
Xét tam giác EBC có AH // BE và A là trung điểm của CE
Suy ra \[{\rm{A}}H = \frac{1}{2}BE\]
Xét tam giác BEC vuông tại B có BK là đường cao
Suy ra \(\frac{1}{{B{K^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{B{E^2}}}\)
Do đó \(\frac{1}{{B{K^2}}} = \frac{1}{{4B{C^2}}} + \frac{1}{{4A{H^2}}}\)
Vậy \(\frac{1}{{B{K^2}}} = \frac{1}{{4B{C^2}}} + \frac{1}{{4A{H^2}}}\).
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Phương trình hoành giao điểm là
\(\frac{{2{\rm{x}} + 1}}{{x + 1}} = - x - 1\) (x≠ – 1)
⇔ 2x + 1 = (x + 1)( – x – 1)
⇔ 2x + 1 = – x2 – 2x – 1
⇔ x2 + 4x + 2 = 0
Gọi x1, x2 là hai nghiệm của phương trình trên
Theo Vi – ét ta có:
x1 + x2 = –4 và x1 . x2 = 2
Tọa độ các điểm A(x1; y1) và B(x2; y2)
Độ dài đoạn thẳng AB là
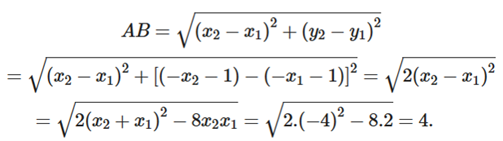
Vậy ta chọn đáp án A.
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
Tập xác định: D = ℝ
Ta có: \(y = c{\rm{o}}{{\rm{s}}^2}x - 1 = \frac{{1 + c{\rm{os2x}}}}{2} - 1 = \frac{1}{2}cos2{\rm{x}} - \frac{1}{2}\)
Với mọi x ∈ ℝ thì x + π ∈ ℝ
\(f\left( {x + \pi } \right) = \frac{1}{2}cos\left( {2{\rm{x}} + 2\pi } \right) - \frac{1}{2} = \frac{1}{2}cos2{\rm{x}} - \frac{1}{2} = f\left( {\rm{x}} \right)\)
Suy ra hàm số tuần hoàn với chu kì T = π
Vậy hàm số tuần hoàn với chu kì T = π.
Câu 33:
Cho mệnh đề: “ ∀ x ∈ ℝ, x2 + 3x + 5 > 0”. Mệnh đề phủ định của mệnh đề trên là:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Mệnh đề phủ định của ∀ x ∈ R, x2 + 3x + 5 > 0 là ∃ x ∈ R, x2 + 3x + 5 ≤ 0
Vậy ta chọn đáp án A.
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là D
Ta có: Pn = n! = n(n – 1)(n – 2) ... . 2 . 1. Do đó B và C đúng.
\[{\rm{A}}_n^k = \frac{{n!}}{{\left( {n - k} \right)!}} = n\left( {n - 1} \right)...\left( {n - k + 1} \right)\]. Do đó A đúng D sai.
Vậy ta chọn đáp án D.
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: B = n4 + 64 = n4 + 16n2 + 64 – 16n2
= (n2 + 8)2 – (4n)2 = (n2 – 4n + 8)(n2 + 4n + 8)
Suy ra B = n4 + 64 không phải là số nguyên tố với mọi n thuộc Z.
Câu 36:
Cho biểu thức \(P = \sqrt {\frac{{{{\left( {{x^2} - 3} \right)}^2} + 12{{\rm{x}}^2}}}{{{x^2}}}} + \sqrt {{{\left( {x + 2} \right)}^2} - 8{\rm{x}}} \)
a) Rút gọn P.
b) Tìm giá trị nguyên của x để P ∈ ℤ.
 Xem đáp án
Xem đáp án
Lời giải
a) Điều kiện xác định x ≠ 0
Ta có:
\(P = \sqrt {\frac{{{{\left( {{x^2} - 3} \right)}^2} + 12{{\rm{x}}^2}}}{{{x^2}}}} + \sqrt {{{\left( {x + 2} \right)}^2} - 8{\rm{x}}} \)

b) Với x ≠ 0, ta có: \(P \in \mathbb{Z} \Leftrightarrow \left| {\frac{{{x^2}}}{x} + \frac{3}{x}} \right| + \left| {x - 2} \right| \in \mathbb{Z}\)
\( \Leftrightarrow \frac{3}{x} \in \mathbb{Z}\) ⇔ 3 ⋮ x
⇔ x ∈ Ư(3) = {1; 3; –1; –3}
Vậy x ∈ {1; 3; –1; –3} thì P ∈ Z.
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
+) TH1: cosx = 0 hay \[{\rm{x}} = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\]
Suy ra sin2x = 1
Khi đó \(\sqrt 3 .0 - 1.0{\rm{ + 1}} = 1\) (luôn đúng)
Do đó \[{\rm{x}} = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\] là nghiệm của phương trình
+) TH1: cosx ≠ 0
Chia cả 2 vế của phương trình cho cos2x ta có:
\(\sqrt 3 - \tan x + {\tan ^2}x = \frac{1}{{co{s^2}x}}\)
\( \Leftrightarrow \sqrt 3 - \tan x + {\tan ^2}x = 1 + {\tan ^2}x\)
\( \Leftrightarrow \sqrt 3 - 1 = \tan x\)
\( \Leftrightarrow x = \arctan \left( {\sqrt 3 - 1} \right) + \frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)\)
Vậy nghiệm của phương trình là \(x = \frac{\pi }{2} + k\pi ,x = \arctan \left( {\sqrt 3 - 1} \right) + \frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)\).
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Điều kiện xác định n ≠ –1
Để phân số \(\frac{3}{{n + 1}}\)là số nguyên thì 3 ⋮ n + 1
Suy ra n + 1 ∈ {–1; –3; 1; 3}
Hay n ∈ {–2; –4; 0; 2} (thỏa mãn)
Vậy n ∈ {–2; –4; 0; 2} thì phân số \(\frac{3}{{n + 1}}\) có giá trị là một số nguyên.
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
Điều kiện xác định n ≠ 1
Ta có: \[{\rm{A}} = \frac{n}{{n - 1}} = \frac{{n - 1 + 1}}{{n - 1}} = 1 + \frac{1}{{n - 1}}\]
Để phân số \[{\rm{A}} = \frac{n}{{n - 1}}\]là số nguyên thì 1 ⋮ n – 1
Suy ra n – 1 ∈ {–1; 1}
Hay n ∈ {0; 2} (thỏa mãn)
Vậy n ∈ {0; 2} thì phân số \[{\rm{A}} = \frac{n}{{n - 1}}\] là một số nguyên.
Câu 40:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Ta có:
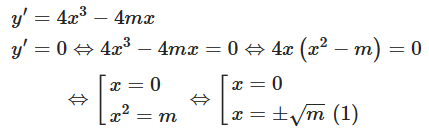
Hàm số y = f(x) có 3 cực trị
⇔ y’ = 0 có 3 nghiệm phân biệt
⇔ phương trình (1) có 2 nghiệm phân biệt khác 0
⇔ m > 0
Gọi 3 điểm phân biệt của hàm số là
\(A\left( {0;a} \right),B\left( { - \sqrt m ;b} \right),C\left( {\sqrt m ;c} \right)\). Khi đó:
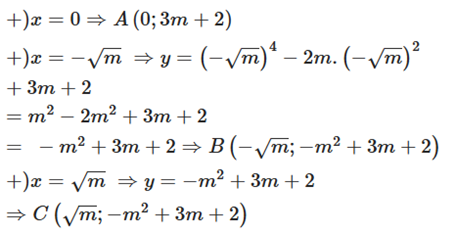
Ta luôn có AB = AC nên tam giác ABC đều
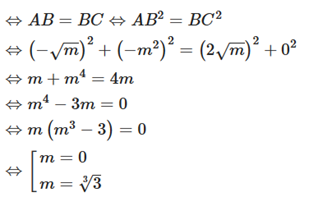
Mà m > 0 nên \(m = \sqrt[3]{3}\)
Vậy ta chọn đáp án A.
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là C
Ta có:
∆ = (–3)2 – 4 . (–1) = 13 > 0
Suy ra phương trình có 2 nghiệm phân biệt là:
\[{{\rm{x}}_1} = \frac{{ - 3 + \sqrt {13} }}{2},{x_2} = \frac{{ - 3 - \sqrt {13} }}{2}\]
Vậy ta chọn đáp án C.
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có: \(y = \frac{{2{\rm{x}} + 4}}{{x - 3}} = \frac{{2{\rm{x}} - 6 + 10}}{{x - 3}} = \frac{{2\left( {x - 3} \right) + 10}}{{x - 3}} = 2 + \frac{{10}}{{x - 3}}\)
Có y ∈ ℤ ⇔ 10 ⋮ x – 3
Suy ra x – 3 ∈ Ư(10) = {1; 2; 5; 10; –1; –2; –5; –10}
Hay x ∈ {4; 5; 8; 13; 2; 1; –2; –7}
Khi đó y ∈ {12; 7; 4; 3; –8; –3; 0; 1}
Vậy ta chọn đáp án C.
Câu 43:
 Xem đáp án
Xem đáp án
Lời giải
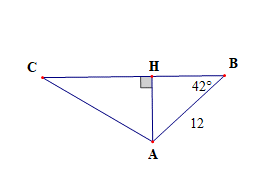
Kẻ AH ⊥ BC
Xét tam giác ABH có
AH = AB . sinB = 12 . sin42° ≈ 8 (cm)
Áp dụng định lý Pytago trong tam giác AHB vuông tại H có
BH2 = AB2 – AH2 = 122 – 82 = 80
Suy ra \(BH = 4\sqrt 5 \) (cm)
Khi đó \(CH = BC - BH = 22 - 4\sqrt 5 \)
Áp dụng định lý Pytago trong tam giác AHC vuông tại H có
AC2 = AH2 + CH2
Suy ra \[{\rm{A}}C = \sqrt {{8^2} + {{\left( {22 - 4\sqrt 5 } \right)}^2}} \approx 15,3\] (cm)
Mà \[\sin C = \frac{{AH}}{{AC}} = \frac{8}{{15,3}}\]
Suy ra \(\widehat C \approx 31^\circ \)
Xét tam giác ABC có
\(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {BAC} + 42^\circ + 31^\circ = 180^\circ \)
Suy ra \(\widehat {BAC} = 107^\circ \)
Vậy \(\widehat {BAC} = 107^\circ ;\widehat C = 31^\circ ;AC = 15,3cm.\)
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án dúng là: D
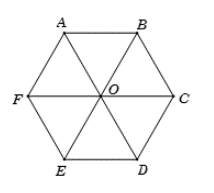
• Ta có OABC là hình bình hành
Suy ra \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OE} = \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow 0 \) (vì O là trung điểm của BE)
Do đó A đúng
• Ta có: \(\overrightarrow {BC} = \overrightarrow {AO} \) ( ABCO là hình bình hành)
\(\overrightarrow {F{\rm{E}}} = \overrightarrow {O{\rm{D}}} \) (FODE là hình bình hành)
Suy ra \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {O{\rm{D}}} = \overrightarrow {A{\rm{D}}} \)
Do đó B đúng
• Ta có OABC là hình bình hành
Suy ra \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OB} = \overrightarrow {OB} + \overrightarrow {OB} = \overrightarrow {EB} \)
Do đó C đúng
Vậy ta chọn đáp án D.
Câu 45:
 Xem đáp án
Xem đáp án
Lời giải
Để hai đường thẳng y = (2m – 1)x – 3 và y = mx + m2 – 4m cắt nhau tại một điểm nằm trên trục tung thì
\(\left\{ \begin{array}{l}2m - 1 \ne m\\ - 3 = {m^2} - 4m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\{m^2} - 4m + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\\left[ \begin{array}{l}m = 1\\m = 3\end{array} \right.\end{array} \right. \Leftrightarrow m = 3\)
Vậy m = 3 thì đường thẳng y = (2m – 1)x – 3 và y = mx + m2 – 4m cắt nhau tại một điểm nằm trên trục tung.
Câu 46:
 Xem đáp án
Xem đáp án
Lời giải
Các số có 3 chữ số khác nhau là:
123, 132, 231, 213, 321, 312
Tổng của 6 số trên là:
123 + 132 + 213 + 231 + 321 + 312 = 1332.
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
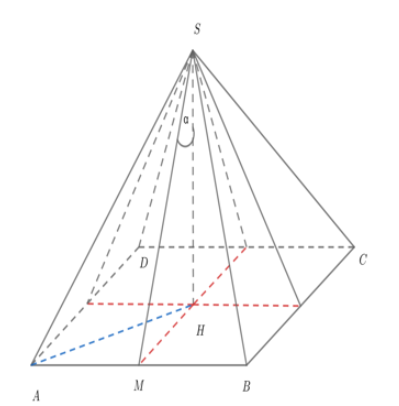
Vì góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α nên H là tâm đường tròn nội tiếp ABCD
Vì các cạnh bên của hình chóp S.ABCD đều bằng a nên H là tâm đường tròn ngoại tiếp ABCD
Suy ra ABCD là hình vuông
Do đó hình chóp S.ABCD là hình chóp đều
Ta có:
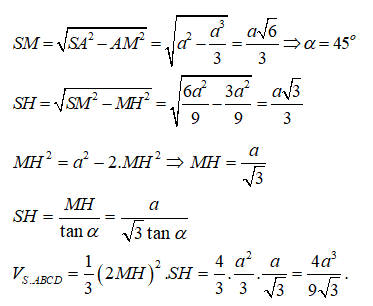
Vậy ta chọn đáp án D.
Câu 48:
Cho tam giác ABC cân tại B. Trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = CN. Kẻ BH ⊥ AC tại H.
a) Chứng minh AH = HC.
b) Chứng minh ∆BAN = ∆BCM.
c) Gọi O là giao điểm của AN và CM. Chứng minh 3 điểm B, O, H thẳng hàng.
 Xem đáp án
Xem đáp án
Lời giải
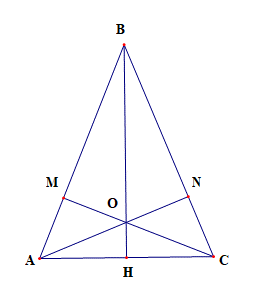
a) Xét tam giác ABC cân tại B có BH là đường cao nên đồng thời là đường trung tuyến
Do đó AH = CH.
b) Vì tam giác ABC cân tại B nên AB = BC
Ta có: AB = AM + MB; BC = BN + NC
Mà AM = CN (giả thiết) nên BM = BN
Xét ∆BAN và ∆BCM có
BM = BN (chứng minh trên);
Chung góc \(\widehat {ABC}\);
AB = BC (chứng minh trên)
Suy ra ∆BAN = ∆BCM (c.g.c)
c) Vì ∆BAN = ∆BCM (chứng minh câu b)
Nên \(\widehat {BAN} = \widehat {BCM}\) (hai góc tương ứng)
Xét tam giác AMO có
\(\widehat {AM{\rm{O}}} + \widehat {AOM} + \widehat {MAO} = 180^\circ \) (tổng ba góc trong một tam giác)
Xét tam giác CNO có
\(\widehat {{\rm{CNO}}} + \widehat {CON} + \widehat {NCO} = 180^\circ \) (tổng ba góc trong một tam giác)
Mà \(\widehat {MAO} = \widehat {NCO},\widehat {MOA} = \widehat {NOC}\)
Suy ra \(\widehat {AM{\rm{O}}} = \widehat {CNO}\)
Xét ∆MOA và ∆NOC có
\(\widehat {AM{\rm{O}}} = \widehat {CNO}\) (chứng minh trên);
AM = CN (giả thiết);
\(\widehat {MAO} = \widehat {NCO}\) (chứng minh trên)
Suy ra ∆MOA = ∆NOC (g.c.g)
Do đó OA = OC (hai cạnh tương ứng)
Xét ∆BOA và ∆BOC có
OA = OC (chứng minh trên);
\(\widehat {BAO} = \widehat {BCO}\) (chứng minh trên);
BA = BC (chứng minh câu b)
Suy ra ∆BOA = ∆BOC (c.g.c)
Do đó \(\widehat {ABO} = \widehat {CBO}\) (hai góc tương ứng)
Suy ra BO là tia phân giác của \(\widehat {ABC}\) (1)
Xét tam giác ABC cân tại B có
BH là đường cao
Suy ra BH là tia phân giác của \(\widehat {ABC}\) (2)
Từ (1) và (2) suy ra ba điểm 3 điểm B, O, H thẳng hàng.
