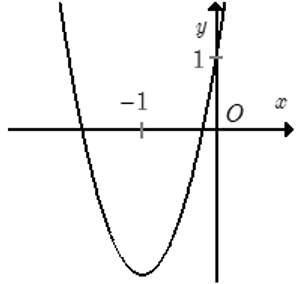
Cho hàm số f(x) = ax2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
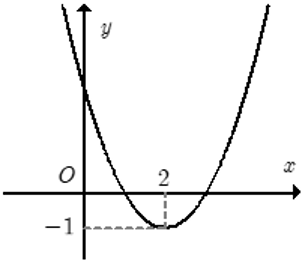
A. 0 < m < 1
B. m > 3
C. m = −1, m = 3
D. −1 < m < 0
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: A
Ta có
Từ đó suy ra cách vẽ đồ thị hàm số (C) từ đồ thị hàm số y = f(x) như sau:
+ Giữ nguyên đồ thị y = f(x) phía trên trục hoành.
+ Lấy đối xứng phần đồ thị y = f(x) phía dưới trục hoành qua trục hoành (bỏ phần dưới).
Kết hợp hai phần ta được đồ thị hàm số y =| f(x)| như hình vẽ.
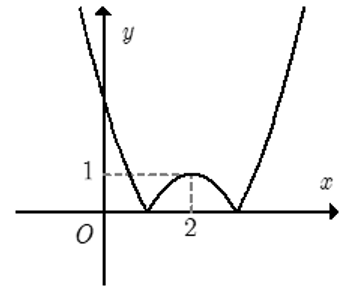
Phương trình |f(x)| = m là phương trình hoành độ giao điểm của đồ thị hàm số
y = |f(x)| và đường thẳng y = m (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có yêu cầu bài toán ⇔ 0 < m < 1.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên. Khẳng định nào sau đây đúng ?
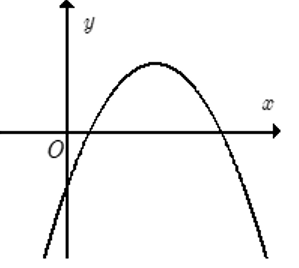
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
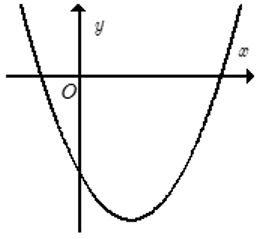
Khẳng định nào sau đây đúng ?
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 5 tại
x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = a2 + b2 + c2.
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.
Nếu hàm số y = ax2 + bx + c có a < 0, b > 0 và c > 0 thì đồ thị của nó có dạng
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Xác định parabol (P): y = 2x2 + bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.
Cho hàm số y = ax2 + bx + c (a > 0). Khẳng định nào sau đây là sai?
Cho hàm số y = ax2 + bx + c có đồ thị (P) như hình vẽ.
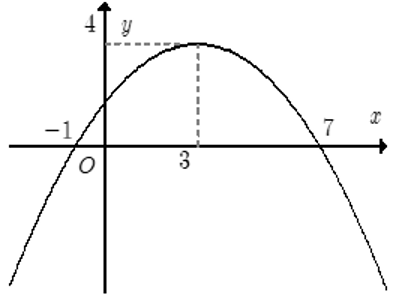
Khẳng định nào sau đây là sai?
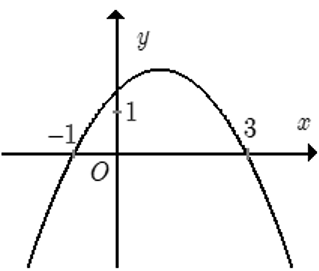
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x2 − 4x + 3 trên đoạn [−2; 1].