Giải các phương trình
a) |3x - 2| = 2x + 3 ;
b) |2x - 1| = |-5x - 2| ;
c)
d) |2x + 5| = x2 + 5x + 1.
 Giải bởi Vietjack
Giải bởi Vietjack
a) |3x – 2| = 2x + 3 (1)
Tập xác định: D = R.
+ Nếu 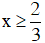
Giá trị x = 5 thỏa mãn điều kiện nên x = 5 là một nghiệm của phương trình (3).
+ Nếu 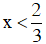
Giá trị 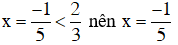
Vậy phương trình có hai nghiệm x = 5 và
b) |2x - 1| = |-5x - 2| (2)
Tập xác định D = R.
Ta có:
Vậy phương trình có hai nghiệm 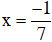
+ Xét x > –1, khi đó x + 1 > 0 nên |x + 1| = x + 1.
Khi đó pt (3)
+ Xét x < –1, khi đó x + 1 < 0 nên |x + 1| = –x – 1.
Khi đó pt (3)
(không thỏa mãn điều kiện x < –1).
Vậy phương trình có hai nghiệm là
d) |2x + 5| = + 5x + 1 (4)
Tập xác định: D = R.
+ Xét 2x + 5 ≥ 0 ⇔ 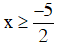
Khi đó pt (4) ⇔ 2x + 5 = + 5x + 1
⇔ + 3x – 4 = 0
⇔ (x + 4)(x – 1) = 0
⇔ x = –4 (không thỏa mãn) hoặc x = 1 (thỏa mãn)
+ Xét 2x + 5 < 0 ⇔ 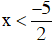
Khi đó pt (4) ⇔ –2x – 5 = + 5x + 1
⇔ + 7x + 6 = 0
⇔ (x + 1)(x + 6) = 0
⇔ x = –1 (không thỏa mãn) hoặc x = –6 (thỏa mãn).
Vậy phương trình có hai nghiệm x = 1 hoặc x = –6.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Giải và biện luận các phương trình sau theo tham số m:
a) m(x - 2) = 3x + 1 ;
b) m2 x+ 6 = 4x + 3m ;
c) (2m + 1)x - 2m = 3x - 2;
Cho phương trình 3 - 2(m + 1)x + 3m - 5 = 0
Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.
Có hai rổ quýt chứa số quýt bằng nhau. Nếu lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ hai bằng 1/3 của bình phương số quả còn lại ở rổ thứ nhất. Hỏi số quả quýt ở mỗi rổ lúc ban đầu là bao nhiêu?
Giải các phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ ba)
a) - 5x - 4 = 0 ; b) -3 + 4x + 2 = 0
c) 3 + 7x + 4 = 0 ; d) 9 - 6x - 4 = 0.