Trong không gian Oxyz cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 27\). Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua hai điểm \(A\left( {0;0; - 4} \right)\), \(B\left( {2;0;0} \right)\) và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) sao cho khối nón có đỉnh là tâm của \(\left( S \right)\), đáy là hình tròn \(\left( C \right)\) có thể tích lớn nhất. Biết mặt phẳng \(\left( \alpha \right)\) có phương trình dạng \(ax + by - z + c = 0\), khi đó \(a - b + c\) bằng:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Ta có mặt cầu \(\left( S \right)\) có tâm \(I\left( {1; - 2;3} \right)\) bán kính \(R = 3\sqrt 3 \)
Vì \(A \in \left( \alpha \right) \Rightarrow 4 + c = 0 \Leftrightarrow c = - 4\) và \(A,B \in \left( \alpha \right) \Rightarrow \overrightarrow {AB} .\overrightarrow {{n_\alpha }} = 0 \Leftrightarrow 2{\rm{a}} - 4 = 0 \Leftrightarrow a = 2\).
Suy ra \(d\left( {I,(\alpha )} \right) = \frac{{\left| {2b + 5} \right|}}{{\sqrt {{b^2} + 5} }}\)
Gọi r là bán kính đường tròn \(\left( C \right)\) ta có \({r^2} = {R^2} - {d^2}\left( {I,(\alpha )} \right) = 27 - {d^2}\) với \(0 < d < 3\sqrt 3 \).
Khi đó thể tích khối nón \(V = \frac{1}{3}\pi {r^2}d\) để V lớn nhất thì \(f\left( d \right) = {r^2}.d = \left( {27 - {d^2}} \right)d\) lớn nhất.
Xét hàm \(f\left( d \right) = 27{\rm{d}} - {d^3}\) với \(0 < d < 3\sqrt 3 \)
Ta có \(f'\left( d \right) = - 3{{\rm{d}}^2} + 27 = 0 \Leftrightarrow d = \pm 3\) suy ra \(\mathop {\max }\limits_{\left( {0;3\sqrt 3 } \right)} \left[ {f\left( d \right)} \right] = f\left( 3 \right) = 54\) đạt được khi
\(d = 3 \Leftrightarrow \frac{{\left| {2b + 5} \right|}}{{\sqrt {{b^2} + 5} }} = 3 \Leftrightarrow 5\left( {{b^2} - 4b + 4} \right) = 0 \Leftrightarrow b = 2\).
Vậy giá trị biểu thức \(a - b + c = - 4\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?
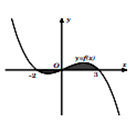
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) với trục Ox nằm phía trên và phía dưới trục Ox lần lượt là 3 và 1. Khi đó \(\int\limits_{ - 2}^3 {f\left( x \right)d{\rm{x}}} \) bằng
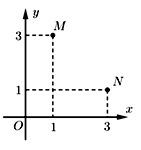
Trong hình vẽ bên điểm M biểu diễn số phức \({z_1}\), điểm N biểu diễn số phức \({z_2}\). Hỏi trung điểm của đoạn MN là điểm biểu diễn hình học của số phức nào sau đây
Trong hệ trục Oxyz cho mặt cầu có phương trình \({x^2} + {y^2} + {z^2} - 2{\rm{z}} + 4y + 6{\rm{z}} - 1 = 0\). Xác định tâm và bán kính của mặt cầu.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng
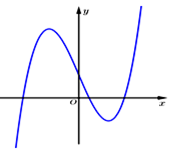
Đường cong ở hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Cho hình lập phương \(ABC{\rm{D}}{\rm{.A'B'C'D'}}\) có diện tích tam giác \(AC{\rm{D'}}\) bằng \({a^2}\sqrt 3 \). Tính thể tích V của khối lập phương.
Cho hàm số \(y = f\left( x \right){\rm{ }}\left( C \right)\) xác định trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( {1 - x} \right) + f\left( {1 - {x^2}} \right) = x + 1{\rm{ }}\left( {\forall x \in \mathbb{R}} \right)\). Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung có dạng \(y = ax + b\). Giá trị của biểu thức \(T = 5{\rm{a}} + 2b\) bằng
Gọi \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = 2{\rm{x}} + {e^x}\) thỏa mãn \(F\left( 0 \right) = 2019\). Tính \(F\left( 1 \right)\).
Số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{2}}}\left( {x - 3} \right) \ge {\log _{\frac{1}{2}}}4\) là
Tìm m để phương trình \(\log _2^2x - {\log _2}{x^2} + 3 = m\) có nghiệm \(x \in \left[ {1;8} \right]\).
Có 9 tấm thẻ được đánh số từ 1 đến 9. Chọn ngẫu nhiên ra 2 tấm thẻ bất kỳ. Tính xác suất để tích của hai số trên 2 tấm thẻ đã lấy là một số chẵn.
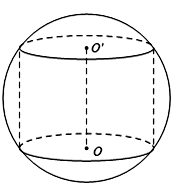
Cho khối cầu \(\left( S \right)\) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; - 1;2} \right)\) và mặt phẳng \(\left( P \right):2{\rm{x}} - y + z + 1 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua điểm A và song song với \(\left( P \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là
Phương trình đường thẳng song song với đường thẳng \(d:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{z}{{ - 1}}\) và cắt hai đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y + 1}}{1} = \frac{{z - 2}}{{ - 1}}\) và \({d_2}:\frac{{x - 1}}{{ - 1}} = \frac{{y - 2}}{1} = \frac{{z - 3}}{3}\) là