Cho $\int\limits_0^2 {f\left( x \right)dx} = 3$ và $\int\limits_0^2 {g\left( x \right)dx} = - 1$. Giá trị của $\int\limits_0^2 {\left[ {f\left( x \right) - 5g\left( x \right) + x} \right]dx}$ bằng:

Trong không gian với hệ tọa độ Oxyz cho đường thẳng ${d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\\z = 3\end{array} \right.$ và ${d_2}:\left\{ \begin{array}{l}x = 1\\y = 2 + 7t'\\z = 3 + t'\end{array} \right.$. Phương trình đường phân giác của góc tù giữa ${d_1}$ và ${d_2}$ là:

Một lớp có 19 học sinh nữ và 25 học sinh nam. Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác tham gia một hoạt động của Đoàn trường. Xác suất để 4 học sinh được chọn có cả nam và nữ bằng (làm tròn đến chữ số thập phân thứ 4).

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

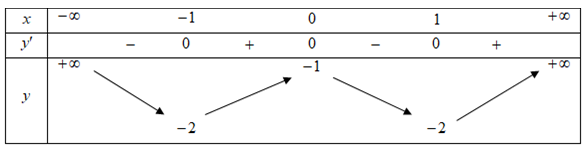
Số điểm cực tiểu của hàm số $g\left( x \right) = 2{f^3}\left( x \right) + 4{f^2}\left( x \right) + 1$ là:

Trong không gian Oxyz, có tất cả bao nhiêu giá trị nguyên của m để ${x^2} + {y^2} + {z^2} + 2\left( {m + 2} \right)x - 2\left( {m - 1} \right)z + 3{m^2} - 5 = 0$ là phương trình của một mặt cầu?

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)$ với mọi $x \in \mathbb{R}$. Có bao nhiêu số nguyên m thuộc đoạn $\left[ { - 2019;2019} \right]$ để hàm số $g\left( x \right) = f\left( {1 - x} \right)$ nghịch biến trên khoảng $\left( { - \infty ; - 1} \right)$?

Trong không gian Oxyz, cho $\overrightarrow {OA} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k$, điểm $B\left( {3; - 4;1} \right)$ và điểm $C\left( {2;0; - 1} \right)$. Tọa độ trọng tâm của tam giác ABC là:

Cho tập A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử?

Kí hiệu ${z_1}$ và ${z_2}$ là hai nghiệm phức của phương trình ${z^2} + z + 1 = 0$. Tính $P = z_1^2 + z_2^2 + {z_1}{z_2}$.

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và $\widehat {ABC} = 60^\circ$. Hình chiếu vuông góc của điểm S lên mặt phẳng $\left( {ABCD} \right)$ trùng với trọng tâm tam giác ABC. Gọi $\varphi$ là góc giữa đường thẳng SB với mặt phẳng $\left( {SCD} \right)$, tính $\sin \varphi$ biết rằng $SB = a$.

Cho a là số thực dương khác 5. Tính $I = {\log _{\frac{a}{5}}}\left( {\frac{{{a^3}}}{{125}}} \right)$.

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left( P \right):2x - 4y + 6z - 1 = 0$. Mặt phẳng $\left( P \right)$ có một vectơ pháp tuyến là:

Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E, F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng $\left( {AEF} \right)$ cắt khối lập phương đã cho thành hai phần, gọi ${V_1}$ là thể tích khối chứa điểm A’ và ${V_2}$ là thể tích khối chứa điểm C’. Khi đó $\frac{{{V_1}}}{{{V_2}}}$ là:

Cho z và w là các số phức thỏa mãn các điều kiện $z\left( {w + 1} \right) + iw - 1 = 0,\left| {w + 2} \right| = 1$. Giá trị nhỏ nhất của biểu thức $T = \left| {z - 1 - 3i} \right|$ bằng:

Cho hàm số $y = f\left( x \right)$ liên tục và có đạo hàm trên $\mathbb{R}$ thỏa mãn $f\left( 2 \right) = - 2;\int\limits_0^2 {f\left( x \right)dx} = 1$. Tính tích phân $I = \int\limits_{ - 1}^3 {f'\left( {\sqrt {x + 1} } \right)dx}$.