Cho số phức nguyên dương. Có bao nhiêu giá trị để z là số thuần ảo?
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Ta có
+ Với thì
+ Với thì
+ Với thì
+ Với thì
Vậy để z là số thuần ảo thì mà
Nên
Vậy có tất cả giá trị của k thỏa mãn điều kiện, tức cũng có 25 giá trị của m thỏa mãn điều kiện đề bài.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
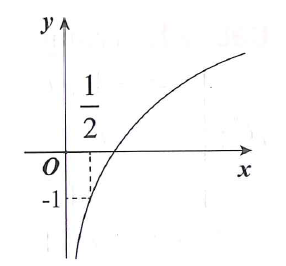
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Cho phương trình trong đó m là tham số phức. Giá trị của m để phương trình có hai nghiệm thỏa mãn là:
Gọi A, B là hai điểm thuộc hai nhánh khác nhau trên đồ thị (C) của hàm số độ dài ngắn nhất của đoạn thẳng AB là
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và Khẳng định nào sau đây là đúng?
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai điểm Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi là giao điểm của d với đường thẳng Giá trị bằng