Câu hỏi:

19/07/2024 179

Cho $f (x) = x^{2} - 4 x + 3$ . Trong các mệnh đề sau, mệnh đề đúng là:

A. $f (x) < 0, \forall x \in (- \infty; 1] \cup [3; + \infty);$

B. $f (x) \leq 0, \forall x \in [1; 3];$

Đáp án chính xác

C. $f (x) \geq 0, \forall x \in (- \infty; 1) \cup (3; + \infty);$

D. $f (x) > 0, \forall x \in [1; 3] .$

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: B

Ta có : $f (x) = x^{2} - 4 x + 3 = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$ .

Bảng xét dấu

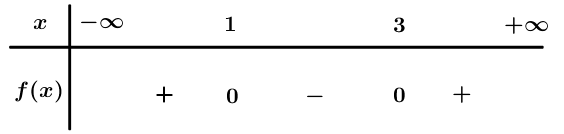
Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow 1 \leq x \leq 3$ .

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Số giá trị nguyên của x để tam thức $f (x) = 2 x^{2} - 7 x - 9$ nhận giá trị âm là

Xem đáp án » 13/09/2022 328

Câu 2:

Tam thức bậc hai $f (x) = 2 x^{2} + 2 x + 5$ nhận giá trị dương khi và chỉ khi

Xem đáp án » 13/09/2022 198

Câu 3:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ . Điều kiện để $f (x) \geq 0, \forall x \in ℝ$

Xem đáp án » 13/09/2022 180

Câu 4:

Tam thức bậc hai $f (x) = (1 - \sqrt{2}) x^{2} + (5 - 4 \sqrt{2}) x - 3 \sqrt{2} + 6$

Xem đáp án » 13/09/2022 177

Câu 5:

Tam thức bậc hai $f (x) = x^{2} + (1 - \sqrt{3}) x - 8 - 5 \sqrt{3}$ :

Xem đáp án » 13/09/2022 175

Câu 6:

Tam thức bậc hai $f (x) = - x^{2} + 5 x - 6$ nhận giá trị dương khi và chỉ khi

Xem đáp án » 13/09/2022 175

Câu 7:

Tam thức bậc hai $f (x) = - x^{2} + 3 x - 2$ nhận giá trị không âm khi và chỉ khi

Xem đáp án » 13/09/2022 174

Câu 8:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ . Điều kiện để $f (x) < 0, \forall x \in ℝ$ là:

Xem đáp án » 13/09/2022 173

Câu 9:

Tam thức bậc hai $f (x) = x^{2} + (\sqrt{5} - 1) x - \sqrt{5}$ nhận giá trị dương khi và chỉ khi

Xem đáp án » 13/09/2022 173

Câu 10:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ . Điều kiện để $f (x) > 0, \forall x \in ℝ$ là

Xem đáp án » 13/09/2022 158

Câu 11:

Dấu của tam thức bậc hai: $f (x) = - x^{2} + 5 x - 6$ được xác định như sau:

Xem đáp án » 13/09/2022 157

Câu 12:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ có $Δ = b^{2} - 4 a c < 0$ . Khi đó mệnh đề nào đúng?

Xem đáp án » 13/09/2022 153

Câu 13:

Cho các tam thức $f (x) = 2 x^{2} - 3 x + 4; g (x) = - x^{2} + 3 x - 4; h (x) = 4 - 3 x^{2}$ . Số tam thức đổi dấu trên $ℝ$ là:

Xem đáp án » 13/09/2022 153

Câu 14:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ . Điều kiện để $f (x) \leq 0, \forall x \in ℝ$ là

Xem đáp án » 13/09/2022 151

Xem thêm các câu hỏi khác »

Hỏi bài

Đề thi liên quan

Xem thêm »

Trắc nghiệm Phương trình đường thẳng có đáp án

5 đề 5625 lượt thi Thi thử
Trắc nghiệm Hàm số bậc hai có đáp án

5 đề 4605 lượt thi Thi thử
Trắc nghiệm Tổng và hiệu của hai Vecto có đáp án

5 đề 4255 lượt thi Thi thử
Trắc nghiệm Phương trình đường tròn có đáp án

5 đề 4243 lượt thi Thi thử
Trắc nghiệm Mệnh đề có đáp án

5 đề 4042 lượt thi Thi thử
Trắc nghiệm Các định nghĩa Vecto có đáp án

4 đề 3844 lượt thi Thi thử
Trắc nghiệm Phương trình quy về phương trình bậc nhất, bậc hai có đáp án

5 đề 3649 lượt thi Thi thử
Trắc nghiệm Toán 10 Hàm số có đáp án

5 đề 3609 lượt thi Thi thử
Trắc nghiệm Tích vô hướng của hai vecto có đáp án

5 đề 3433 lượt thi Thi thử
Trắc nghiệm Hệ trục tọa độ có đáp án

4 đề 3388 lượt thi Thi thử

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho fx=x2−4x+3. Trong các mệnh đề sau, mệnh đề đúng là:

A. fx<0,∀x∈−∞;1∪3;+∞;

B. fx≤0,∀x∈ 1;3 ;

C. fx≥0,∀x∈−∞;1∪3;+∞;

D. fx>0,∀x∈ 1;3 .