Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (Phần 12)
-
457 lượt thi
-
182 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Sử dụng máy tính ta bấm được: \(x = {x_1} + {x_2} = x = 8\cos \left( {\pi t + \frac{\pi }{6}} \right)\)
Đáp án đúng: C
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì dao động của con lắc đặt trong chân không: \(T = 2\pi \sqrt {\frac{\ell }{g}} \)
Chu kì dao động của con lắc đặt trong không khí: \(T' = 2\pi \sqrt {\frac{\ell }{{g'}}} \)
Lực đẩy Archimed có hướng thẳng đứng lên trên nên:
\(g' = g - \frac{{{F_A}}}{m} = g - \frac{{{D_{kk}}Vg}}{{DV}} = g - \frac{{{D_{kk}}g}}{D}\)
\( \Rightarrow \frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{1}{{1 - \frac{{{D_{kk}}}}{D}}}} = 1,00075 \Rightarrow T' = 1,00075.2 = 2,00015\left( s \right)\)
Đáp án đúng: B
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(T = \frac{{2\pi }}{\omega } = 2\left( s \right)\)
Tại \(t = 0:\left\{ \begin{array}{l}x = 5\\v = 0\end{array} \right.\)
Sử dụng đường tròn lượng giác xác định được, vật qua VTCB lần thứ ba vào thời điểm: \(t = \frac{T}{4} + T = 2,5\left( s \right)\)
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
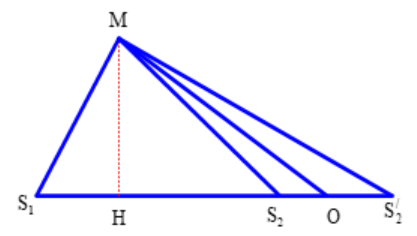
Xét \(\Delta M{S_1}{S_2}\)có \(M{S_1} = 16\left( {cm} \right);M{S_2} = 25\left( {cm} \right)\)
Ta có: \({S_1}{S_2} = {S_1}H + {S_2}H = \sqrt {{{16}^2} - M{H^2}} + \sqrt {{{25}^2} - M{H^2}} = 20\)
\( \Rightarrow MH = 15,98\left( {cm} \right) \Rightarrow M{S'_2} = 33,3\,cm\)
Gọi O là điểm nằm trong khoảng S2S'2 để đặt vị trí nguồn S2.
Tại M có cực đại giao thoa: \(MO - M{S_1} = k\lambda \)
Vì O nằm trên khoảng \({S_2}{S'_2} \Rightarrow M{S_2} - M{S_1} < k\lambda < M{S'_2} - M{S_1}\)
\( \Rightarrow 25 - 16 < 3k < 33,3 - 16 \Rightarrow 3 < k < 5,7 \Rightarrow k = 4;\,5\)
Có hai giá trị k thoả mãn.
Đáp án đúng: B
Câu 5:
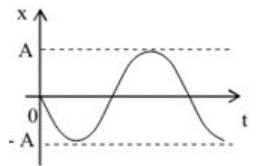
Đồ thị li độ của một vật cho ở hình vẽ bên, phương trình nào dưới đây là phương trình dao động của vật
 Xem đáp án
Xem đáp án
Lời giải
Tại vị trí ban đầu vật ở VTCB, vật đi theo chiều âm nên φ = π/2
=> Phương trình dao động: \(x = A\cos \left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right)\)
Đáp án đúng: A
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải
\(T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow T \sim \sqrt \ell \)
\( \Rightarrow \frac{{T'}}{T} = \sqrt {\frac{{\ell '}}{\ell }} = \sqrt 3 \Rightarrow T' = T\sqrt 3 = 2\sqrt 3 \left( s \right) \approx 3,46\left( s \right)\)
Đáp án đúng: C
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ dao động của con lắc khi thang máy đứng yên:
\(A = \frac{{{\ell _{max}} - {\ell _{\min }}}}{2} = \frac{{48 - 32}}{2} = 8\left( {cm} \right)\)
Độ biến dạng ở VTCB: \(\Delta \ell = \frac{{mg}}{k} = 0,16\left( m \right) = 16\left( {cm} \right)\)
Lại có: \({\ell _{max}} = {\ell _0} + \Delta \ell + A \Rightarrow {\ell _0} = 24\left( {cm} \right)\)
Tại thời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc a = g/10 thì con lắc chịu tác dụng của lực quán tính \({F_{qt}} = ma = 0,4.1 = 0,4\left( N \right)\)hướng lên.
Lực này sẽ gây ra biến dạng thêm cho vật đoạn: \(x = \frac{{{F_{qt}}}}{k} = \frac{{0,4}}{{25}} = 0,016\left( m \right) = 1,6\left( {cm} \right)\)
Vậy sau đó vật dao động với biên độ: 8 + 1,6 = 9,6 cm.
Đáp án đúng: DCâu 8:
 Xem đáp án
Xem đáp án
Lời giải
Dao động tổng hợp của hai dao động đó sẽ có biên độ bằng
\[{A_{th}} = \sqrt {{A^2} + {A^2} + 2A.A.\cos \frac{{2\pi }}{3}} = A\]
Đáp án đúng: B
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Hai quả cầu hút nhau nên chúng tích điện trái dấu.
Vì điện tích trái dấu nên:
\(\left| {{q_1}{q_2}} \right| = - {q_1}{q_2} = \frac{{F.{r^2}}}{{{{9.10}^9}}} = \frac{{16}}{3}{.10^{ - 12}} \Rightarrow {q_1}{q_2} = - \frac{{16}}{3}{.10^{ - 12}}\)(1)
Sau khi tiếp xúc \[q{'_1} = q{'_2} = \frac{{{q_1} + {q_2}}}{2}\] và cho chúng trở lại khoảng cách như cũ:
\[{\left( {\frac{{{q_1} + {q_2}}}{2}} \right)^2} = \frac{{F'{r^2}}}{{{{9.10}^9}}} = \frac{{16}}{3}{.10^{ - 12}} \Rightarrow {q_1} + {q_2} = \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}\left( 2 \right)\]
Từ (1) và (2) ta thấy q1 và q2 là nghiệm của các phương trình:
\(3{q^2} \pm \sqrt {192} {.10^{ - 6}}q - {16.10^{ - 12}} = 0\)
\( \Rightarrow \left\{ \begin{array}{l}{q_1} = {0,96.10^{ - 6}}C\\{q_2} = - {5,58.10^{ - 6}}C\end{array} \right.\)hoặc \(\left\{ \begin{array}{l}{q_2} = {0,96.10^{ - 6}}C\\{q_1} = - {5,58.10^{ - 6}}C\end{array} \right.\)
Hoặc \(\left\{ \begin{array}{l}{q_1} = - {0,96.10^{ - 6}}C\\{q_2} = {5,58.10^{ - 6}}C\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}{q_2} = - {0,96.10^{ - 6}}C\\{q_1} = {5,58.10^{ - 6}}C\end{array} \right.\)
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
+ Chu kì dao động điều hòa của con lắc lò xo không phụ thuộc vào biên độ dao động.
+ T’ = T/2 = 0,15 s.
Đáp án đúng: A
Câu 11:
 Xem đáp án
Xem đáp án
Lời giải
Lực đàn hồi tác dụng lên vật khi ở VTCB:
\({F_{dh}} = k\Delta {\ell _0} \Rightarrow k = \frac{{{F_{dh}}}}{{\Delta {\ell _0}}} = \frac{2}{{0,05}} = 40\left( {{\rm{N/m}}} \right)\)
Tần số góc của dao động: \(\omega = \sqrt {\frac{g}{{\Delta {\ell _0}}}} = 10\sqrt 2 \) rad/s
Lò xo giãn 2 cm, li độ của vật khi đó: x = 2 – 5 = –3 (cm)
Áp dụng công thức độc lập với thời gian tại thời điểm t = 0, ta có:
\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 5\left( {cm} \right)\)
Giá trị cực đại của lực đàn hồi tác dụng lên vật:
Fdhmax = k.(Δℓ + A) = 40.(0,05 + 0,05) = 4 (N).
Đáp án đúng: A
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ dao động tổng hợp: A = 10 cm => \[W = \frac{1}{2}m{\omega ^2}{A^2} = {5.10^{ - 3}}\,J\]
Đáp án đúng: ACâu 13:
 Xem đáp án
Xem đáp án
Lời giải
Lúc đầu vật ở biên âm x = -A
Vật qua li độ \(x = - \frac{A}{2}\)theo chiều dương lần đầu tiên tại \(\frac{T}{6}\)
Vật qua li độ - 2 cm theo chiều dương vào những thời điểm:
\(t = \frac{T}{6} + kT = \frac{{0,5}}{6} + k.0,5 = \frac{1}{{12}} + \frac{k}{2}\)
Đáp án đúng: A
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
Tại thời điểm ban đầu vật xuất phát từ VTCB đi theo chiều dương.
Chu kì dao động \(T = \frac{{2\pi }}{\omega } = 1\left( s \right)\)
Xét khoảng thời gian \(t = 12,375 = 12T + \frac{{3T}}{8}\)
Như vậy quãng đường đi được sẽ là s = s1 + s2
với s1 là quãng đường vật đi được trong thời gian 12T kể từ khi bắt đầu dao động, s2 là quãng đường vật đi được trong thời gian \(\frac{{3T}}{8}\) tiếp theo.
- Trong thời gian 12T, quãng đường vật đi được là s1 = 12.4A = 48A
- Trong thời gian \(\frac{{3T}}{8}\) tiếp theo, vật đi được quãng đường:
\({s_2} = A + \left( {A - \frac{{A\sqrt 2 }}{2}} \right) = 2A - \frac{{A\sqrt 2 }}{2}\)
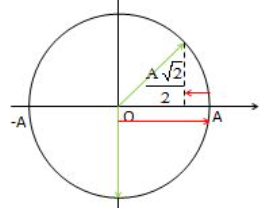
Vậy, tổng quãng đường đi được là: \(s = {s_1} + {s_2} = 48A + 2A - \frac{{A\sqrt 2 }}{2} = 50A - \frac{{A\sqrt 2 }}{2}\)
Thay số vào ta được s = 246,46 cm.
Đáp án đúng: B
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
\[{F_{kv\;max}} = \;k.A = \;m{\omega ^2}A = \;0,4\;N\]
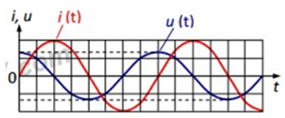
Đáp án đúng: B
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Với con lắc lò xo ta có: \(\omega = \sqrt {\frac{k}{m}} \Rightarrow 2\pi f = \sqrt {\frac{k}{m}} \Rightarrow k = 4{\pi ^2}{f^2}m = 800\left( {N/m} \right)\)
Đáp án đúng: A
Câu 17:
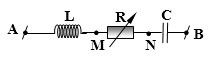
 Xem đáp án
Xem đáp án
Lời giải
Thời điểm ban đầu t = 0 vật qua VTCB theo chiều âm
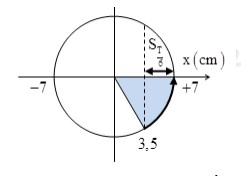
Vật có gia tốc bằng một nửa giá trị cực đại \( \Leftrightarrow - {\omega ^2}x = \frac{{{\omega ^2}A}}{2} \Rightarrow x = - \frac{A}{2}\)
Biểu diễn các thời điểm trên đường tròn lượng giác:
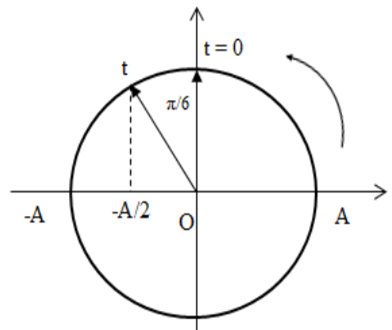
Góc quét là \(\alpha = \frac{\pi }{6} \Rightarrow t = \frac{\alpha }{\omega } = \frac{T}{{12}}\)
Đáp án đúng: ACâu 18:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ A = 2 cm = 0,02 m
\({F_x} = kx = 100x \le 1 \Rightarrow x \le 0,01\,\left( m \right) \Rightarrow x \le \frac{A}{2}\)\( \Rightarrow \Delta t = 4.\frac{T}{{12}} = \frac{T}{3}\)
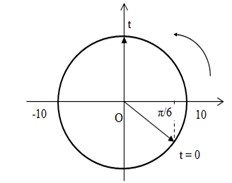
Đáp án đúng: B
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
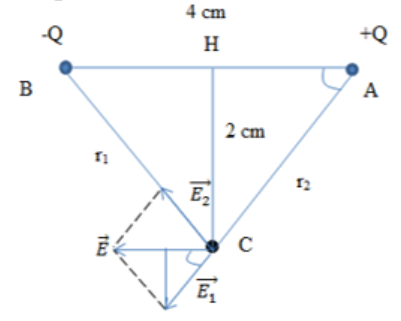
Ta có: \({r_1} = {r_2} = \sqrt {A{H^2} + A{C^2}} = 2\sqrt 2 \left( {cm} \right)\)
Vì \(\left| {{q_1}} \right| = \left| {{q_2}} \right|\) và \({r_1} = {r_2} \Rightarrow {E_1} = {E_2} = k\frac{{\left| {{q_1}} \right|}}{{r_1^2}} = {9.10^5}\left( {{\rm{V/m}}} \right)\)
Từ hình vẽ ta có: \(E = 2{E_1}\cos \alpha \)
Với \(\cos \alpha = \frac{{AH}}{{AC}} = \frac{2}{{2\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow E = 2{E_1}\frac{{\sqrt 2 }}{2} = {12,73.10^5}\left( {{\rm{V/m}}} \right)\)
Đáp án đúng: CCâu 20:
 Xem đáp án
Xem đáp án
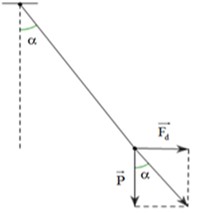
Lời giải
Ta có:
\(\left\{ \begin{array}{l}{v_{max}} = \omega A\\{a_{max}} = {\omega ^2}A\end{array} \right. \Rightarrow v_{max}^2 = {\omega ^2}{A^2} \Rightarrow \frac{{v_{max}^2}}{{{a_{max}}}} = A = 4\left( {cm} \right)\)
Đáp án đúng: B
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
+ Ta có: A = 20 cm; x = 10 cm; v = 20π\(\sqrt 3 \) cm/s.
+ Áp dụng công thức độc lập:
\(\omega = \sqrt {\frac{{{v^2}}}{{{A^2} - {x^2}}}} = 2\pi \left( {{\rm{rad/s}}} \right) \Rightarrow T = \frac{{2\pi }}{\omega } = 1\left( s \right)\)
Đáp án đúng: B
Câu 22:
 Xem đáp án
Xem đáp án
Lời giải
Người ta cho nước nhỏ đều đặn lên điểm O nằm trên mặt nước phẳng lặng với tốc độ 90 giọt trong 1 phút => Tần số sóng là \(f = \frac{{90}}{{60}} = 1,5\left( {Hz} \right)\)
Khoảng cách giữa hai vòng tròn liên tiếp là 1 bước sóng do đó
\(\lambda = \frac{v}{f} = \frac{{60}}{{1,5}} = 40\left( {cm} \right)\)
Đáp án đúng: CCâu 23:
 Xem đáp án
Xem đáp án
Lời giải
S1 và S2 cùng pha, tại trung điểm:\({d_1} - {d_2} = 0 = k\lambda \)
⇒ Điểm đó dao động cực đại.
Đáp án đúng: A
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Áp dụng công thức tính công của lực điện ta có:
\(A = qU = qEd \Rightarrow E = \frac{A}{{qd}} = 200\left( {{\rm{V/m}}} \right)\)
Đáp án đúng: BCâu 25:
 Xem đáp án
Xem đáp án
Lời giải
Phương pháp: Sử dụng lí thuyết về sự truyền sóng
+ Phao nhô lên 5 lần trong 20 s => 4T = 20 s => chu kì T = 5 s.
+ Khoảng cách giữa 2 đỉnh sóng liên tiếp λ = 2 m
=> Vận tốc truyền sóng v = λ/T = 2/5 = 0,4 m/s = 40 cm/s
Đáp án đúng: A
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
Ta có hình vẽ:
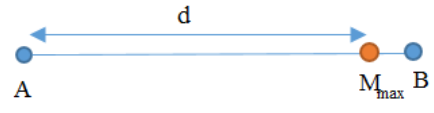
Do số vân giao thoa cực đại nhiều hơn số vân giao thoa cực tiểu và M là cực đại xa A nhất nên khoảng từ M đến B không có vân cực tiểu, do đó đoạn \[MB < \frac{\lambda }{4}\]
Tại B không phải là cực đại nên ta có:
\(d + \frac{\lambda }{4} > AB \Rightarrow \lambda > 4\left( {AB - d} \right) = 2,4\left( {cm} \right)\)\( \Rightarrow \frac{{AB}}{\lambda } < \frac{{12,6}}{{2,4}} = 5,25\)
Giả sử có 5 cực đại ở hai bên đường trung trực của AB, hay tại M là cực đại bậc 5 thì ta có: \(AM - BM = 5\lambda \Rightarrow \lambda = \frac{{AM - BM}}{5} = \frac{{12 - 0,6}}{5} = 2,28\left( {cm} \right)\)
Loại vì \(\lambda > 2,4\left( {cm} \right)\)
Vậy giả sử có 4 cực đại mỗi bên đường trung trực của AB, hay tại M là cực đại bậc 4 thì ta có: \(AM - BM = 4\lambda \Rightarrow \lambda = \frac{{AM - BM}}{4} = \frac{{12 - 0,6}}{4} = 2,85\left( {cm} \right)\)
Khi đó trên AB có 9 cực đại (k = ±4; ±3; ±2; ±1; 0)
Số cực tiểu trên BA là số giá trị k thỏa mãn
\( - \frac{{AB}}{\lambda } - \frac{1}{2} < k < \frac{{AB}}{\lambda } - \frac{1}{2} \Rightarrow - 4,9 < k < 3,9\)
Khi đó trên AB có 8 cực tiểu \(\left( {k = - 4; \pm 3; \pm 2; \pm 1;0} \right)\) thỏa mãn điều kiện đề bài.
Đáp án đúng: D
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải
Phương trình sóng u = 5cos(6πt - πx) (cm) (x tính bằng mét, t tính bằng giây)
Tần số \[f = \frac{\omega }{{2\pi }} = 3\,Hz\]
Ta có \[\pi x = \frac{{2\pi x}}{\lambda } \Rightarrow \lambda = 2\,m\]
Tốc độ truyền sóng: v = λ.f = 6 m/s
Đáp án đúng: DCâu 28:
 Xem đáp án
Xem đáp án
Lời giải
Ta có tốc độ trung bình của vật trong 1 chu kì: \({v_{tb}} = \frac{s}{t} = \frac{{4A}}{T} = \frac{{4A}}{{\frac{{2\pi }}{\omega }}} = \frac{{2A\omega }}{\pi }\)
Vận tốc tức thời: \(v \ge \frac{\pi }{4}{v_{tb}} = \frac{\pi }{4}.\frac{{2A\omega }}{\pi } \Rightarrow v \ge \frac{{A\omega }}{2} = \frac{{{v_{max}}}}{2}\)
Áp dụng công thức độc lập với thời gian, ta có: \( - \frac{{A\sqrt 3 }}{2} \le x \le \frac{{A\sqrt 3 }}{2}\)
Biểu diễn trên VTLG, ta có:
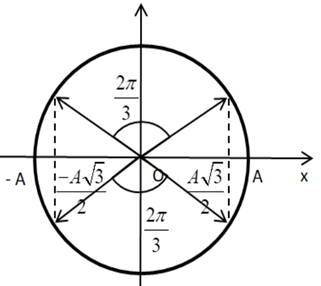
Từ VTLG, ta thấy khoảng thời gian vật có độ lớn vận tốc tức thời không nhỏ hơn π/4 lần tốc độ trung bình trong 1 chu kỳ là: \(\Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{2T}}{3}\)
Đáp án đúng: CCâu 29:
 Xem đáp án
Xem đáp án
Lời giải
Khi có cộng hưởng, chu kì dao động đó chính là chu kì dao động riêng của hệ:
\(T = 2\pi \sqrt {\frac{\ell }{g}} = 2\pi \sqrt {\frac{{0,5}}{{10}}} = 1,405\left( s \right)\)
Đáp án đúng: C
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
Trong dao động điều hoà, gia tốc biến đổi sớm pha \(\frac{\pi }{2}\) so với vận tốc.
Đáp án đúng: B
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Khi đặt trong không khí: \[\left\{ \begin{array}{l}F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_2}} \right|\end{array} \right. \Rightarrow \left| {{q_1}} \right| = \left| {{q_2}} \right| = \sqrt {\frac{{F.{r^2}}}{k}} = {4.10^{ - 6}}\left( C \right)\]
Khi đặt trong dầu: \({F_\varepsilon } = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} \Rightarrow \varepsilon = 2,25\)
Đáp án đúng: B
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
Một con lắc lò xo dao động điều hòa thì vật có tốc độ cực đại khi vật đi qua vị trí cân bằng.
Đáp án đúng: CCâu 33:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì: \(T = 0,1\left( s \right)\)
Thời gian vật đi đoạn đường ngắn nhất từ vị trí cân bằng đến vị trí có li độ x = 3 cm là \(\Delta t = \frac{T}{{12}} = \frac{1}{{120}}\left( s \right)\)
Vận tốc trung bình của vật khi đi đoạn đường ngắn nhất từ vị trí cân bằng đến vị trí có li độ x = 3 cm là
\(\overline v = \frac{{{x_{sau}} - {x_{truoc}}}}{{\Delta t}} = \frac{{3 - 0}}{{\frac{1}{{120}}}} = 360\left( {{\rm{cm/s}}} \right) = 3,6\left( {{\rm{m/s}}} \right)\)
Đáp án đúng: BCâu 34:
 Xem đáp án
Xem đáp án
Lời giải
Ta có, q1.q2 < 0 => lực tương tác giữa hai điện tích là lực hút.
Theo định luật Cu-lông, ta có: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon .{r^2}}} = 45\left( N \right)\)
Đáp án đúng: A
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)
\(T' = 2\pi \sqrt {\frac{{m'}}{{k'}}} = 2\pi \sqrt {\frac{{\frac{m}{2}}}{{2k}}} = \frac{T}{2}\)
Đáp án đúng: D
Câu 36:
 Xem đáp án
Xem đáp án
Lời giải
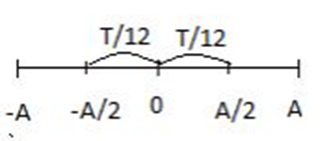
Vì hòn bi chuyển động trên một cung tròn dài 4 cm nên biên độ dao động A = 4 cm
=> Thời gian để hòn bi đi được 2 cm kể từ VTCB là t = T/12 = 0,25 s
Đáp án đúng: A
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
Trrong 10 s thực hiện được 20 dao động
⇒ Trong 1 s thực hiện được 2 dao động
⇒ \(f = 2 \Rightarrow \omega = 2\pi f = 4\pi \left( {{\rm{rad/s}}} \right)\)
\( \Rightarrow L = 10\left( {cm} \right) \Rightarrow A = 5\left( {cm} \right)\)
Tại t = 0 vật qua VTCB theo chiều dương \(\varphi = - \frac{\pi }{2}\)\( \Rightarrow x = 5\cos \left( {4\pi t - \frac{\pi }{2}} \right)\)
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Tần số dao động riêng của con lắc lò xo: \[f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = 5\,Hz\]
Khi tần số ngoại lực < 5 Hz thì khi tăng tần số biên độ dao động cưỡng bức tăng lên.
Đáp án đúng: B
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
* Tần số góc của CLLX: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,1}}} = 10\sqrt 2 \left( {{\rm{rad/s}}} \right)\)
* Kéo quả cầu thẳng đứng xuống dưới vị trí cân bằng một đoạn \(2\sqrt 2 \) cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là \(0,2\sqrt 2 \left( {{\rm{m/s}}} \right) = 20\sqrt 2 \left( {{\rm{cm/s}}} \right)\)
⇒ Biên độ \(A = \sqrt {{x^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = 4\left( {cm} \right)\)
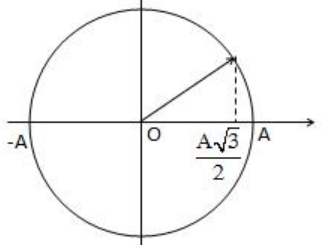
* Gốc thời gian là lúc thả quả cầu, nghĩa là lúc vật có li độ \(x = 2\sqrt 3 \) cm và chuyển động theo chiều âm(vì chiều dương hướng xuống)
=> Pha ban đầu φ = π/6 rad
Vậy, phương trình dao động của vật là:
\(x = 4\cos \left( {10\sqrt 2 t + \frac{\pi }{6}} \right)\left( {cm} \right) = 4\sin \left( {10\sqrt 2 t + \frac{{2\pi }}{3}} \right)\) cm.
Đáp án đúng: B
Câu 40:
 Xem đáp án
Xem đáp án
Lời giải
\(s = 6{t^2} - {t^3} > 0 \Rightarrow v\left( t \right) = s'\left( t \right) = 12t - 3{t^2}\)
Ta có: \(v'\left( t \right) = 12 - 6t,v'\left( t \right) = 0 \Rightarrow t = 2\)
Hàm số v(t) đồng biến trên khoảng (0; 2) và nghịch biến trên khoảng (2; +∞).
Do đó maxv(t) = v(2) = 12 (m/s)
Vậy vận tốc đạt giá trị lớn nhất khi \(t = 2\).
Đáp án đúng: C
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Kéo con lắc trên cung độ dài 5 cm rồi thả nhẹ => So = 5 cm
\(\omega = \sqrt {\frac{g}{\ell }} = \) 2 rad/s
Chiều dương hướng từ vị trí cân bằng tới góc lệch ban đầu
=> s = So => \(\varphi \) = 0 => s = 5cos(2t) = 5sin( 2t + π/2)(cm).
Đáp án đúng: D
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
\(\omega = \frac{{2\pi }}{T} = \pi \left( {rad/s} \right)\)
\(\omega A = 31,4 \Rightarrow A = 10\)
Tại t = 0, x = 5 > 0 và đi theo chiều âm
\(\varphi = \arccos \frac{5}{{10}} = \frac{\pi }{3}\) => x = 10cos(πt + π /3)(cm).
Đáp án đúng: ACâu 43:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì dao động: T = 2s
Ta có: ∆t = 1,5s = 1s + 0,5s = T/2 + T/4 => Smax = 2A + SmaxT/4
=> Góc quét được trong khoảng thời gian T/4 là π/2.
Quãng đường vật đi được trong \[\frac{1}{2}\] chu kì là 2A.
Vật có tốc độ cực đại khi qua vị trí cân bằng. Trong cùng một khoảng thời gian vật đi được quãng đường lớn nhất khi đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có:
\( \Rightarrow {S_{max\frac{T}{4}}} = \frac{5}{{\sqrt 2 }} + \frac{5}{{\sqrt 2 }} = 5\sqrt 2 \) cm
\( \Rightarrow {S_{max}} = 2A + {S_{max\frac{T}{4}}} = 2.5 + 5\sqrt 2 = 17,07\left( {cm} \right)\)
Đáp án đúng: B
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải
Ban đầy mạch RL có u và i lệch pha \[\frac{\pi }{6}\] nên \[\tan \frac{\pi }{6} = \frac{{{Z_L}}}{R} \Rightarrow {Z_L} = \frac{{100}}{{\sqrt 3 }}\,\Omega \]
Để u và i cùng pha ⇒ mạch gồm đủ 3 phần tử R, L, C và mạch xảy ra cộng hưởng.
⇒ Nối tiếp với mạch một tụ điện có ZC = \(\frac{{100}}{{\sqrt 3 }}\Omega \).
Đáp án đúng: ACâu 45:
 Xem đáp án
Xem đáp án
Lời giải
Khi vật nặng đi qua vị trí cân bằng thì trọng lực tác dụng lên nó không cân bằng với lực căng dây.
Đáp án đúng: D
Câu 46:
 Xem đáp án
Xem đáp án
Lời giải
Mỗi phút vật thực hiện được 120 dao động \( \Rightarrow T = \frac{{60}}{{120}} = 0,5\left( s \right)\)
Động năng bằng nửa cơ năng tức là động năng bằng thế năng.
Thời gian 2 lần liên tiếp để động năng bằng thế năng là \(\Delta t = \frac{T}{4} = 0,125\left( s \right)\)
Đáp án đúng: C
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
Fđhmax = k.( ∆l + A)
Fđhmin = k(∆l – A)
\(\Delta \ell = \frac{g}{{{\omega ^2}}} = \frac{g}{{{{\left( {2\pi f} \right)}^2}}} = 0,25\left( m \right)\)
\(\frac{{{F_{dh\min }}}}{{{F_{dh\max }}}} = \frac{{k\left( {\Delta \ell - A} \right)}}{{k\left( {\Delta \ell + A} \right)}} = \frac{3}{7}\)
Đáp án đúng: DCâu 48:
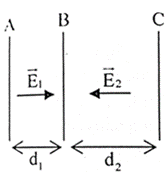
 Xem đáp án
Xem đáp án
Lời giải
Mốc điện thế tại A: \({V_A} = 0\)
\({U_1} = {E_1}{d_1} = {V_B} - {V_A} \Rightarrow {V_B} = {E_1}{d_1} = 2000\left( V \right)\)
\({U_2} = {E_2}{d_2} = {V_B} - {V_C} \Rightarrow {V_C} = {E_2}{d_2} = - 2000\left( V \right)\)
Đáp án đúng: B
Câu 49:
 Xem đáp án
Xem đáp án
Lời giải
Áp dụng công thức tính cường độ điện trường ta xác định được cường độ điện trường tại A, B, M như sau:
\(\left\{ \begin{array}{l}{E_A} = k\frac{{\left| q \right|}}{{r_A^2}} \Rightarrow {r_A} = \sqrt {\frac{{k\left| q \right|}}{{{E_A}}}} \\{E_B} = k\frac{{\left| q \right|}}{{r_B^2}} \Rightarrow {r_B} = \sqrt {\frac{{k\left| q \right|}}{{{E_B}}}} \\{E_M} = k\frac{{\left| q \right|}}{{r_M^2}} \Rightarrow {r_M} = \sqrt {\frac{{k\left| q \right|}}{{{E_M}}}} \end{array} \right.\)
Vì điểm M là trung điểm của A và B nên \({r_M} = \frac{{{r_A} + {r_B}}}{2}\)
Ta có: \(\sqrt {\frac{{k\left| q \right|}}{{{E_M}}}} = \frac{{\sqrt {\frac{{k\left| q \right|}}{{{E_A}}}} + \sqrt {\frac{{k\left| q \right|}}{{{E_B}}}} }}{2} \Rightarrow \sqrt {\frac{1}{{{E_M}}}} = \frac{{\sqrt {\frac{1}{{{E_A}}}} + \sqrt {\frac{1}{{{E_B}}}} }}{2} \Rightarrow {E_M} = 34,02\left( {{\rm{V/m}}} \right)\)
Đáp án đúng: A
Câu 50:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ dao động tổng hợp được xác định bởi
\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi \)
Do \(\left| {\cos \Delta \varphi } \right| \le 1\) nên biên độ dao động cực đại khi |cos Δφ| = 1, suy ra:
\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2} \Rightarrow {A^2} = {\left( {{A_1} + {A_2}} \right)^2} \Rightarrow A = {A_1} + {A_2}\)
Đáp án đúng: ACâu 51:
 Xem đáp án
Xem đáp án
Lời giải
Chu kỳ dao động là thời gian vật thực hiện 1 dao động toàn phần. Vậy để đo chu kỳ dao động ta cần dùng đồng hồ bấm giây.
Đáp án đúng: A
Câu 52:
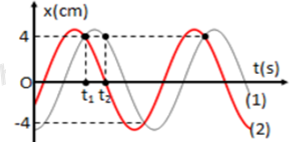
 Xem đáp án
Xem đáp án
Lời giải
Từ đồ thị ta có:
+ Tại thời điểm t1: x2 = 4 cm↓ và x1 = 4 cm↑
+ Tại thời điểm t2: x2 = 0 cm↓ và x1 = 4 cm↓
Gọi A và φ là biên độ dao động và độ lệch pha của hai dao động thành phần.
Biểu diễn trên VTLG ta có:
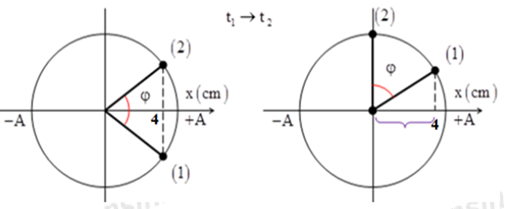
Từ VTLG, ta có: \(\left\{ \begin{array}{l}\cos \frac{\varphi }{2} = \frac{4}{A}\\\sin \varphi = \frac{4}{A}\end{array} \right. \Rightarrow \cos \frac{\varphi }{2} = \sin \varphi \)
\( \Leftrightarrow \cos \frac{\varphi }{2} = \cos \left( {\varphi - \frac{\pi }{2}} \right) \Rightarrow \varphi = \frac{\pi }{3} \Rightarrow A = \frac{8}{{\sqrt 3 }}\left( {cm} \right)\)
Biên độ dao động tổng hợp hai dao động thành phần là:
\({A_{th}} = \sqrt {{A^2} + {A^2} + 2.A.A.\cos \varphi } = 8\left( {cm} \right) = 0,08\left( m \right)\)
Ta có: \(\varphi = \frac{\pi }{3} \Rightarrow {t_{1 \to 2}} = \frac{\varphi }{\omega } = \frac{{\frac{\pi }{3}}}{{\frac{{2\pi }}{T}}} = \frac{T}{6}\)
\({t_2} - {t_1} = \frac{T}{6} = \frac{1}{3}\left( s \right) \Rightarrow T = 2\left( s \right)\)
Cơ năng của chất điểm có giá trị bằng: \[{\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = {6,4.10^{ - 3}}\left( J \right) = 6,4\left( {mJ} \right)\]
Đáp án đúng: D
Câu 53:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({L_2} - {L_1} = 10\log \frac{{{I_2}}}{{{I_1}}} = 10\log \frac{{10{I_1}}}{{{I_1}}} = 10\left( {dB} \right)\)
Đáp án đúng: A
Câu 54:
Một điện tích điểm q = -4.10-8C di chuyển dọc theo chu vi của một tam giác MNP, vuông tại P, trong điện trường đều có cường độ 200 V/m. Cạnh MN = 10 cm, MN cùng phương cùng chiều với \(\vec E\). Cho NP = 8 cm. Môi trường là không khí. Tính công của lực điện trong các dịch chuyển sau của q:
a, từ M đến N.
b, từ N đến P.
c, từ P đến M.
d, theo đường kín MNPM.
 Xem đáp án
Xem đáp án
Lời giải
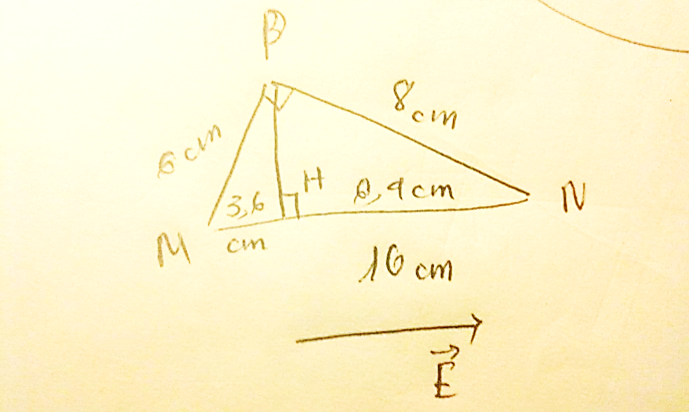
Hình chiếu của P xuống MN là H
Hệ thức lượng trong tam giác vuông:
\(P{N^2} = NH.MN \Rightarrow HN = 6,4\left( {cm} \right)\)
\(MN = MH + HN \Rightarrow HM = 3,6\left( {cm} \right)\)
Công của lực điện: \(A = qEd\)
\(A > 0\) khi điện tích chuyển động ngược chiều \(\vec E\) (do điện tích âm)
\(A < 0\) khi điện tích chuyển động cùng chiều \(\vec E\)
a. \({A_{MN}} = q.E.MN = - {4.10^{ - 8}}.200.0,1 = - {8.10^{ - 7}}\left( J \right)\)
B. \({A_{NP}} = q.E.NH = {4.10^{ - 8}}.200.0,064 = {5,12.10^{ - 7}}\left( J \right)\) (do ngược chiều điện trường)
c. \({A_{PM}} = q.E.MH = {4.10^{ - 8}}.200.0,036 = {2,88.10^{ - 7}}\left( J \right)\)(do ngược chiều điện trường)
d. A = 0.
Câu 55:
 Xem đáp án
Xem đáp án
Lời giải
+ Các phần tử giữa hai nút sóng liền kề nằm trên cùng một bó sóng.
+ Các phân tử trên cùng 1 bó sóng luôn dao động cùng pha.
Đáp án đúng: D
Câu 56:
 Xem đáp án
Xem đáp án
Lời giải
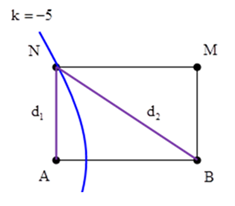
Số điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn: \(N = 2.\left[ {\frac{{AB}}{\lambda }} \right] + 1 = 11\)
+ Để số điểm dao động với biên độ cực đại trên MN là nhiều nhất thì N phải nằm trên hypebol cực đại ứng với \(k = - 5\)
+ N đối xứng với M nên N nằm trên cực đại bậc 5, ta có \({d_2} - {d_1} = 5\lambda = 40\left( {cm} \right)\)
Mặt khác: \({d_2} = \sqrt {d_1^2 + {{44}^2}} \Rightarrow \sqrt {d_1^2 + {{44}^2}} - {d_1} = 40 \Rightarrow {d_1} = 4,2\left( {cm} \right)\)
Diện tích của hình chữ nhật:
\(S = AB.AN = 44.4,2 = 184,8\left( {c{m^2}} \right)\)
Đáp án đúng: B
Câu 57:
 Xem đáp án
Xem đáp án
Lời giải
Do q1.q2 > 0 nên vị trí điểm M có cường độ điện trường tổng hợp bằng 0 nằm trong khoảng giữa q1 và q2.
Gọi x là khoảng cách từ vị trí điểm M đến điện tích q1
Ta có, tại M cường độ điện trường tổng hợp bằng 0, nên ta có:
\({\vec E_1} + {\vec E_2} = 0 \Rightarrow {E_1} = {E_2} \Rightarrow k\frac{{{q_1}}}{{{x^2}}} = k\frac{{{q_2}}}{{{{\left( {a - x} \right)}^2}}} \Rightarrow a - x = 2x \Rightarrow x = \frac{a}{3} = 3\left( {cm} \right) = 0,03\left( m \right)\)
Điện thế tại M: \({V_M} = {V_{1M}} + {V_{2M}} = k\frac{{{q_1}}}{x} + k\frac{{{q_2}}}{{a - x}} = 900\left( V \right)\)
Đáp án đúng: C
Câu 58:
 Xem đáp án
Xem đáp án
Lời giải
Tần số góc của dao động: \(\omega = \sqrt {\frac{k}{m}} = 10\left( {rad/s} \right)\)
Độ biến dạng của lò xo tại VTCB: \(\Delta {\ell _o} = \frac{{mg}}{k} = 10\left( {cm} \right)\)
Nâng vật đến vị trí lò xo không biến dạng rồi thả nhẹ ⇒ Vật sẽ dao động với biên độ \( \Rightarrow A = \Delta {\ell _0} = 10\left( {cm} \right)\)
⇒ Ban đầu vật ở vị trí biên âm
⇒ \({\varphi _0} = \pi \Rightarrow x = 10\cos \left( {10t + \pi } \right)\)cm
Đáp án đúng: B
Câu 59:
 Xem đáp án
Xem đáp án
Lời giải
Bước sóng: λ = v/f = 2 cm
Số điểm dao động với biện độ cực đại trên đoạn thẳng AB bằng số giá trị k nguyên thoả mãn:
\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow - \frac{{16}}{2} < k < \frac{{16}}{2} \Leftrightarrow - 8 < k < 8\)
⇒ Có 15 giá trị của k nguyên thỏa mãn
Vậy có 15 điểm dao động với biên độ cực đại trên đoạn thẳng AB.
Đáp án đúng: B
Câu 60:
 Xem đáp án
Xem đáp án
Lời giải
\(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Để hệ số công suất cosφ = 0 thì R = 0
Đáp án đúng: C
Câu 61:
 Xem đáp án
Xem đáp án
Lời giải
Ta có, khi đưa 2 cực lại gần nhau:
+ 2 cực cùng tên thì đẩy nhau
+ 2 cực khác tên thì hút nhau
Đáp án đúng: B
Câu 62:
 Xem đáp án
Xem đáp án
Lời giải
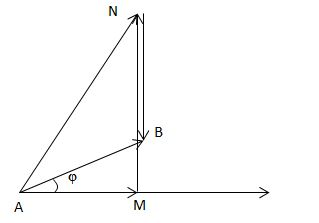
Ta vẽ được giản đồ véc tơ như sau:
Trong tam giác vuông MAB có: \(\widehat {MBA} + \varphi = {90^0} \Rightarrow \cos \varphi = \sin \widehat {MBA} = 0,8\)
Thấy rằng: \(\widehat {MBA} + \widehat {ABN} = {180^0} \Rightarrow \sin \widehat {ABN} = \sin \widehat {MBA} = 0,8\)
Do đó, \(\cos \widehat {ABN} = \pm \sqrt {1 - {{\sin }^2}\widehat {ABN}} = \pm 0,6\)
Vì \(\widehat {ABN}\) là góc tù nên cos\(\widehat {ABN}\)= -0,6
Trong tam giác ABN ta có: \(A{N^2} = A{B^2} + B{N^2} - 2AB.BN.\cos \widehat {ABN}\)
Tức là: \(U_{AN}^2 = U_{AB}^2 + U_{NB}^2 - 2{U_{AB}}.{U_{NB}}.\cos \widehat {ABN}\)
Thay số vào ta được: UAN = 400 V
Đáp án đúng: D
Câu 63:
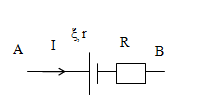
 Xem đáp án
Xem đáp án
Lời giải
Hiệu điện thế giữa hai điểm A và B được tính theo công thức:
\({U_{AB}} = E + I.\left( {R + r} \right)\) (vì chiều dòng điện đi vào cực dương của nguồn và đi từ A đến B)
Đáp án đúng: A
Câu 64:
 Xem đáp án
Xem đáp án
Lời giải
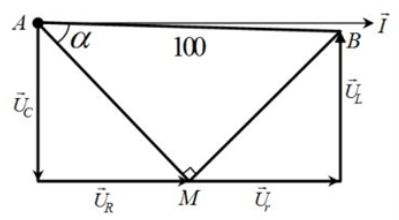
Vì \({\vec U_{AM}}\)trễ pha hơn \(\vec I\) góc \(\frac{\pi }{6}\) còn \({\vec U_{MB}}\) sớm pha hơn\(\vec I\) góc \(\frac{\pi }{3}\)
Nên \({\vec U_{AM}} \bot {\vec U_{MB}}\) hay \(\Delta AMB\) vuông tại M. Từ đó suy ra \({\vec U_{AM}}\) trễ pha hơn \({\vec U_{AB}}\) một góc \(\alpha \)sao cho AM = AB.cos\(\alpha \)
Ta nhận thấy chỉ có đáp án A thỏa mãn điều này.
Đáp án đúng: ACâu 65:
 Xem đáp án
Xem đáp án
Lời giải
Mạch R, L, C có điện áp và cường độ dòng điện lệch pha nhau một góc khác 900 thì đoạn mạch không thể là L nối tiếp C.
Đáp án đúng: C
Câu 66:
 Xem đáp án
Xem đáp án
Lời giải
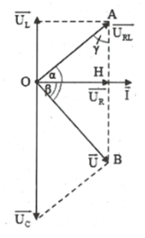
Từ giản đồ vecto, ta thấy: Trong tam giác vuông AOB luôn có: \(U_R^2 = {U_L}\left( {{U_C} - {U_L}} \right)\)
Đáp án đúng: ACâu 67:
 Xem đáp án
Xem đáp án
Lời giải
Mạch cộng hưởng thì ZL = Zc =>Z = R
Khi tăng dần tần số dòng điện và giữ nguyên các thông số của mạch thì ZL tăng Zc giảm => Z tăng =>cos\(\varphi \)=R/Z giảm và I giảm => A, B, D đúng
Vì Zc và I giảm => Uc =I.Zc cũng giảm => C sai
Kết luận không đúng là C
Đáp án đúng: C
Câu 68:
 Xem đáp án
Xem đáp án
Lời giải
Pha ban đầu của dao động: \(\varphi = - \pi \)
Chu kì dao động của vật: \(T = \frac{{2\pi }}{\omega } = 1\left( s \right)\)
Tại thời điểm \(t = \frac{8}{3}\left( s \right)\), ta có: \(t = \frac{{8T}}{3} = 2T + \frac{{2T}}{3}\)
Trong khoảng thời gian \(\frac{{2T}}{3}\), vật quay được góc: \(\Delta \varphi = \omega \Delta t = \frac{{2\pi }}{T}.\frac{{2T}}{3} = \frac{{4\pi }}{3}\left( {rad} \right)\)
Biểu diễn trên VTLG ta có:
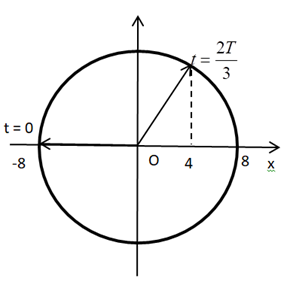
Từ VTLG, ta thấy quãng đường vật đi được là: \(S = 2.4.8 + 2.8 + \left( {8 - 4} \right) = 84\left( {cm} \right)\)
Đáp án đúng: C
Câu 69:
 Xem đáp án
Xem đáp án
Lời giải
Tổng trở của mạch: \(Z = \frac{U}{I} = \frac{{50}}{2} = 25\Omega \)
Ta có: \(\cos \frac{\pi }{6} = \frac{R}{Z} \Rightarrow R = 12,5\sqrt 3 \Omega \)
Đáp án đúng: CCâu 70:
 Xem đáp án
Xem đáp án
Lời giải
Ta có N1 > N2 => U1 > U2 => Máy hạ áp
Đáp án đúng: C
Câu 71:
 Xem đáp án
Xem đáp án
Lời giải
Để mạch xảy ra cộng hưởng:
\(\omega = \frac{1}{{\sqrt {LC} }} = 2\pi f \Rightarrow C = {5.10^{ - 5}}\left( F \right)\)
Câu 72:
 Xem đáp án
Xem đáp án
Lời giải
Để \({P_{Rm{\rm{ax}}}} \Rightarrow R = \left| {{Z_L} - {Z_C}} \right| \Rightarrow Z = R\sqrt 2 \)
Hệ số công suất: \(\cos \varphi = \frac{R}{Z} = \frac{{\sqrt 2 }}{2}\)
Đáp án đúng: C
Câu 73:
 Xem đáp án
Xem đáp án
Lời giải
Mạch chỉ có tụ điện nên u và i vuông pha ta áp dụng công thức độc lập thời gian:
\( \Rightarrow {\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1 \Rightarrow {\left( {\frac{u}{U}} \right)^2} + {\left( {\frac{i}{I}} \right)^2} = 2\)
Đáp án đúng: C
Câu 74:
 Xem đáp án
Xem đáp án
Lời giải
\(\sin \theta = \frac{1}{n}\)
\( \Rightarrow {\theta _{do}} > {\theta _{cam}} > {\theta _{vang}} > {\theta _{cham}} > {\theta _{tim}}\)
→ Màu vàng đi là là mặt nước( bắt đầu xảy ra hiện tượng phản xạ toàn phần) thì màu chàm và tím đã phản xạ hoàn toàn rồi → chỉ còn tia đỏ và tia cam ló ra không khí
Đáp án đúng: C
Câu 75:
 Xem đáp án
Xem đáp án
Lời giải
Khoảng thời gian giữa hai lần liên tiếp cường độ dòng diện bằng 0 là một nửa chu kỳ
Ta có: \(T = \frac{1}{f} = \frac{1}{{50}}\left( s \right) \Rightarrow \frac{T}{2} = \frac{1}{{2f}} = \frac{1}{{100}}\left( s \right)\)
Đáp án đúng: C
Câu 76:
 Xem đáp án
Xem đáp án
Lời giải
Để điện áp giữa hai đầu đoạn mạch cùng pha với điện áp giữa hai đầu điện trở R hay u cùng pha với i thì có cộng hưởng điện.
\( \Rightarrow {Z_C} = {Z_L} \Rightarrow C = \frac{{{{10}^{ - 3}}}}{\pi }\left( F \right)\)
Đáp án đúng: ACâu 77:
 Xem đáp án
Xem đáp án
Lời giải
Công suất tiêu thụ của mạch:
\(P = UI.\cos \varphi = 10.3.\cos \left( {\frac{{ - \pi }}{4} - \frac{\pi }{{12}}} \right) = 15\left( {\rm{W}} \right)\)
Đáp án đúng: A
Câu 78:
 Xem đáp án
Xem đáp án
Lời giải
Bước sóng: \(\lambda = 2\pi \sqrt {LC} = 25,289\left( m \right)\)
⇒ Đây là sóng ngắn.
Đáp án đúng: D
Câu 79:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({Z_C} = \frac{1}{{C\omega }} = 100\,\,\Omega ;{Z_L} = L\omega = 200\,\,\Omega \)
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = 100\sqrt 2 \Omega \)
Cường độ dòng điện hiệu dụng: \(I = \frac{U}{Z} = \frac{{200:\sqrt 2 }}{{100\sqrt 2 }} = 1\left( A \right)\)
Đáp án đúng: CCâu 80:
 Xem đáp án
Xem đáp án
Lời giải
Tác dụng của tụ điện đối với dòng điện xoay chiều là gây dung kháng nhỏ nếu tần số dòng điện lớn.\(\left( {{Z_C} = \frac{1}{{C\omega }} = \frac{1}{{C.2\pi f}} \Rightarrow {Z_C} \sim \frac{1}{f}} \right)\)
Đáp án đúng: A
Câu 81:
 Xem đáp án
Xem đáp án
Lời giải
Để thiết bị hoạt động tốt nhất thì giá trị định mức của thiết bị là: \(U = \frac{{{U_0}}}{{\sqrt 2 }} = 100\left( V \right)\)
Đáp án đúng: ACâu 82:
 Xem đáp án
Xem đáp án
Lời giải
Tần số góc: \(\omega = \sqrt {\frac{g}{\ell }} = \sqrt {\frac{{10}}{{{{40.10}^{ - 2}}}}} = 5\left( {{\rm{rad/s}}} \right)\)
Vận tốc của vật khi qua VTCB: \({v_{max}} = \omega {\alpha _0}\ell = 5.0,1.0,4 = 0,2\left( {m/s} \right) = 20\left( {{\rm{cm/s}}} \right)\)
Đáp án đúng: ACâu 83:
 Xem đáp án
Xem đáp án
Lời giải
Công thức tính điện dung của tụ điện phẳng: \(C = \frac{{\varepsilon .S}}{{4k\pi d}}\)
Khi tăng khoảng cách d giữa hai bản tụ lên 2 lần thì điện dung của tụ giảm đi 2 lần.
Đáp án đúng: C
Câu 84:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì dao động của chất điểm: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1\left( s \right)\)
Đáp án đúng: A
Câu 85:
 Xem đáp án
Xem đáp án
Lời giải
Chu kì dao động của vật: \(T = \frac{{60}}{{30}} = 2\left( s \right)\)
Quãng đường mà vật di chuyển trong 8 s, tương đương với 4T
\( \Rightarrow 4.4A = 64 \Rightarrow A = 4\left( {cm} \right)\)
Đáp án đúng: CCâu 86:
 Xem đáp án
Xem đáp án
Lời giải
Sử dụng tích phân: \(q = \int\limits_0^{\frac{T}{2}} {idt = } \int\limits_0^{\frac{T}{2}} {{I_0}\cos \left( {\omega t - \frac{\pi }{2}} \right)dt = } \frac{{2{I_0}}}{\omega }\)
Đáp án đúng: ACâu 87:
 Xem đáp án
Xem đáp án
Lời giải
Để nước sóng mạnh nhất thì khi đó phải xảy ra hiện tượng cộng hưởng.
Khi đó chu kì dao động riêng của nước và xô bằng chu kì bước chân của người sách:
\( \Rightarrow v = \frac{s}{T} = \frac{{0,5}}{1} = 0,5\left( {{\rm{m/s}}} \right)\)
Đáp án đúng: B
Câu 88:
 Xem đáp án
Xem đáp án
Lời giải
Bước sóng là: \(\lambda = \frac{v}{f} = \frac{{360}}{{300}} = 1,2\left( {cm} \right)\)
Biên độ dao động cực đại của phần tử môi trường là: A = 2a = 2.1 = 2 (cm)
Phần tử chất lỏng tại M dao động với biên độ 1 cm
\({A_M} = \frac{A}{2} \Rightarrow 2a\left| {\cos \frac{{\pi \left( {{d_2} - {d_1}} \right)}}{\lambda }} \right| = a\)\( \Rightarrow \cos \frac{{\pi \left( {{d_2} - {d_1}} \right)}}{\lambda } = \pm \frac{1}{2}\)
\( \Rightarrow \left[ \begin{array}{l}\frac{{\pi \left( {{d_2} - {d_1}} \right)}}{\lambda } = \frac{\pi }{3} + k\pi \\\frac{{\pi \left( {{d_2} - {d_1}} \right)}}{\lambda } = - \frac{\pi }{3} + k\pi \end{array} \right. \Rightarrow \left[ \begin{array}{l}\frac{{\left( {{d_2} - {d_1}} \right)}}{\lambda } = \frac{1}{3} + k\\\frac{{\left( {{d_2} - {d_1}} \right)}}{\lambda } = - \frac{1}{3} + k\end{array} \right.\)
Để M nằm trên S1S2: \( \Rightarrow - {S_1}{S_2} \le d{ & _2} - {d_1} \le {S_1}{S_2}\)
\( \Rightarrow \left[ \begin{array}{l} - 7,83 \le k \le 7,17\\ - 7,17 \le k \le 7,83\end{array} \right. \Rightarrow \left[ \begin{array}{l}k = - 7; - 6;...;6;7\\k = - 7; - 6;...;6;7\end{array} \right.\)
Vậy có tất cả 30 điểm dao động với biên độ a trên đoạn S1S2
Đáp án đúng: DCâu 89:
 Xem đáp án
Xem đáp án
Lời giải
Áp dụng công thức: \(v = \frac{s}{t} = \frac{{40}}{7} = 5,71\left( {{\rm{m/s}}} \right)\)
Đáp án đúng: B
Câu 90:
 Xem đáp án
Xem đáp án
Lời giải
+ Biên độ dao động tổng hợp được xác định bởi
\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi \Rightarrow {9^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {\frac{{ - 5\pi }}{6}} \right)\left( 1 \right)\)
Đạo hàm hai vế theo biến A1, ta thu được:
\[0 = 2{A_1} + 2{A_2}{A'_2} + 2{A_2}\cos \left( {\frac{{ - 5\pi }}{6}} \right) + 2{A_1}\cos \left( {\frac{{ - 5\pi }}{6}} \right){A'_2}\]
Để A2 cực đại tại \({A'_2} = 0 \Leftrightarrow {A_2} = - \frac{{{A_1}}}{{\cos \left( { - \frac{{5\pi }}{6}} \right)}} = \frac{{2{A_1}}}{{\sqrt 3 }}\)
Thay kết quả vào (1) ta được: \({A_1} = 9\sqrt 3 \left( {cm} \right)\)
Đáp án đúng: B
Câu 91:
 Xem đáp án
Xem đáp án
Lời giải
Độ biến dạng của lò xo tại vị trí cân bằng: \(\Delta {\ell _0} = \frac{{mg}}{k} = \frac{{{{600.10}^{ - 3}}.10}}{{100}} = 6\left( {cm} \right)\)
Lực đàn hồi của lò xo tác dụng lên vật có độ lớn: \({F_{dh\min }} = k\left( {\Delta {\ell _0} - A} \right) = 2\left( N \right)\)
Đáp án đúng: A
Câu 92:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ dao động đạt cực đại khi tần số dao động riêng bằng tần số của ngoại lực:
\( \Rightarrow f = \frac{\omega }{{2\pi }} = 2\pi \Rightarrow \omega = 40 \Rightarrow \sqrt {\frac{k}{m}} = 40 \Rightarrow m = 0,1\left( {kg} \right) = 100\left( g \right)\)
Đáp án đúng: A
Câu 93:
 Xem đáp án
Xem đáp án
Lời giải
Để tấm ván bị rung lên mạnh nhất thì số bước chân của người trên 1s bằng số dao động của tấm ván trên 1s (cộng hưởng cơ)
Ta có, tần số dao động của tấm ván chính là số dao động của tấm ván trên 1s là 0,5 Hz
=> Số bước chân của người trên 1s là 0,5 bước
=> Trong 12 s người đi qua tấm ván với 12.0,5 = 6 bước thì tấm ván rung lên mạnh nhất
Đáp án đúng: B
Câu 94:
 Xem đáp án
Xem đáp án
Lời giải
Tần số dao động càng lớn thì tần số góc càng lớn, suy ra cơ năng càng lớn nên dao động tắt dần càng chậm do lâu mất hết cơ năng.
Đáp án đúng: ACâu 95:
 Xem đáp án
Xem đáp án
Lời giải
Hình chiếu của AB, BC, CA trên phương của đường sức:
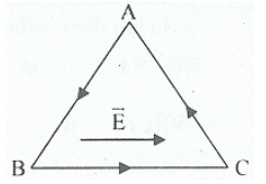
\(\left\{ \begin{array}{l}{d_{AB}} = AB.\cos {120^0} = - 5\left( {cm} \right)\\{d_{BC}} = BC.\cos {0^0} = 10\left( {cm} \right)\\{d_{CA}} = CA.\cos {120^0} = - 5\left( {cm} \right)\end{array} \right.\)
Công của điện tích khi di chuyển từ A đến B:
\({A_{AB}} = qE{d_{AB}} = {10^{ - 8}}.3000.\left( { - 0,05} \right) = - {1,5.10^{ - 6}}\left( J \right)\)
Công của điện tích khi di chuyển từ B đến C:
\({A_{BC}} = qE{d_{BC}} = {10^{ - 8}}.3000.\left( {0,1} \right) = {3.10^{ - 6}}\left( J \right)\)
Công của điện tích khi di chuyển từ C đến A:
\({A_{CA}} = qE{d_{CA}} = {10^{ - 8}}.3000.\left( { - 0,05} \right) = - {1,5.10^{ - 6}}\left( J \right)\)
Đáp án đúng: C
Câu 96:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: T1 = 0,02 s , T2 = 0,01 s.
=> T1 = 2T2 => Trong cùng một khoảng thời gian số lần đổi chiều của dòng f2 gấp 2 lần dòng f1 (trong một chu kì dòng điện đổi chiều 2 lần).
Đáp án đúng: C
Câu 97:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
+ Vận tốc đổi chiều khi qua vị trí biên.
+ Gia tốc đổi chiều khi vị trí cân bằng.
Vậy phát biểu sai là: Khi chất điểm đi qua vị trí cân bằng, gia tốc và vận tốc đổi chiều.
Đáp án đúng: C
Câu 98:
 Xem đáp án
Xem đáp án
Lời giải
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow \left| v \right| = \omega \sqrt {{A^2} - {x^2}} \)
⇒ A sai
Đáp án đúng: A
Câu 99:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: P = UIcosφ = UIcos(π/2) = 0 W
Đáp án đúng: DCâu 100:
 Xem đáp án
Xem đáp án
Lời giải
Do u và i cùng pha nên mạch có R: \(R = \frac{{{U_0}}}{{{I_0}}} = \frac{{220\sqrt 2 }}{{2\sqrt 2 }} = 110\Omega \)
Đáp án đúng: B
Câu 101:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\omega = \frac{1}{{\sqrt {LC} }} = {5.10^5}\left( {rad/s} \right)\)
Phương trình cường độ dòng điện: \(i = {I_0}\cos \left( {\omega t + \varphi } \right)\)
Chọn \(t = 0\) khi \(i = {I_0}\)
\( \Rightarrow i = {I_0}\cos \varphi = {I_0} \Rightarrow \cos \varphi = 1 \Rightarrow \varphi = 0\)
Vậy \(i = 6\cos \left( {{{5.10}^5}t} \right)\left( {mA} \right)\)
Đáp án đúng: D
Câu 102:
 Xem đáp án
Xem đáp án
Lời giải
Ta có U = 100\(\sqrt 2 \) V => I = U/R = 5\(\sqrt 2 \) A
Vì mạch chỉ có R nên công suất của mạch là P = UI = 1000 W
Đáp án đúng: A
Câu 103:
 Xem đáp án
Xem đáp án
Lời giải
\(I = \frac{U}{R} = \frac{{220}}{{100}} = 2,2\left( A \right)\)
Nhiệt lượng: \(Q = {I^2}Rt = {2,2^2}.100.3600 = 1742400\left( J \right)\)
Đáp án đúng: C
Câu 104:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\omega = \frac{{2\pi }}{T} = \pi \left( {{\rm{rad/s}}} \right);A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 4\left( {cm} \right)\)
Sau \[\frac{1}{2}\] chu kì vật có li độ là \({x_1} = - {x_0} = 2\left( {cm} \right)\)\( \Rightarrow {a_1} = - {\omega ^2}{x_1} = - 20\left( {{\rm{cm/}}{{\rm{s}}^2}} \right)\)
Đáp án đúng: A
Câu 105:
 Xem đáp án
Xem đáp án
Lời giải
Bước sóng của một ánh sáng đơn sắc trong nước: \({\lambda _n} = \frac{{600}}{{\frac{4}{3}}} = 450\left( {mm} \right)\)
Đáp án đúng: D
Câu 106:
 Xem đáp án
Xem đáp án
Lời giải
Gọi t0 là thời điểm nhiệt độ lon nước là 800F: \(T\left( {{t_0}} \right) = 32 + 48.{\left( {0,9} \right)^{{t_0}}} = 80 \Rightarrow {t_0} = 0\)
Gọi t1 là thời điểm nhiệt độ lon nước là 500F: \(T\left( {{t_1}} \right) = 32 + 48.{\left( {0,9} \right)^{{t_1}}} = 50 \Rightarrow {t_1} = 9,3\)
Đáp án đúng: B
Câu 107:
 Xem đáp án
Xem đáp án
Lời giải
Nếu mắc 3 pin nối tiếp thì E = 3.3 = 9 V
Nếu mắc 3 pin song song thì E’ = 3V
Nếu mắc 2 pin song song rồi nối tiếp với 1 pin thì được E = 3 + 3 = 6V
Vậy với 3 pin thì không thể mắc được bộ nguồn có suất điện động 5V
Đáp án đúng: B
Câu 108:
 Xem đáp án
Xem đáp án
Lời giải
ZL = ωL = 100Ω , Zc = 1/ ωC = 50Ω
\(\left| \varphi \right| = \frac{\pi }{4} \Rightarrow \left| {\tan \varphi } \right| = \frac{{\left| {{Z_L} - {Z_C}} \right|}}{R} = 1 \Rightarrow \left| {{Z_L} - {Z_C}} \right| = R = 50\Omega \)
Đáp án đúng: C
Câu 109:
 Xem đáp án
Xem đáp án
Lời giải
Zʟ = 10 Ω, r = 10 Ω
\(I = \frac{U}{Z} = \frac{U}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
=> Imax <=> Zc = Zʟ = 10 Ω => C = 10-3/π (F)
=> Imax = U/(R + r) = 1
=> R = 40 Ω
Đáp án đúng: CCâu 110:
 Xem đáp án
Xem đáp án
Lời giải
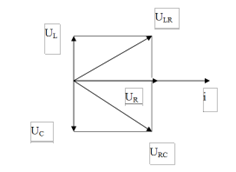
Dựa vào giản đồ vecto ta sẽ thấy đoạn mạch chứa R và C luôn có điện áp trễ pha so với cường độ dòng điện.
Câu 111:
 Xem đáp án
Xem đáp án
Lời giải
\({Z_L} = \omega L = 25\Omega \Rightarrow Z = \sqrt {{{\left( {R + r} \right)}^2} + Z_L^2} = 25\sqrt 2 \Rightarrow {I_0} = \frac{{{U_0}}}{Z} = 4\left( A \right)\)
\[\tan \varphi = \frac{{{Z_L}}}{{R + r}} = \frac{{25}}{{10 + 15}} = 1 \Rightarrow \varphi = \frac{\pi }{4}\] ⇒ i trễ pha hơn u góc \(\frac{\pi }{4}\).
Đáp án đúng: C
Câu 112:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(R = 30\Omega ;{Z_L} = 60\Omega ;{Z_C} = 100\Omega \)
\( \Rightarrow Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = 50\Omega \)
Đáp án đúng: ACâu 113:
 Xem đáp án
Xem đáp án
Lời giải
\(\Delta \ell = \frac{{{T^2}}}{{4{\pi ^2}}}.g = 4\left( {cm} \right)\)
\({t_{dan}} = 2{t_{nen}} \Rightarrow \frac{T}{2} + 2\Delta t = 2\left( {\frac{T}{2} - 2\Delta t} \right) \Rightarrow \Delta t = \frac{T}{{12}}\)
Vậy thời gian đi từ vị trí cân bằng đến hết ∆l mất:
\(\Delta t = \frac{T}{{12}} \Rightarrow \frac{A}{2} = 4 \Rightarrow A = 8\left( {cm} \right) \Rightarrow 2A = L = 16\left( {cm} \right)\)
Đáp án đúng: B
Câu 114:
 Xem đáp án
Xem đáp án
Lời giải
\({Z_L} = L\omega = 25\,\Omega \Rightarrow Z = 25\sqrt 2 \,\Omega \)
\(I = \frac{U}{{\sqrt {{{\left( {R + r} \right)}^2} + Z_L^2} }} = \frac{{100}}{{25\sqrt 2 }} = 2\sqrt 2 \left( A \right)\)
Đáp án đúng: D
Câu 115:
 Xem đáp án
Xem đáp án
Lời giải
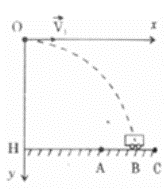
Chọn gốc tọa độ O là điểm cắt bom, t = 0 là lúc cắt bom
Phương trình chuyển động là: \(\left\{ \begin{array}{l}x = {V_1}t\left( 1 \right)\\y = \frac{1}{2}g{t^2}\left( 2 \right)\end{array} \right.\)
Phương trình quỹ đạo: \(y = \frac{1}{2}\frac{g}{{v_0^2}}{x^2}\)
Bom sẽ rơi nhanh theo nhánh Parabol và gặp mặt đường tại B. Bom sẽ trúng xe khi bom và xe cùng lúc đến B.
\( \Rightarrow t = \sqrt {\frac{{2h}}{g}} \)
Lúc t = 0, xe tăng ở A: \(AB = {V_2}t = {V_2}\sqrt {\frac{{2h}}{g}} \)
Khoảng cách khi cắt bom là: \(HA = HB - AB = \left( {{V_1} - {V_2}} \right)\sqrt {\frac{{2h}}{g}} \)
Câu 116:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\left\{ \begin{array}{l}{N_1} = 2{N_2}\\\frac{{{N_1}}}{{{N_2}}} = \frac{{{U_1}}}{{{U_2}}} = \frac{{{I_2}}}{{{I_1}}}\end{array} \right.\)\( \Leftrightarrow \frac{{2{N_2}}}{{{N_2}}} = \frac{{220}}{{{U_2}}} = \frac{{{I_2}}}{1} \Rightarrow \left\{ \begin{array}{l}{U_2} = 110\left( V \right)\\{I_2} = 2\left( A \right)\end{array} \right.\)
Đáp án đúng: D
Câu 117:
 Xem đáp án
Xem đáp án
Lời giải
Công suất điện hao phí trên đường dây tải điện là hiệu số chỉ của các công tơ điện ở trạm phát và ở nơi thu
\( \Rightarrow \Delta P = \frac{A}{t} = \frac{{480}}{{24}} = 20\left( {kWh} \right)\)
Đáp án đúng: A
Câu 118:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({Z_L} = 60\Omega ;{Z_C} = 100\Omega ;U = 80\left( V \right)\)
Công suất tỏa nhiệt trên điện trở: \(P = \frac{{{{\rm{U}}^2}{\rm{R}}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = 80 \Rightarrow R = 40\Omega \)
Đáp án đúng: DCâu 119:
 Xem đáp án
Xem đáp án
Lời giải
Biểu thức định luật Ôm đối với toàn mạch: \(I = \frac{E}{{R + r}}\) hay \(E = {\rm{IR}} + I.r = U + I.r\)
\( \Rightarrow U = E - I.r\)
⇒ I tăng thì U giảm
Đáp án đúng: CCâu 120:
 Xem đáp án
Xem đáp án
Lời giải
\({Z_L} = 70\Omega ;{Z_C} = 50\Omega \Rightarrow Z = 20\sqrt 2 \Omega \)\( \Rightarrow {U_0} = Z{I_0} = 20\sqrt 2 .\sqrt 2 = 40\left( V \right)\)
\(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = 1 \Rightarrow \varphi = \frac{\pi }{4}\)⇒ u sớm pha hơn i góc \(\frac{\pi }{4}\)
Đáp án đúng: B
Câu 121:
 Xem đáp án
Xem đáp án
Lời giải
\(\Delta \varphi = \frac{{2\pi x}}{\lambda } = \frac{{2\pi }}{3}\)
Giải hệ phương trình: \(\left\{ \begin{array}{l}{u_M} = A\cos \alpha = 3\\{u_N} = A\cos \left( {\alpha - \frac{{2\pi }}{3}} \right) = 4\end{array} \right. \Rightarrow A = 7\left( {cm} \right)\)
Đáp án đúng: C
Câu 122:
 Xem đáp án
Xem đáp án
Lời giải
Vì dòng xoay chiều biến thiên điều hòa theo thời gian nên giá trị trung bình của nó trong một chu kỳ luôn bằng không. Do T rất nhỏ so với thời gian dài t nên coi t ≈ nT => giá trị trung bình của dòng điện xoay chiều trong thời gian t xấp xỉ bằng 0.
Đáp án đúng: DCâu 123:
 Xem đáp án
Xem đáp án
Lời giải
Khi nguồn âm tại O: A và C có cùng mức cường độ âm suy ra: OA = OC
Ta có: \({I_C} = \frac{P}{{4\pi O{C^2}}} \Rightarrow {L_C} = \log \left( {\frac{P}{{4\pi O{C^2}.{I_0}}}} \right) = 3\left( B \right)\)
Lúc sau, nguồn âm tại B thì mức cường độ âm tại O và C bằng nhau nên BO = BC
\({I'_C} = \frac{{10P/3}}{{4\pi B{C^2}}} \Rightarrow {L'_C} = \log \left( {\frac{{10P/3}}{{4\pi B{C^2}.{I_0}}}} \right) = 4\left( B \right)\)
Suy ra: \({L'_C} - {L_C} = \log \left( {\frac{{10}}{3}.\frac{{O{C^2}}}{{B{C^2}}}} \right) = 1 \Rightarrow OC = BC\sqrt 3 \)
Áp dụng định lý cosin trong tam giác OBC \( \Rightarrow \widehat {OBC} = {120^0}\)
\( \Rightarrow \widehat {AOC} = {120^0} \Rightarrow AC = \sqrt 3 OC = 3BC \Rightarrow BA = AC - BC = 2BC\)
\( \Rightarrow \frac{{{I_A}}}{{{I_C}}} = {\left( {\frac{{BC}}{{BA}}} \right)^2} = {10^{{L_A} - 4}} = \frac{1}{4} \Rightarrow {L_A} = 3,4\left( B \right) = 34\left( {dB} \right)\)
Đáp án đúng: ACâu 124:
 Xem đáp án
Xem đáp án
Lời giải
Cường độ dòng điện hiệu dụng là \(\frac{1}{{\sqrt 2 }}\left( A \right)\)
Đáp án đúng: B
Câu 125:
 Xem đáp án
Xem đáp án
Lời giải
Tác dụng chính của biến trở là để tránh hiện tượng đoản mạch.
Đáp án đúng: D
Câu 126:
 Xem đáp án
Xem đáp án
Lời giải
Ampe kế cho biết giá trị hiệu dụng của cường độ dòng điện chạy qua ampe kế.
Đáp án đúng: D
Câu 127:
 Xem đáp án
Xem đáp án
Lời giải
Hiệu điện thế giữa hai đầu mạch ngoài: \(\overrightarrow T + \overrightarrow F + \overrightarrow P = \overrightarrow 0 \Rightarrow \overrightarrow T + \overrightarrow R = \overrightarrow 0 \)
Đáp án đúng: A
Câu 128:
 Xem đáp án
Xem đáp án
Lời giải
Có 2 giá trị của C cho cùng giá trị công suất:
\( \Rightarrow {P_1} = {P_2} \Rightarrow {\left( {{Z_L} - {Z_{C1}}} \right)^2} = {\left( {{Z_L} - {Z_{{C_2}}}} \right)^2} \Rightarrow 2{Z_L} = {Z_{C1}} + {Z_{C2}}\)
\( \Rightarrow {Z_L} = \frac{{400 + 200}}{2} = 300\Omega \Rightarrow L = \frac{3}{\pi }\left( H \right)\)
Đáp án đúng: D
Câu 129:
 Xem đáp án
Xem đáp án
Lời giải
Đèn có: \(R = 12\Omega ;{I_{dm}} = 0,5A\)
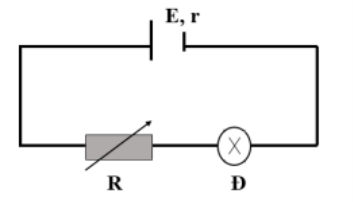
Đèn sáng bình thường nên dòng điện qua đèn là I = 0,5 A
Áp dụng định luật Ôm đối với toàn mạch: \(I = \frac{E}{{r + {R_b} + {R_d}}} = 0,5 \Rightarrow {R_b} = 5\Omega \)
Đáp án đúng: B
Câu 130:
 Xem đáp án
Xem đáp án
Lời giải
Công suất tiêu thụ của hai điện trở như nhau nên ta có:
\(P = I_1^2{R_1} = I_2^2{R_2}\)\( \Rightarrow \frac{{{E^2}}}{{{{\left( {r + {R_1}} \right)}^2}}}{R_1} = \frac{{{E^2}}}{{{{\left( {r + {R_2}} \right)}^2}}}{R_2} \Rightarrow \frac{1}{{{{\left( {r + 1} \right)}^2}}} = \frac{9}{{{{\left( {r + 9} \right)}^2}}} \Rightarrow r = 3\Omega \)
Đáp án đúng: B
Câu 131:
 Xem đáp án
Xem đáp án
Lời giải
Phương pháp: Vận dụng biểu thức tính công suất: \(P = \frac{{{U^2}}}{R}\)
Cách giải:
+ Trong mạch điện 1 chiều, công suất tiêu thụ của mạch: \({P_0} = \frac{{U_0^2}}{R}\)
+ Trong mạch điện xoay chiều, công suất tiêu thụ của mạch: \(P = \frac{{U_{}^2}}{R} = \frac{{U_0^2}}{{2R}} \Rightarrow \frac{{{P_0}}}{P} = 2\)
Đáp án đúng: D
Câu 132:
 Xem đáp án
Xem đáp án
Lời giải
Công của lực điện trường trên đường gấp khúc ABC là
\(\begin{array}{l}{A_{ABC}} = {A_{AB}} + {A_{BC}}\\{A_{AB}} = qE{d_1} = q.E.AB.\cos {30^0} = {6,92.10^{ - 5}}\left( J \right)\\{A_{BC}} = qE{d_2} = q.E.BC.\cos {120^0} = - {8.10^{ - 5}}\left( J \right)\end{array}\)
\( \Rightarrow {A_{ABC}} = - {1,08.10^{ - 5}}\left( J \right)\)
Đáp án đúng: BCâu 133:
 Xem đáp án
Xem đáp án
Lời giải
Phân tích các lực tác dụng vào quả cầu ta có:
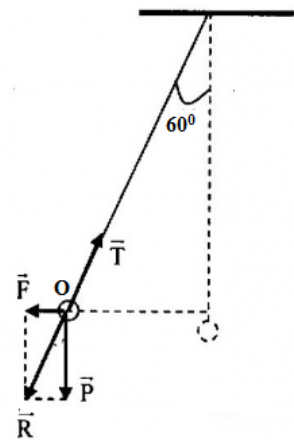
Ta có: \(\overrightarrow T + \overrightarrow F + \overrightarrow P = \overrightarrow 0 \Rightarrow \overrightarrow T + \overrightarrow R = \overrightarrow 0 \)
Từ hình vẽ có: \(\tan {60^0} = \frac{F}{P} = \frac{{\left| q \right|E}}{{m.g}} \Rightarrow E = 1732\left( {V/m} \right)\)
Đáp án đúng: BCâu 134:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(E = \frac{F}{q} = 20000\left( {{\rm{V/m}}} \right)\)
Đáp án đúng: D
Câu 135:
 Xem đáp án
Xem đáp án
Lời giải
Một đèn loại 220 V – 75 W và một đèn loại 220 V – 25 W → Pđm1 = 3.Pđm2
Hai đèn được sử dụng đúng hiệu điện thế định mức → Ptt1 = 3.Ptt2
Ta có: \(A = P.t \Rightarrow \left\{ \begin{array}{l}{A_1} = {P_{tt1}}.t\\{A_2} = {P_{tt2}}.t\end{array} \right. \Rightarrow {A_1} = 3{A_2}\)
Đáp án đúng: B
Câu 136:
 Xem đáp án
Xem đáp án
Lời giải
Khoảng cách giữa hai vân sáng liên tiếp là: \(i = \frac{{\lambda D}}{a} = 0,5\left( {mm} \right)\)
Đáp án đúng: A
Câu 137:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
+ Khi dùng ánh sáng có bước sóng λ1 thì trên MN có 10 vân tối => có 11 vân sáng
=> Đoạn MN = 20mm = 10i => i = 2mm
+ Khi thay λ1 bằng bước sóng λ2 thì có khoảng vân i’
\(\frac{{i'}}{i} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{5}{3} \Rightarrow i' = \frac{5}{3}i = \frac{{10}}{3}\left( {mm} \right)\)
=> số vân sáng trên đoạn MN: \({N_s} = 2\left[ {\frac{L}{{2i'}}} \right] + 1 = 2.3 + 1 = 7\)
Đáp án đúng: ACâu 138:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: q = U.C => q’ = 2U.C = 2q.
Đáp án đúng: C
Câu 139:
 Xem đáp án
Xem đáp án
Lời giải
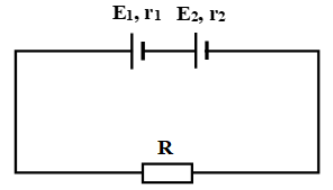
Định luật Ôm cho toàn mạch: \(I = \frac{{{E_1} + {E_2}}}{{R + {r_1} + {r_2}}} \Rightarrow R = \frac{{{E_1} + {E_2}}}{I} - \left( {{r_1} + {r_2}} \right) = 2,5\Omega \)
Đáp án đúng: DCâu 140:
 Xem đáp án
Xem đáp án
Lời giải
Giả sử năng lượng ban đầu của con lắc là \[{{\rm{W}}_1} = \frac{1}{2}kA_1^2\]
Sau một chu kì, năng lượng của con lắc là \[{{\rm{W}}_2} = \frac{1}{2}kA_2^2\]
Mà cứ sau mỗi chu kì, biên độ giảm 3% nên A2 = A1 - 0,03 A1 = 0,97 A1
Vậy phần năng lượng của con lắc bị mất đi trong một dao động toàn phần là
\(\frac{{\Delta {\rm{W}}}}{{\rm{W}}} = \frac{{{{\rm{W}}_1} - {{\rm{W}}_2}}}{{{{\rm{W}}_1}}} = \frac{{\frac{1}{2}kA_1^2 - \frac{1}{2}kA_2^2}}{{\frac{1}{2}kA_1^2}} = \frac{{A_1^2 - {{\left( {0,97A_1^{}} \right)}^2}}}{{A_1^2}} = 0,06\left( { = 6\% } \right)\)
Câu 141:
 Xem đáp án
Xem đáp án
Lời giải
Lực tương tác giữa hai điện tích trong hai trường hợp lần lượt là:
\(\left\{ \begin{array}{l}{F_1} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{r_1^2}} = {1,6.10^{ - 4}}\left( N \right)\\{F_2} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{r_2^2}} = {2,5.10^{ - 4}}\left( N \right)\end{array} \right. \Rightarrow \frac{{{F_1}}}{{{F_2}}} = \frac{{r_2^2}}{{r_1^2}} = 0,64\)
\( \Rightarrow \frac{{{r_2}}}{{{r_1}}} = 0,8 \Rightarrow {r_2} = 0,8{r_1} = 0,8.2 = 1,6\left( {cm} \right)\)
Đáp án đúng: CCâu 142:
 Xem đáp án
Xem đáp án
Lời giải
Do dây có 1 đầu cố định 1 đầu tự do và có 9 bụng sóng, suy ra k = 8
\( \Rightarrow \ell = \left( {2.8 + 1} \right)\frac{\lambda }{4} = \frac{{17}}{4}\lambda \Rightarrow \lambda = \frac{{24}}{{85}}\left( m \right)\)
Lại có: \(v = \lambda .f = 24\left( {m/s} \right)\)
Đáp án đúng: B
Câu 143:
 Xem đáp án
Xem đáp án
Lời giải
Giá trị của R để công suất tiêu thụ trên biến trở là cực đại: \(R = {Z_d} = \sqrt {{r^2} + Z_L^2} \)
→ Từ giản đồ vecto ta có: r = 10 Ω và \({Z_L} = 10\sqrt 3 \Omega \)
→ Giá trị của biến trở để công suất tiêu thụ trên toàn mạch là cực đại
\(R = {Z_L} - r = 10\sqrt 3 - 10 = 7,3\Omega \)
Đáp án đúng: D
Câu 144:
 Xem đáp án
Xem đáp án
Lời giải
Dựa vào đồ thị ta thấy tại một thời điểm bất kì u luôn nhanh pha hơn i một góc π/2 nên chứng tỏ đoạn mạch chỉ chứa cuộn dây thuần cảm.
Đáp án đúng: CCâu 145:
 Xem đáp án
Xem đáp án
Lời giải
Quãng đường âm truyền đi rồi phản xạ trở lại là: s = 2L
Thời gian âm truyền đi rồi phản xạ trở lại là: \(t = \frac{s}{v} = \frac{{2L}}{v}\)
Để không nghe được tiếng nổ, ta có: \(t \le 0,1 \Rightarrow \frac{{2L}}{v} \le 0,1 \Rightarrow L \le \frac{{0,1v}}{2} = \frac{{0,1.340}}{2} = 17\left( m \right)\)
Đáp án đúng: BCâu 146:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(v = \lambda .f \Rightarrow \lambda = \frac{v}{f} = 2\left( m \right)\)
Lại có khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \[\frac{1}{2}\] bước sóng => d = 1 m.
Đáp án đúng: B
Câu 147:
 Xem đáp án
Xem đáp án
Lời giải
Nhận định "Từ trường của ống dây là từ trường vĩnh cửu" là không đúng khi nói về ống dây có dòng điện chạy qua.
Đáp án đúng: D
Câu 148:
 Xem đáp án
Xem đáp án
Lời giải
Quá trình truyền sóng không phải là quá trình truyền vật chất.
Đáp án đúng: A
Câu 149:
 Xem đáp án
Xem đáp án
Lời giải
Ta có hệ số công suất của đoạn mạch được xác định bởi công thức:
\(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{C\omega }}} \right)}^2}} }} \Rightarrow \left\{ \begin{array}{l}\cos \varphi \notin U\\\cos \varphi \in R,L,C,f\end{array} \right.\)
Đáp án đúng: A
Câu 150:
 Xem đáp án
Xem đáp án
Lời giải
Tại M có 4 vân trùng: \({k_1}.735 = {k_2}.490 = {k_3}{\lambda _3} = {k_4}{\lambda _4}\left( 1 \right)\)
\(\frac{{{k_1}}}{{{k_2}}} = \frac{{490}}{{735}} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}{k_1} = 2n\\{k_2} = 3n\end{array} \right. \Rightarrow {x_M} = \frac{{2n.735.D}}{a} = \frac{{1470nD}}{a}\)
Tại M ngoài hai bức xạ 735 nm và 490 nm cho vân sáng thì còn có hai bức xạ khác cũng cho vân sáng.
\(\begin{array}{l} \Rightarrow {x_M} = \frac{{1470nD}}{a} = \frac{{k\lambda D}}{a} \Rightarrow \lambda = \frac{{1470n}}{k}\\ \Rightarrow 380 \le \frac{{1470nD}}{a} \le 760 \Rightarrow 1,93n \le k \le 3,87n\end{array}\)
Với \(n = 1 \Rightarrow 1,93 \le k \le 3,87 \Rightarrow k = 2;3\)
⇒ Tại M có hai bức xạ cho vân sáng (Loại)
Với \(n = 2 \Rightarrow 3,86 \le k \le 7,74 \Rightarrow k = 4;5;6;7\)
⇒ Tại M có 4 bức xạ cho vân sáng ứng với:
\({\lambda _1} = \frac{{1470.2}}{4} = 735\left( {nm} \right);{\lambda _2} = \frac{{1470.2}}{6} = 490\left( {nm} \right);\)
\({\lambda _3} = \frac{{1470.2}}{5} = 588\left( {nm} \right);\,{\lambda _4} = \frac{{1470.2}}{7} = 420\left( {nm} \right)\)
\( \Rightarrow {\lambda _3} + {\lambda _4} = 588 + 420 = 1008\left( {nm} \right)\)
Đáp án đúng: C
Câu 151:
 Xem đáp án
Xem đáp án
Lời giải
Sóng vô tuyến truyền được qua tầng điện li ra ngoài không gian là sóng cực ngắn
Đáp án đúng: C
Câu 152:
 Xem đáp án
Xem đáp án
Lời giải
Vì Uᴀɴ vuông pha với Uᴍʙ
=> tan φᴀɴ. tan φᴍʙ= -1 => \(\frac{{{Z_L}}}{R}.\frac{{{Z_C}}}{R} = 1 \Rightarrow R = \sqrt {{Z_L}.{Z_C}} = 50\Omega \)
Đáp án đúng: C
Câu 153:
 Xem đáp án
Xem đáp án
Lời giải
Do chiết suất của nước đối với các tia tăng theo thứ tự:
\({n_{cham}} < {n_{luc}} < {n_{cam}} \Rightarrow {r_{cam}} > {r_{luc}} > {r_{cham}}\)
→ Đi từ mặt nước lên ta lần lượt gặp các tia chàm, lục, da cam.
Câu 154:
 Xem đáp án
Xem đáp án
Lời giải
+ Biên độ dao động khi có sự cộng hưởng cơ phụ thuộc vào lực cản của môi trường.
Đáp án đúng: D
Câu 155:
 Xem đáp án
Xem đáp án
Lời giải
Khi đưa một đầu của thanh nam châm thẳng lại gần một đầu của ống dây có dòng điện thì chúng hút hoặc đẩy nhau.
Đáp án đúng: B
Câu 156:
 Xem đáp án
Xem đáp án
Lời giải
Quỹ đạo chuyển động 14 cm => Biên độ dao động A = 7 cm
Chu kỳ T = 1 s
Từ đường tròn lượng giác ta thấy:
Gia tốc của chất điểm có độ lớn cực đại khi chất điểm ở vị trí biên. Trong một chu kì chất điểm đi qua vị trí biên 2 lần, do vậy thời gian để chất điểm đi từ vị trí ban đầu đến khi gia tốc có độ lớn cực tiểu lần thứ 3 sẽ là: \(t = T + \frac{T}{6}\)
Vậy vận tốc trung bình của vật là: \({v_{tb}} = \frac{s}{t} = \frac{{4.7 + \frac{7}{2}}}{{1 + \frac{1}{6}}} = 27\left( {{\rm{cm/s}}} \right)\)
Đáp án đúng: CCâu 157:
 Xem đáp án
Xem đáp án
Lời giải
Công suất toàn mạch cực đại khi và chỉ khi: \(R + r = \left| {{Z_L} - {Z_C}} \right| = 15\Omega \Rightarrow R = 5\Omega \)
Công suất toàn mạch: \(P = \frac{{{U^2}}}{{2\left( {R + r} \right)}} = \frac{{{{60}^2}}}{{2.\left( {5 + 10} \right)}} = 120\left( {\rm{W}} \right)\)
Đáp án đúng: ACâu 158:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\left\{ \begin{array}{l}{T_1} = 2\pi \sqrt {\frac{{{\ell _1}}}{g}} = 10\left( s \right)\\{T_2} = 2\pi \sqrt {\frac{{{\ell _2}}}{g}} = 8\left( s \right)\\T = 2\pi \sqrt {\frac{{{\ell _1} - {\ell _2}}}{g}} \Rightarrow {T^2} = 4{\pi ^2}\frac{{{\ell _1}}}{g} - 4{\pi ^2}\frac{{{\ell _2}}}{g} = T_1^2 - T_2^2\end{array} \right.\)\( \Rightarrow T = \sqrt {T_1^2 - T_2^2} = 6\left( s \right)\)
Đáp án đúng: DCâu 159:
 Xem đáp án
Xem đáp án
Lời giải
Tần số góc: \(\omega = \sqrt {\frac{g}{\ell }} = \pi \left( {rad/s} \right)\)
Phương trình của dao động điều hòa: \(s = {S_0}\cos \left( {\omega t + \varphi } \right)\)
Vận tốc: \(v = s' = \omega {S_0}\cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\left( {cm/s} \right)\)
Áp dụng phương trình độc lập với thời gian:
\({\left( {\frac{s}{{{S_0}}}} \right)^2} + {\left( {\frac{v}{{{v_0}}}} \right)^2} = 1 \Leftrightarrow \frac{{{5^2}}}{{{{10}^2}}} + \frac{{{v^2}}}{{{\pi ^2}{{.10}^2}}} = 1 \Rightarrow v = 27\left( {cm/s} \right)\)
Đáp án đúng: CCâu 160:
 Xem đáp án
Xem đáp án
Lời giải
Phương trình dao động của con lắc đơn dao động điều hoà: s = Socos(ωt + φ)
\(g = {\pi ^2};\ell = 1\left( m \right) \Rightarrow \omega = \sqrt {\frac{g}{\ell }} = \pi \left( {rad/s} \right)\)
Ban đầu giữ vật nhỏ của con lắc ở vị trí có li độ góc là -90 rồi thả nhẹ nên biên độ góc là: \({\alpha _0} = {9^0} = \frac{\pi }{{20}}\left( {rad} \right) \Rightarrow {S_0} = {\alpha _0}\ell = \frac{\pi }{{20}}\left( m \right) = 5\pi \left( {cm} \right)\)
Tại t = 0, vật ở biên âm nên pha ban đầu: \(\varphi = \pi \left( {rad} \right)\)
Phương trình của li độ: s = 5πcos(πt + π) (cm).
Đáp án đúng: CCâu 161:
 Xem đáp án
Xem đáp án
Lời giải
Khi xảy ra cộng hưởng, chu kì dao động của lực cưỡng bức bằng chu kì dao động riêng của hệ
Ta có: \(T = 2\pi \sqrt {\frac{\ell }{g}} = 2\pi \sqrt {\frac{{0,7}}{{10}}} = 1,66\left( s \right)\)
Đáp án đúng: A
Câu 162:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(AB = 100\left( {cm} \right);BC = 150\left( {cm} \right) \Rightarrow BC = 1,5AB\)
Lúc đầu: \(100 = 10\log \left( {\frac{{{I_B}}}{{{I_0}}}} \right) = 10\log \left( {\frac{P}{{{I_0}.4\pi A{B^2}}}} \right) \Rightarrow \frac{P}{{{I_0}.4\pi A{B^2}}} = {10^{10}}\)
Khi đặt nguồn âm 2P tại B:
\({L_A} = 10\log \left( {\frac{{2P}}{{{I_0}4\pi B{A^2}}}} \right) = 10\log \left( {{{2.10}^{10}}} \right) = 103\left( {dB} \right)\)
\({L_B} = 10\log \left( {\frac{{2P}}{{{I_0}.4\pi B{C^2}}}} \right) = 10\log \left( {\frac{{2P}}{{{I_0}.4\pi {{.1,5}^2}A{B^2}}}} \right) = 99,5\left( {dB} \right)\)
Đáp án đúng: ACâu 163:
Chọn câu sai trong các câu sau: Mạch điện xoay chiều RLC nối tiếp đang xảy ra cộng hưởng. Nếu thay đổi tần số của điện áp đặt vào hai đầu mạch thì:
 Xem đáp án
Xem đáp án
Lời giải
Nếu thay đổi tần số của điện áp đặt vào hai đầu mạch thì điện áp hiệu dụng trên L giảm là sai.
Đáp án đúng: A
Câu 164:
 Xem đáp án
Xem đáp án
Lời giải
Biểu thức của suất điện động tự cảm 2 đầu cuộn cảm là:
\(e = - Li' = L\omega {I_0}\sin \left( {100\pi t + \frac{\pi }{3}} \right) = 200\sin \left( {100\pi t + \frac{\pi }{3}} \right)\)
⇒ Suất điện động tự cảm tại thời điểm 0,5112 s là: -197,85 V
Đáp án đúng: D
Câu 165:
 Xem đáp án
Xem đáp án
Lời giải
Thời điểm ban đầu t = 0 và thời điểm t vật qua vị trí cân bằng lần đầu tiên được biểu diễn trên đường tròn lượng giác:
Góc quét: α = π/6 + π/2 = 2π/3 (rad) \( \Rightarrow t = \frac{\alpha }{\omega } = \frac{1}{3}\left( s \right)\)
Đáp án đúng: A
Câu 166:
 Xem đáp án
Xem đáp án
Lời giải
Đặt biên độ góc của dao động thành phần thứ nhất là: a
Biên độ góc của dao động thành phần thứ hai là: b
Nên biên độ góc của dao động tổng hợp là (a + b)/2
Góc lệch pha so với dao động thành phần thứ nhất là 900 nên biên độ dao động tổng hợp là: \(\sqrt {{b^2} - {a^2}} \)
Ta được: \(\frac{{a + b}}{2} = \sqrt {{b^2} - {a^2}} \Rightarrow \frac{a}{b} = \frac{3}{5}\)
Góc lệch của hai dao động thành phần là: \(\Delta \varphi = 180 - \arccos \frac{a}{b} = {126,9^0}\)
Đáp án đúng: BCâu 167:
 Xem đáp án
Xem đáp án
Lời giải
Khi gia tốc của vật có độ lớn là 100 cm/s2 thì li độ của vật có độ lớn là x0.
Ta có hình vẽ
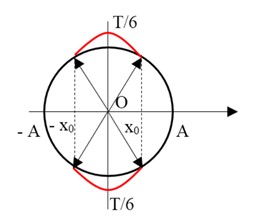
Từ hình vẽ suy ra: \[{x_0} = \frac{A}{2} = 2,5\,cm\]
Thay vào công thức:
\[a = {\omega ^2}\left| x \right| \Rightarrow \omega = \sqrt {\frac{a}{{\left| x \right|}}} = \sqrt {\frac{{100}}{{2,5}}} = 2\sqrt {10} = 2\pi \,\left( {rad/s} \right) \Rightarrow f = 1\,Hz\]
Đáp án đúng: D
Câu 168:
 Xem đáp án
Xem đáp án
Lời giải
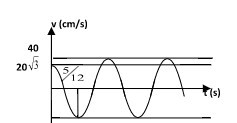
Lúc t = 0: \(v = 20\sqrt 3 \Rightarrow \sin \varphi = - \frac{{\sqrt 3 }}{2}\)và do vận tốc đang giảm nên vật ở li độ dương và đang đi về biên dương.
\( \Rightarrow \varphi = - \frac{\pi }{3} \Rightarrow x = A\cos \left( { - \frac{\pi }{3}} \right) = \frac{A}{2}\)
Thời gian tương ứng từ x = A/2 đến vị trí cân bằng theo chiều âm lần thứ nhất:
\(t = \frac{T}{6} + \frac{T}{4} = \frac{5}{{12}}T = \frac{5}{{12}}(s) \Rightarrow T = 1 \Rightarrow \omega = 2\pi \left( {rad/s} \right) \Rightarrow A = \frac{{{v_{\max }}}}{\omega } = \frac{{40}}{{2\pi }} = 2\sqrt {10} \left( {cm} \right)\)
Vậy \(x = 2\sqrt {10} \cos \left( {2\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
Đáp án đúng: CCâu 169:
 Xem đáp án
Xem đáp án
Lời giải
Ta có, điện năng tiêu thụ của mạch: A = UIt = \(\frac{{{U^2}}}{R}t\)
Khi điện trở trong mạch được điều chỉnh tăng 2 lần thì cùng khoảng thời gian điện năng tiêu thụ sẽ giảm 2 lần.
Đáp án đúng: A
Câu 170:
 Xem đáp án
Xem đáp án
Lời giải
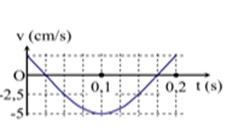
Từ đồ thị ta có độ chia nhỏ nhất của mỗi ô là: 0,025 s
Mặt khác: \[\frac{1}{2}\] chu kì ứng với 6 ô \( \Rightarrow \frac{T}{2} = 0,15\left( s \right) \Rightarrow T = 0,3\left( s \right) \Rightarrow \omega = \frac{{20\pi }}{3}\left( {rad/s} \right)\)
Khi t = 0 thì \(v = \frac{{{v_{max}}}}{2}\) và đang giảm \( \Rightarrow \varphi = - \frac{\pi }{6}\)
\(A = \frac{{{v_{max}}}}{\omega } = \frac{3}{{4\pi }}\left( {cm} \right)\)⇒ \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)\left( {cm} \right)\)
Đáp án đúng: DCâu 171:
 Xem đáp án
Xem đáp án
Lời giải
\(\omega = \sqrt {\frac{g}{{\Delta \ell }}} \Rightarrow \Delta \ell = 0,1\left( m \right) = 10\left( {cm} \right)\)
Đáp án đúng: BCâu 172:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
+ lực căng dây cực đại tại vị trí α = 0: \({T_{max}} = mg\left( {3 - 2\cos {\alpha _0}} \right)\)
+ lực căng dây cực tiểu tại vị trí α = α0: \({T_{\min }} = mg\cos {\alpha _0}\)
\( \Rightarrow \frac{{{T_{max}}}}{{{T_{\min }}}} = \frac{{3 - 2\cos {\alpha _0}}}{{\cos {\alpha _0}}} = 1,02 \Rightarrow {\alpha _0} = {6,6^0}\)
Đáp án đúng: BCâu 173:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(T \sim \sqrt \ell \Rightarrow \frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{{{\ell _2}}}{{{\ell _1}}}} = 0,9 \Rightarrow {\ell _2} = {0,9^2}.{\ell _1} = 97,2\,cm \Rightarrow \Delta \ell = {\ell _1} - {\ell _2} = 22,8\left( {cm} \right)\)
Vậy phải giảm chiều dài của con lắc đi 22,8 cm.
Đáp án đúng: C
Câu 174:
 Xem đáp án
Xem đáp án
Lời giải
Do q1 và q2 cùng dấu nên để lực tổng hợp tác dụng lên điện tích q0 bằng 0, điểm M phải nằm trên đường nối hai điện tích, và nằm trong khoảng giữa hai điện tích.
Lực do hai điện tích tác dụng lên điện tích q0 là: \(\left\{ \begin{array}{l}{F_1} = k\frac{{{q_1}{q_0}}}{{r_1^2}}\\{F_2} = k\frac{{{q_2}{q_0}}}{{r_2^2}}\end{array} \right.\)
Lực tổng hợp tác dụng lên điện tích q0 bằng 0, ta có:
\({\vec F_1} + {\vec F_2} = 0 \Rightarrow {F_1} = {F_2} \Rightarrow {r_1} = {r_2}\)
Do M nằm giữa hai điện tích nên \({r_1} + {r_2} = d \Rightarrow {r_1} = {r_2} = \frac{d}{2}\)
Đáp án đúng: D
Câu 175:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({v_{max}} = \sqrt {2g\ell \left( {1 - \cos {5^0}} \right)} \)
\(s_0^2 = \frac{{v_{max}^2}}{{{\omega ^2}}} = \frac{{2g\ell \left( {1 - \cos {5^0}} \right)}}{{\frac{g}{{\frac{\ell }{2}}}}} \Rightarrow {\alpha _0} = 0,123\left( {rad} \right) = {7,1^0}\)
Đáp án đúng: ACâu 176:
 Xem đáp án
Xem đáp án
Lời giải
Biên độ dao động: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } = 5\sqrt 3 \left( {cm} \right)\)
\({\left| {{F_{kv}}} \right|_{max}} = m{\omega ^2}A = 0,5\sqrt 3 \left( N \right)\)
Đáp án đúng: DCâu 177:
 Xem đáp án
Xem đáp án
Lời giải
Ta có hình vẽ biểu diễn các lực tác dụng vào quả cầu:
Trọng lực của quả cầu: P = m.g = 0,25.10−3.10 = 2,5.10−3N
Lực điện tác dụng lên quả cầu mang điện: Fd = qE = 2,5.10−9.106 = 2,5.10−3 N
Từ hình vẽ ta có: \(\tan \alpha = \frac{{{F_d}}}{P} = 1 \Rightarrow \alpha = {45^0}\)
Đáp án đúng: B
Câu 178:
 Xem đáp án
Xem đáp án
Lời giải
Trong giao thoa của hai sóng trên mặt nước từ hai nguồn kết hợp, ngược pha nhau, những điểm dao động với biên độ cực tiểu có hiệu khoảng cách tới hai nguồn (k ∈ Z) là: d2 – d1 = kλ
Đáp án đúng: A
Câu 179:
 Xem đáp án
Xem đáp án
Lời giải
Các tính chất điện của bán dẫn
- Điện trở suất của bán dẫn có giá trị trung gian giữa kim loại và điện môi.
- Điện trở suất của bán dẫn giảm mạnh khi nhiệt độ tăng.
- Điện trở suất của bán dẫn phụ thuộc vào các tạp chất có trong tinh thể.
Đáp án đúng: C
Câu 180:
 Xem đáp án
Xem đáp án
Lời giải
Hệ số công suất của đoạn mạch: \(\cos \varphi = \frac{R}{Z} = \frac{{{U_R}}}{U} = \frac{{100}}{{200}} = 0,5\)
Đáp án đúng: DCâu 181:
 Xem đáp án
Xem đáp án
Những đặc điểm của lực đàn hồi lò xo:
- Điểm đặt: Đặt lên vật tiếp xúc với lò xo làm lo xo biến dạng.
- Phương: Trùng với trục lò xo.
- Chiều: Khi bị dãn, lực đàn hồi của lò xo hướng vào trong; Khi nị nén, lực đàn hồi lướng ra ngoài (ngược chiều biến dạng).
Độ lớn: Fđh = k.| ∆l|
Câu 182:
 Xem đáp án
Xem đáp án
Lời giải
Tại điểm M: \(\frac{{{d_2} - {d_1}}}{\lambda } = 3\) nên M là điểm thuộc vân giao thoa cực đại thứ 3.
Vì vậy, giữa M và đường trung trực của đoạn thẳng S1S2 có 3 vân giao thoa cực tiểu là các cực tiểu thứ 1, 2, 3.
Đáp án đúng: D
