Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1) Chứng minh: SD là tiếp tuyến của đường tròn (O).
2) Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3) Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH\,.\,KD\).
 Giải bởi Vietjack
Giải bởi Vietjack
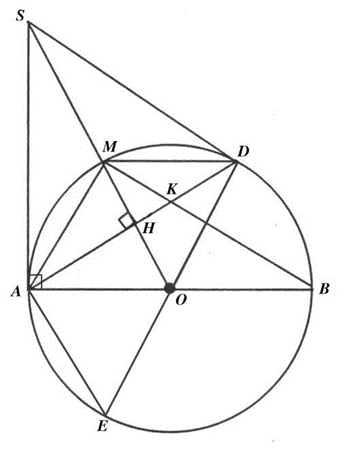
1) Xét ∆OAB có \(\left\{ \begin{array}{l}OA = OD = R\\OH \bot AD\end{array} \right.\)
Þ ∆OAD cân tại O có OH là đường cao
Þ OH là đường phân giác của \(\widehat {AOD}\)
\[ \Rightarrow \widehat {AOH} = \widehat {DOH}\]hay\[\widehat {AOS} = \widehat {DOS}\]
Xét ∆SAO và ∆SDO có:
KO chung
\[\widehat {AOS} = \widehat {DOS}\]
OA = OD = R
Do đó ∆SAO = ∆SDO (c.g.c)
Mà \(\widehat {SAO} = 90^\circ \) (SA ^ OA do SA là tiếp tuyến của (O) tại A)
\( \Rightarrow \widehat {SDO} = 90^\circ \)hay SD ^ OD
Suy ra SD là tiếp tuyến của (O) tại D.
2) ∆OAM có OA = OM = R
Þ ∆OAM cân tại O \( \Rightarrow \widehat {OAM} = \widehat {OMA}\)
Mà \[\widehat {OAM} + \widehat {SAM} = \widehat {SAO} = 90^\circ \] và \[\widehat {AMH} + \widehat {HAM} = 90^\circ \] (∆HAM vuông tại H)
\( \Rightarrow \widehat {SAM} = \widehat {HAM}\)
Þ AM là đường phân giác của ∆SAD (1)
Mặt khác SA, SD là các tiếp tuyến của đường tròn (O)
Þ SO là tia phân giác của \[\widehat {ASD}\]
Þ SO là đường phân giác của ∆SAD (2)
Từ (1) và (2) Þ M là tâm đường tròn nội tiếp ∆SAD
Mà MH ^ AD tại H Þ MH là bán kính đường tròn nội tiếp ∆SAD
Þ MH = r Þ OH = R − r
Áp dụng định lí Py-ta-go vào ∆AOH vuông tại H, ta có:
\(AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \)
\[ \Rightarrow AD = 2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \]
Ta có \(\widehat {EAD}\) chắn đường kính DE suy ra \[\widehat {EAD} = 90^\circ \].
Áp dụng định lí Py-ta-go vào ∆EAD vuông tại A, ta có:
\(AE = \sqrt {D{E^2} - A{D^2}} = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} } \right)}^2}} = 2\left( {R - r} \right)\)
3) OH là đường trung trực của AD, M Î OH Þ DM = AM = R
Tứ giác AMDO có AM = MD = OA = OD (=R)
ÞTứ giác AMDO là hình thoi
ÞAM // OD. Mà AM ^ BMÞ BM ^ OD
∆OMD có OM = OD = CD (=R) Þ ∆OMD đều
Mà MB, DM là hai đường cao cắt nhau tại K của ∆OMD
Do đó K là trực tâm của tam giác đều OMD
Þ K là trọng tâm của tam giác đều OMD
\[ \Rightarrow KH = \frac{1}{3}DH,\;KD = \frac{2}{3}DH \Rightarrow KH\,.\,KD = \frac{2}{9}D{H^2}\]
Mà ∆HMD vuông tại H
\[ \Rightarrow DH = MD\,.\,\sin \widehat {HMD} = MD\,.\,\sin 60^\circ = \frac{{\sqrt 3 }}{2}MD\]
\( \Rightarrow MD = \frac{2}{{\sqrt 3 }}DH\)
\( \Rightarrow M{D^2} = \frac{4}{3}D{H^2} = 6\,.\,\frac{2}{9}D{H^2} = 6KH\,.\,KD\)
\( \Rightarrow \frac{{M{D^2}}}{6} = KH\,.\,KD\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1,2,3.
Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1,2,3 luôn đứng cạnh nhau.
Thửa ruộng hình chữ nhật có chiều dài 60 m, chiều rộng bằng \(\frac{2}{3}\) chiều dài. Trung bình cứ 100 mét vuông thì thu hoạch được 50 kg thóc. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu ki-lô-gam thóc?
Tìm m để bất phương trình 2x2 − (2m + 1)x + m2 − 2m + 2 ≤ 0 nghiệm đúng với mọi \[x \in \left[ {\frac{1}{2};\;2} \right]\]
Tìm m để mọi x Î [0; +∞) đều là nghiệm của bất phương trình:
(m2 − 1)x2 − 8mx + 9 − m2 ≥ 0
Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)
Tìm m để đồ thị hàm số bậc nhất y = mx − 4 cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5.
Một thửa ruộng hình chữ nhật có chiều dài 60m, chiều dài bằng \(\frac{3}{2}\) chiều rộng, trên thửa ruộng đó người ta trồng lúa cứ 100m2 thu hoạch được 50 kg. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ thóc?
Tam giác ABC vuông tại A, AB = a, AC = 3a.Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách.
Cho (O) và (O') cắt nhau tại A và B. Vẽ hình bình hành OBO'C.
Chứngminh: AC//OO'
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB).Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
b) Vẽ MH ^ OI tại H. Chứng minh OB2 = OH.OI.
c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.
Thiết diện đi qua trục của hình nón đỉnh S là tam giác vuông cân SAB có cạnh cạnh huyền bằng \[a\sqrt 2 \]. Diện tích toàn phần Stp của hình nón và thể tích V của khối nón tương ứng đã cho là bao nhiêu?
Cho 2 số dương x, y thay đổi thỏa mãn xy = 2. Tìm GTNN của biểu thức:\(M = \frac{1}{x} + \frac{2}{y} + \frac{3}{{2x + y}}\).
Cho đoạn thẳng AB. Xác định vị trí của điểm C trên đoạn thẳng AB sao cho CA ≤ CB.
Cho phương trình: x2 − (m − 2)x− m − 1 = 0 (với m là tham số)
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt x1, x2 với mọi m.
b) Tìm m thỏa mãn hệ thức: (x1 − x2)2 − 3x1x2 = 21
Cho số phức z thỏa mãn |z + i + 1| = |z − 2i|. Tìm giá trị nhỏ nhất |z|.