Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 76)
-
1332 lượt thi
-
85 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.
 Xem đáp án
Xem đáp án
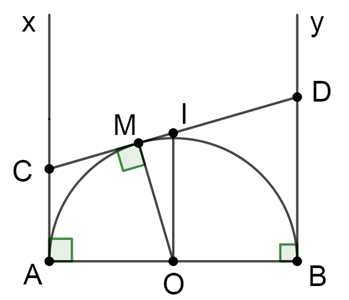
Theo tính chất tiếp tuyến, ta có: Ax ^ AB; By ^ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC Þ OI ^ AB
Vì OC và OD lần lượt là phân giác của \[\widehat {AOM}\] và \[\widehat {BOM}\] nên:
OC ^ OD (tính chất hai góc kề bù) \( \Rightarrow \widehat {COD} = 90^\circ \)
Suy ra: \(IC = ID = IO = \frac{1}{2}CD\) (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD.Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.
Câu 2:
Biết đồ thị hàm số y = (k − 3)x − 4 cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5. Tìm tham số k
 Xem đáp án
Xem đáp án
A là điểm có tung độ bằng 5 và A thuộc đường thẳng y = −3x + 2 nên ta có:
5 = −3x + 2 Û x = −1
Suy ra A(−1; 5) thuộc đường thẳng y = (k − 3)x – 4 nên ta có:
5 = (k − 3)(−1) – 4 ⇔ k = −6
Vậy k = −6 là giá trị cần tìm.
Câu 3:
Tìm m để đồ thị hàm số bậc nhất y = mx − 4 cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5.
 Xem đáp án
Xem đáp án
A là điểm có tung độ bằng 5 và A thuộc đường thẳng y = −3x+2 nên ta có:
5 = −3x+2 Û x = −1
Suy ra A(−1; 5) thuộc đường thẳngy = mx − 4 nên ta có:
5 = m(−1) – 4 Û m = −9
Vậy m = −9 là giá trị cần tìm.
Câu 4:
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB).Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
b) Vẽ MH ^ OI tại H. Chứng minh OB2 = OH.OI.
c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.
 Xem đáp án
Xem đáp án
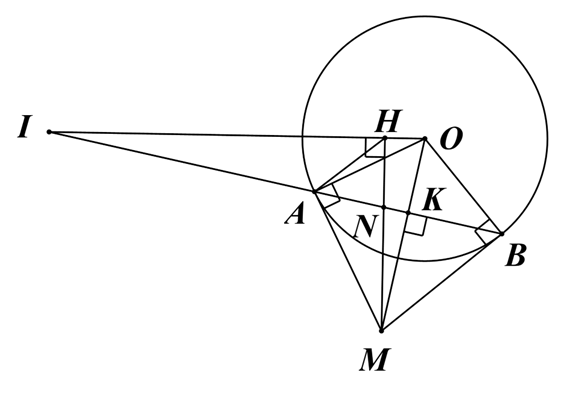
a) Ta có MA, MB là hai tiếp tuyến của (O) cắt nhau tại M.
Suy ra MA = MB.
Khi đó M nằm trên đường trung trực của đoạn thẳng AB (1)
Lại có OA = OB =R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AB (2)
Từ (1), (2), suy ra MO là đường trung trực của đoạn thẳng AB.
Do đó MO ^ AB tại K và K là trung điểm AB.
b) Xét ∆OHM và ∆OKI, có:
\(\widehat O\) chung.
\[\widehat {OHM} = \widehat {OKI} = 90^\circ \]
Do đó ∆OHM ᔕ ∆OKI (g.g).
Suy ra \(\frac{{OH}}{{OK}} = \frac{{OM}}{{OI}}\).
Do đó OH.OI = OM.OK.
Xét ∆AOM vuông tại A có AK là đường cao:
OA2 = OK.OM (hệ thức lượng trong tam giác vuông).
Vậy OH.OI = OA2 = OB2 (điều phải chứng minh).
c) Ta có \[\widehat {OAM} = 90^\circ \;\left( {gt} \right)\]
Suy ra O, A, M nội tiếp đường tròn đường kính OM.
Tương tự, ta có O, H, M nội tiếp đường tròn đường kính OM.
Khi đó tứ giác AHOM nội tiếp đường tròn đường kính OM.
Suy ra \(\widehat {AMO} = \widehat {AHI}\)(1)
Ta có \[\widehat {OAM} = \widehat {OBM} = 90^\circ \](MA, MB là các tiếp tuyến của đường tròn (O)).
Suy ra \[\widehat {OAM} + \widehat {OBM} = 180^\circ \]
Do đó tứ giác OAMB nội tiếp đường tròn đường kính OM.
Vì \[\widehat {AMO} = \widehat {ABO}\](cùng chắn cung ) (2)
Từ (1), (2), suy ra \[\widehat {ABO} = \widehat {AHI}\]
Xét ∆IHN và ∆IKO, có:
\[\widehat I\] chung.
\[\widehat {IHN} = \widehat {IKO} = 90^\circ \]
Do đó ∆IHN ᔕ ∆IKO (g.g).
Suy ra \(\frac{{IH}}{{IK}} = \frac{{IN}}{{IO}}\)
Do đó IH.IO = IN.IK (3)
Xét ∆AHI và ∆OBI, có:
\[\widehat I\]chung.
\[\widehat {ABO} = \widehat {AHI}\](chứng minh trên).
Do đó ∆AHI ᔕ ∆OBI (g.g).
Suy ra \[\frac{{IA}}{{IO}} = \frac{{IH}}{{IB}}\].
Do đó IA.IB = IH.IO (4)
Từ (3), (4), suy ra IA.IB = IN.IK (điều phải chứng minh).
Câu 5:
Tìm m để bất phương trình 2x2 − (2m + 1)x + m2 − 2m + 2 ≤ 0 nghiệm đúng với mọi \[x \in \left[ {\frac{1}{2};\;2} \right]\]
 Xem đáp án
Xem đáp án
Đặt f(x) =2x2 − (2m + 1)x + m2 − 2m + 2
Xét ∆ = −4m2 + 20m − 15
+) Nếu \(\Delta \le 0 \Leftrightarrow \left[ \begin{array}{l}m \le \frac{{5 - \sqrt {10} }}{2}\\m \ge \frac{{5 + \sqrt {10} }}{2}\end{array} \right.\)
Suy ra f(x) ≥ 0 với mọi x (loại)
+) Nếu \(\Delta > 0 \Leftrightarrow m \in \left( {\frac{{5 - \sqrt {10} }}{2};\;\frac{{5 + \sqrt {10} }}{2}} \right)\)
Khi đó f(x) có hai nghiệm
\({x_1} = \frac{{2m + 1 - \sqrt \Delta }}{4},\;{x_2} = \frac{{2m + 1 + \sqrt \Delta }}{4}\;\left( {{x_1} < {x_2}} \right)\;\)
Và f(x) ≤ 0 khi x1 ≤ x ≤ x2
Do đó yêu cầu bài toán
\( \Leftrightarrow \left\{ \begin{array}{l}{x_1} \le \frac{1}{2}\\{x_2} \ge 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \le 2\sqrt \Delta \\7 - 2m \le \sqrt \Delta \end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 1} \right)^2} \le 4\Delta \\{\left( {7 - 2m} \right)^2} \le \Delta \\\frac{1}{2} \le m \le \frac{7}{2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}20{m^2} - 84m = 61 \le 0\\{m^2} - 6m + 8 \le 0\\\frac{1}{2} \le m \le \frac{7}{2}\end{array} \right.\)
\( \Leftrightarrow 2 \le m \le \frac{{21 + 2\sqrt {34} }}{{10}}\)
Vậy \(2 \le m \le \frac{{21 + 2\sqrt {34} }}{{10}}\).
Câu 6:
Cho phương trình: x2 − (m − 2)x− m − 1 = 0 (với m là tham số)
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt x1, x2 với mọi m.
b) Tìm m thỏa mãn hệ thức: (x1 − x2)2 − 3x1x2 = 21
 Xem đáp án
Xem đáp án
x2 − (m − 2)x − m − 1 = 0
Δ=(m−2)2+4m+ 4 =m2+8> 0, ∀m
Þ Phương trình luôn có 2 nghiệm phân biệt
Theo Viet ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 2\\{x_1}{x_2} = - m - 1\end{array} \right.\)
(x1−x2)2−3x1x2= 21
Û(x1+x2)2− 7x1x2− 21 = 0
Û(m−2)2+7m+7− 21 =0
Ûm2+3m− 10 =0
\( \Rightarrow \left[ \begin{array}{l}m = 2\\m = - 5\end{array} \right.\)
Vậy m = 2 và m =−5 là các giá trị thỏa mãn.
Câu 7:
Cho hai hàm số y=x2 và y=2x − m+2.Tìm m để đồ thị hai hàm số trên chỉ có một điểm chung? Tìm tọa độ điểm chung đó?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm là:
x2 = 2x − m + 2
Û x2 − 2x + m − 2 = 0
Để hai đồ thị hàm số chỉ có một điểm chung thì Δ¢ = 0
Û 1 − m + 2 = 0 Û m = 3
Vậy hoành độ giao điểm đó là nghiệm của phương trình
x2 − 2x + 1 = 0 Û x = 1
Þ y = 1
Vậy tọa độ điểm chung đó là (1; 1).
Câu 8:
Cho tam giác ABC cân (AB = AC). Gọi H là trung điểm của cạnh BC, D là hình chiếu vuông góc của H trên cạnh AC, M là trung điểm của đoạn HD. Chứng minh rằng AM vuông góc với BD.
 Xem đáp án
Xem đáp án
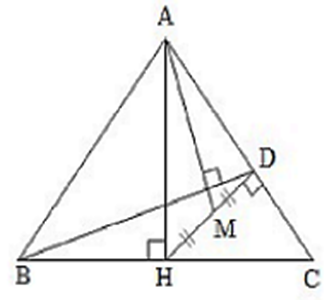
Ta chứng minh: \(\overrightarrow {AM} \,.\,\overrightarrow {DB} = 0\)
Ta có: \[\overrightarrow {BD} = \overrightarrow {BH} + \overrightarrow {HD} = \overrightarrow {HC} + \overrightarrow {HD} \]
\(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AH} + \overrightarrow {AD} } \right)\)
Do đó: \(\overrightarrow {AM} \,.\,\overrightarrow {DB} = \frac{1}{2}\left( {\overrightarrow {AH} + \overrightarrow {AD} } \right)\left( {\overrightarrow {HC} + \overrightarrow {HD} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AH} \,.\,\overrightarrow {HC} + \overrightarrow {AH} \,.\,\overrightarrow {HD} + \overrightarrow {AD} \,.\,\overrightarrow {HC} + \overrightarrow {AD} \,.\,\overrightarrow {HD} } \right)\)
Mà: \(\left\{ \begin{array}{l}\overrightarrow {AH} \,.\,\overrightarrow {HC} = 0\;\left( {do\;AH \bot BC} \right)\\\overrightarrow {AD} \,.\,\overrightarrow {HD} = 0\;\left( {do\;AC \bot HD} \right)\end{array} \right.\)
Do đó: \(\overrightarrow {AM} \,.\,\overrightarrow {DB} = \frac{1}{2}\left( {\overrightarrow {AH} \,.\,\overrightarrow {HD} + \overrightarrow {AD} \,.\,\overrightarrow {HC} } \right)\)
\( = \frac{1}{2}\left[ {\overrightarrow {AH} \,.\,\overrightarrow {HD} + \left( {\overrightarrow {AH} + \overrightarrow {HD} } \right)\,.\,\overrightarrow {HC} } \right]\)
\( = \frac{1}{2}\left( {\overrightarrow {AH} \,.\,\overrightarrow {HD} + \overrightarrow {HD} \,.\,\overrightarrow {HC} } \right)\)vì\(\overrightarrow {AH} \,.\,\overrightarrow {HC} = 0\)
\(\overrightarrow {AM} \,.\,\overrightarrow {DB} = \frac{1}{2}\overrightarrow {HD} \left( {\overrightarrow {AH} + \,\overrightarrow {HC} } \right) = \frac{1}{2}\overrightarrow {HD} \,.\,\overrightarrow {AC} = 0\) (vì AC ^ HD)
Vậy AM ^ DB.
Câu 9:
Cho hàm số y = −x3 + (2m + 1)x2 − (m2 − 3m + 2)x − 4 (Cm). (Với m là tham số)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
b) Tìm m để đồ thị hàm số (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.
 Xem đáp án
Xem đáp án
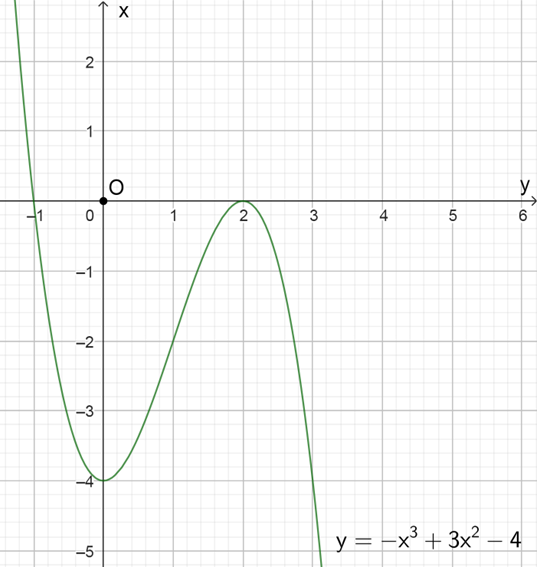
a) Với m = 1 ta có: y = −x3 + 3x2 − 4 (Cm)
TXĐ: D =ℝ
\[{\lim _{x \to \pm \infty }}y = \pm \infty \]
\(y' = - 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Bảng biến thiên
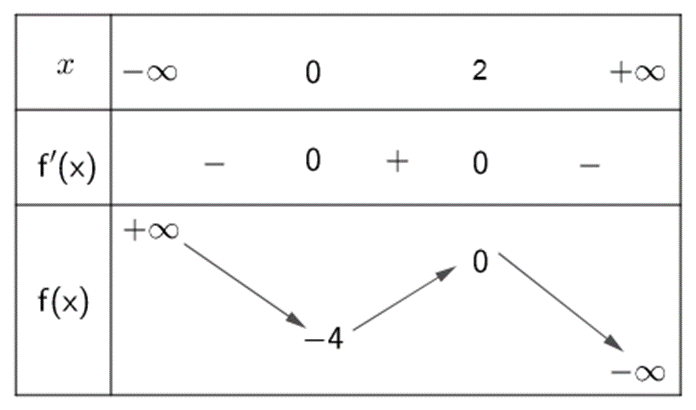
Đồ thị hàm số nhận (1; −2) làm tâm đối xứng và đi qua hai điểm (0; −4) và (2; 0).
b) Ta có: y¢ = −3x2 + 2(2m + 1)x − (m2 − 3m + 2)
Để hàm số có các điểm cực đại và cực tiểu nằm về hai phía của trục tung khi y¢ = 0 có hai nghiệm trái dấu.
Suy ra m2 − 3m + 2 < 0 Û 1 < m < 2
Vậy m Î (1; 2)
Câu 10:
Tìm các giá trị của m sao cho đồ thị hàm số \(y = \frac{1}{3}{x^3} + m{x^2} - \left( {6m + 9} \right)x - 12\) có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục tung.
 Xem đáp án
Xem đáp án
TXĐ: D =ℝ
Ta có y¢ = x2 + 2mx − (6m + 9)
Để hàm số có các điểm cực đại và cực tiểu nằm cùng một phía đối với trục tung khi và chỉ khi phương trình y¢ = 0 có hai nghiệm phân biệt x1, x2 thỏa mãn x1x2 > 0
\[ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} + 6m + 9 > 0\\ - 6m - 9 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m < \frac{{ - 3}}{2}\end{array} \right.\]
Vậy \( - 3 \ne m < \frac{{ - 3}}{2}\) là các giá trị của m thỏa mãn.
Câu 11:
Một cửa hàng bán vải được 2 160 000 đồng tính ra được lãi 160 000 đồng . Hỏi số tiền lãi bằng bao nhiêu phần trăm tiền vốn?
 Xem đáp án
Xem đáp án
Số tiền vốn là:
2160000 − 160000 = 2 000 000 (đồng)
Tỉ số phần trăm tiền lãi với tiền vốn là:
160 000 : 2 000 000 × 100 = 8%
Đáp số: 8%.
Câu 12:
Một cửa hàng bán vải được 2 160 000 đồng. Tính gia cửa hàng lãi 8% so với tiền vốn. Hỏi số tiền lãi là bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Tiền bán ứng:
100% + 8% = 108%
Tiền vốn là:
2160 000 : 108% = 2000 000 (đồng )
Tiền lãi là:
2160 000 − 2000 000 = 160 000 (đồng )
Đáp số: 160 000 đồng.
Câu 13:
Cho hình chóp S.ABCD có đáy là hình hình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây:
a) (SAC) và (SBD);
b) (SAB) và (SCD);
c) (SAD) và (SBC).
 Xem đáp án
Xem đáp án
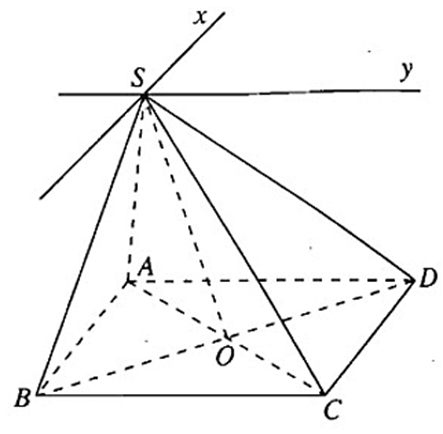
a) Ta có: \(\left\{ \begin{array}{l}S \in \left( {SAC} \right)\\S \in \left( {SBD} \right)\end{array} \right. \Rightarrow S \in \left( {SAD} \right) \cap \left( {SBD} \right)\)
Gỉa sử AC Ç BD = O \( \Rightarrow \left\{ \begin{array}{l}O \in \left( {SAC} \right)\\O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAD} \right) \cap \left( {SBD} \right)\)
Þ (SAD) Ç (SBD) = SO
b) Ta có:
\(\left\{ \begin{array}{l}S \in \left( {SAC} \right)\\S \in \left( {SCD} \right)\end{array} \right. \Rightarrow S \in \left( {SAD} \right) \cap \left( {SCD} \right)\)
Ta lại có:
\(\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\CD \subset \left( {SCD} \right)\\AB\;{\rm{//}}\;CD\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = Sx\)và Sx // AB // CD
c) Lập luận tương tự câu b ta có:
(SAD) Ç (SBC) = Sy và Sy // AD // BC.
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao tuyến của (SAC) và (SBD).
b) Tìm giao điểm DN với (SAC).
c) Chứng minh: MN // (SCD).
 Xem đáp án
Xem đáp án
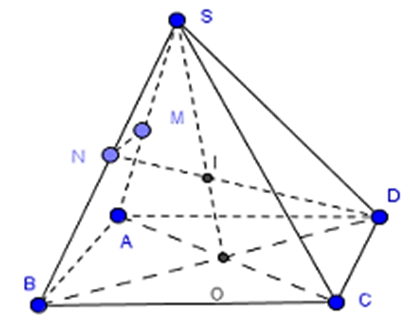
a) Ta có:
\(\left\{ \begin{array}{l}S \in \left( {SAC} \right)\\S \in \left( {SBD} \right)\end{array} \right. \Rightarrow S \in \left( {SAD} \right) \cap \left( {SBD} \right)\)
Gỉả sử AC Ç BD = O \( \Rightarrow \left\{ \begin{array}{l}O \in \left( {SAC} \right)\\O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAD} \right) \cap \left( {SBD} \right)\)
Þ (SAD) Ç (SBD) = SO
b) DN Ì (SBD)
Mà SO =(SAC) Ç (SBD)
Gọi SO Ç DN = I
Suy ra I = DN ∩ (SAC)
c) Ta có: MN // AB (tính chất đường trung bình trong tam giác SAB)
Mà AB // CD (ABCD là hình bình hành)
Suy ra MN // CD
Mặt khác CDÌ(SCD)
Do đó MN // (SCD).
Câu 15:
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1) Chứng minh: SD là tiếp tuyến của đường tròn (O).
2) Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3) Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH\,.\,KD\).
 Xem đáp án
Xem đáp án
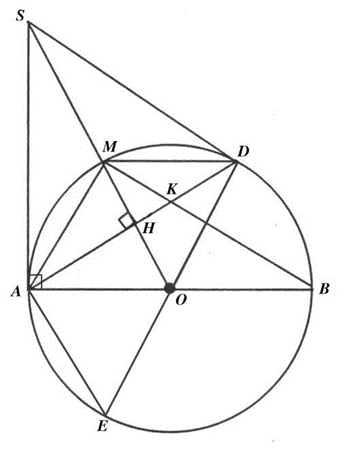
1) Xét ∆OAB có \(\left\{ \begin{array}{l}OA = OD = R\\OH \bot AD\end{array} \right.\)
Þ ∆OAD cân tại O có OH là đường cao
Þ OH là đường phân giác của \(\widehat {AOD}\)
\[ \Rightarrow \widehat {AOH} = \widehat {DOH}\]hay\[\widehat {AOS} = \widehat {DOS}\]
Xét ∆SAO và ∆SDO có:
KO chung
\[\widehat {AOS} = \widehat {DOS}\]
OA = OD = R
Do đó ∆SAO = ∆SDO (c.g.c)
Mà \(\widehat {SAO} = 90^\circ \) (SA ^ OA do SA là tiếp tuyến của (O) tại A)
\( \Rightarrow \widehat {SDO} = 90^\circ \)hay SD ^ OD
Suy ra SD là tiếp tuyến của (O) tại D.
2) ∆OAM có OA = OM = R
Þ ∆OAM cân tại O \( \Rightarrow \widehat {OAM} = \widehat {OMA}\)
Mà \[\widehat {OAM} + \widehat {SAM} = \widehat {SAO} = 90^\circ \] và \[\widehat {AMH} + \widehat {HAM} = 90^\circ \] (∆HAM vuông tại H)
\( \Rightarrow \widehat {SAM} = \widehat {HAM}\)
Þ AM là đường phân giác của ∆SAD (1)
Mặt khác SA, SD là các tiếp tuyến của đường tròn (O)
Þ SO là tia phân giác của \[\widehat {ASD}\]
Þ SO là đường phân giác của ∆SAD (2)
Từ (1) và (2) Þ M là tâm đường tròn nội tiếp ∆SAD
Mà MH ^ AD tại H Þ MH là bán kính đường tròn nội tiếp ∆SAD
Þ MH = r Þ OH = R − r
Áp dụng định lí Py-ta-go vào ∆AOH vuông tại H, ta có:
\(AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \)
\[ \Rightarrow AD = 2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \]
Ta có \(\widehat {EAD}\) chắn đường kính DE suy ra \[\widehat {EAD} = 90^\circ \].
Áp dụng định lí Py-ta-go vào ∆EAD vuông tại A, ta có:
\(AE = \sqrt {D{E^2} - A{D^2}} = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} } \right)}^2}} = 2\left( {R - r} \right)\)
3) OH là đường trung trực của AD, M Î OH Þ DM = AM = R
Tứ giác AMDO có AM = MD = OA = OD (=R)
ÞTứ giác AMDO là hình thoi
ÞAM // OD. Mà AM ^ BMÞ BM ^ OD
∆OMD có OM = OD = CD (=R) Þ ∆OMD đều
Mà MB, DM là hai đường cao cắt nhau tại K của ∆OMD
Do đó K là trực tâm của tam giác đều OMD
Þ K là trọng tâm của tam giác đều OMD
\[ \Rightarrow KH = \frac{1}{3}DH,\;KD = \frac{2}{3}DH \Rightarrow KH\,.\,KD = \frac{2}{9}D{H^2}\]
Mà ∆HMD vuông tại H
\[ \Rightarrow DH = MD\,.\,\sin \widehat {HMD} = MD\,.\,\sin 60^\circ = \frac{{\sqrt 3 }}{2}MD\]
\( \Rightarrow MD = \frac{2}{{\sqrt 3 }}DH\)
\( \Rightarrow M{D^2} = \frac{4}{3}D{H^2} = 6\,.\,\frac{2}{9}D{H^2} = 6KH\,.\,KD\)
\( \Rightarrow \frac{{M{D^2}}}{6} = KH\,.\,KD\).
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD.Mặt bên (SAB) tạo với đáy một góc bằng 60°.Tính theo a khoảng cách từ B đến mặt phẳng (SAD).
 Xem đáp án
Xem đáp án
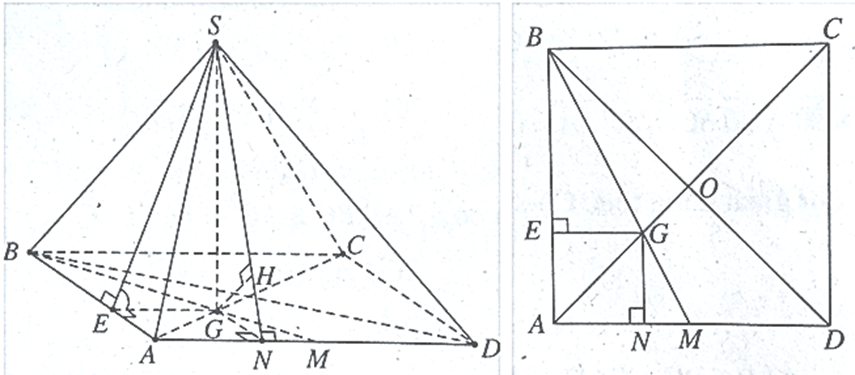
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
AB ^ SG và AB ^ GEÞ AB ^ (SEG) Þ AB ^ SE.
SE ^ AB và GE ^AB\(\left( {\widehat {\left( {SAB} \right)\,,\,\left( {ABCD} \right)}} \right) = \widehat {SEG} = 60^\circ \)
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ^ AD. Tương tự như trên, ta có: AD ^ GN và AD ^ SGÞ AD ^ (SGN)
Hạ GH ^ SN, ta có GH ^ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
Trong tam giác vuông SGN, ta có: \(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}}\) (1)
Do GN // AB nên \(\frac{{GN}}{{BA}} = \frac{{MG}}{{MB}} = \frac{1}{3}\)
Ta có: \[GN = \frac{{BA}}{3} = \frac{a}{3}\]
Trong tam giác SGE, ta được \(GS = GE\,.\,\tan 60^\circ = \frac{{a\sqrt 3 }}{3}\) (Do GE = GN)
Thế vào (1) ta được:
\(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{a}{3}} \right)}^2}}} = \frac{{36}}{{3{a^2}}}\)
\( \Rightarrow GH = \frac{{a\sqrt 3 }}{6}\)
Ta có: M Î(SAD) và MB= 3MG
\( \Rightarrow d\left( {B,\;\left( {SAD} \right)} \right) = 3d\left( {G,\;\left( {SAD} \right)} \right) = 3\,.\,\frac{{a\sqrt 3 }}{6} = \frac{{a\sqrt 3 }}{2}\).
Câu 17:
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H trùng với trung điểm của AB, biết\(SH = a\sqrt 3 \). Gọi M là giao điểm của HD và AC. Tính khoảng cách từ điểm M đến mặt phẳng (SCD).
 Xem đáp án
Xem đáp án
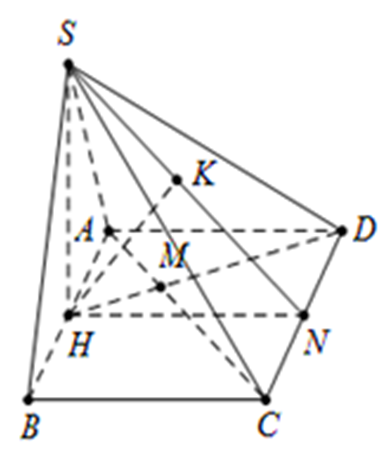
Xét ∆HAD, có AC là tia phân giác của góc \(\widehat {HAD}\)
\[ \Rightarrow \frac{{AH}}{{AD}} = \frac{{HM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{HD}}{{MD}} = \frac{3}{2}\]
Ta có: \(\left\{ \begin{array}{l}H,\;M \in HD\\HM \cap \left( {SCD} \right) = D\end{array} \right. \Rightarrow \frac{{d\left( {H,\;\left( {SCD} \right)} \right)}}{{d\left( {M,\;\left( {SCD} \right)} \right)}} = \frac{{HD}}{{MD}} = \frac{3}{2}\)
Gọi N là trung điểm của CD Þ HN ^ CD
Trong (SHN) từ H kẻ HK ^ SN (1), K Î SN
Ta có: \(\left\{ \begin{array}{l}CD \bot HN\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHN} \right) \Rightarrow CD \bot HK\;\left( 2 \right)\)
Từ (1) và (2) Þ HK ^ (SCD)
Khi đó: \(d\left( {H,\;\left( {SCD} \right)} \right) = HK = \frac{{SH\,.\,HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \frac{{a\sqrt 3 \,.\,a}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}} }} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow d\left( {M,\;\left( {SCD} \right)} \right) = \frac{{a\sqrt 3 }}{2}:\frac{3}{2} = \frac{a}{{\sqrt 3 }}\)
Câu 18:
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2, diện tích tam giác A’BC bằng 3. Tính thể tích của khối lăng trụ.
 Xem đáp án
Xem đáp án
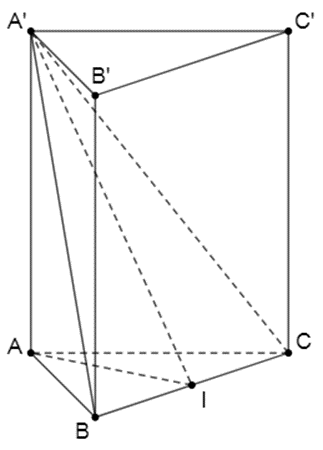
Gọi I là trung điểm của BC ta có:
\(\left\{ \begin{array}{l}BC \bot AI\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot A'I\)
Lại có: \({S_{A'BC}} = \frac{1}{2}A'I\,.\,BC \Rightarrow A'I = \frac{6}{{BC}} = 3\)
Mặt khác \(AI = \frac{{AB\sqrt 3 }}{2} = \sqrt 3 \)
\( \Rightarrow AA' = \sqrt {A'{I^2} - A{I^2}} = \sqrt 6 \)
Khi đó \({S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \sqrt 3 \)
Suy ra \(V = AA'\,.\,{S_{ABC}} = \sqrt 6 \,.\,\sqrt 3 = 3\sqrt 2 \)
Câu 19:
Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, diện tích mặt bên ABB’A’ bằng 2a2. Tính thể tích V của khối lăng trụ ABC.A’B’C’
 Xem đáp án
Xem đáp án
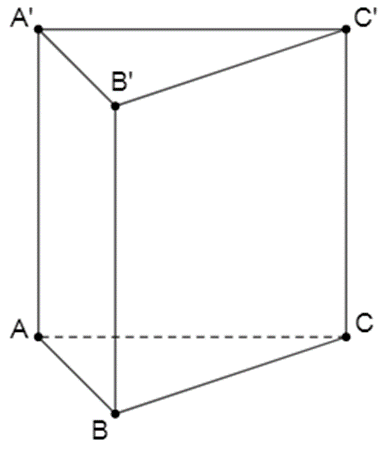
Ta có: \({S_{ABB'A'}} = AB\,.\,AA' = 2{a^2} \Rightarrow AA' = \frac{{2{a^2}}}{a} = 2a\).
\({S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\).
Suy ra\(V = AA'\,.\,{S_{ABC}} = 2a\,.\,\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{2}\).
Câu 20:
Thiết diện đi qua trục của hình nón đỉnh S là tam giác vuông cân SAB có cạnh cạnh huyền bằng \[a\sqrt 2 \]. Diện tích toàn phần Stp của hình nón và thể tích V của khối nón tương ứng đã cho là bao nhiêu?
 Xem đáp án
Xem đáp án

+ Do thiết diện đi qua trục là tam giác SAB vuông cân tại đỉnh S, có cạnh huyền \[AB = a\sqrt 2 \] nên suy ra bán kính đáy hình nón là \[r = \frac{{a\sqrt 2 }}{2}\]; đường sinh hình nón l = SA = SB = a; đường cao hình nón \(h = SO = \frac{{a\sqrt 2 }}{2}\).
+ Diện tích toàn phần hình nón là:
(đvdt).
+ Thể tích khối nón tương ứng là:
\(V = \frac{1}{3}B\,.\,h = \frac{1}{3}\pi {r^2}\,.\,h = \frac{1}{3}\pi {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}\,.\,\left( {\frac{{a\sqrt 2 }}{2}} \right) = \frac{{\pi {a^3}\sqrt 2 }}{{12}}\)(đvtt).
Câu 21:
Cho hình nón đỉnh S có đường cao SO = a. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 2 }}{2}\). Diện tích xung quanh của hình nón đã cho bằng
 Xem đáp án
Xem đáp án
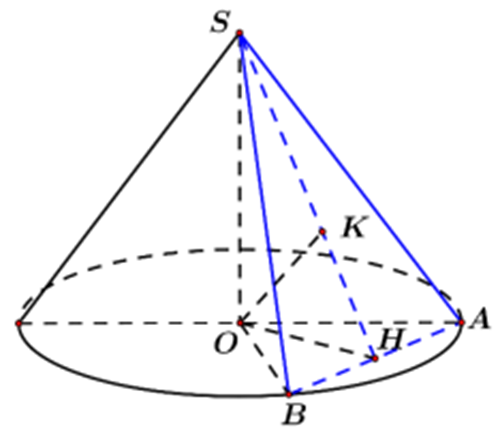
Gọi H, K lần lượt là hình chiếu của O lên AB và SH.
Ta có: AB ^ (SOH) Þ AB ^ OK
Mà OK ^ SH nên OK ^ (SAB)
\( \Rightarrow OK = d\left( {O,\;\left( {SAB} \right)} \right) = \frac{{a\sqrt 2 }}{2}\)
Trong tam giác vuông SOH, ta có:
\(\frac{1}{{O{K^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{H^2}}} \Leftrightarrow \frac{1}{{O{H^2}}} = \frac{1}{{O{K^2}}} - \frac{1}{{O{S^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}} - \frac{1}{{{a^2}}} = \frac{1}{{{a^2}}}\)
Þ OH = a
Khi đó: \(SH = \sqrt {S{O^2} + O{H^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Vì tam giác SAB vuông cân tại S nên có
\(SH = \frac{{AB}}{2} \Rightarrow AB = 2SH = 2a\sqrt 2 \)
Khi đó độ dài đường sinh là
l = SA = SB = 2a
Bán kính của đường tròn đáy là
\(r = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 2 }}{2}} \right)}^2}} = a\sqrt 3 \)
Vậy diện tích xung quanh của hình nón là
\[{S_{xq}} = \pi \,.\,r\,.\,l = \pi \,.\,a\sqrt 3 .\,2a = 2\pi {a^2}\sqrt 3 \].
Câu 22:
Cho các số dương x, y, z thoả mãn x + y + z = 3. Tìm GTLN của
\(B = \sqrt {\frac{{xy}}{{xy + 3z}}} + \sqrt {\frac{{yz}}{{yz + 3x}}} + \sqrt {\frac{{zx}}{{zx + 3y}}} \).
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức AM - GM và kết hợp với giả thiết x + y + z = 3, ta có:
\[B = \sqrt {\frac{{xy}}{{xy + 3z}}} + \sqrt {\frac{{yz}}{{yz + 3x}}} + \sqrt {\frac{{zx}}{{zx + 3y}}} \]
\( = \sqrt {\frac{{xy}}{{xy + \left( {x + y + z} \right)z}}} + \sqrt {\frac{{yz}}{{yz + \left( {x + y + z} \right)x}}} + \sqrt {\frac{{zx}}{{zx + \left( {x + y + z} \right)y}}} \)
\( = \sqrt {\frac{{xy}}{{\left( {x + z} \right)\left( {y + z} \right)}}} + \sqrt {\frac{{yz}}{{\left( {y + x} \right)\left( {z + x} \right)}}} + \sqrt {\frac{{zx}}{{\left( {z + y} \right)\left( {x + y} \right)}}} \)
\( \le \frac{1}{2}\left( {\frac{x}{{x + z}} + \frac{y}{{y + z}} + \frac{y}{{y + x}} + \frac{z}{{z + x}} + \frac{z}{{z + y}} + \frac{x}{{x + y}}} \right)\)
\[ = \frac{1}{2}.\left( {\frac{{x + z}}{{x + z}} + \frac{{y + z}}{{y + z}} + \frac{{x + y}}{{x + y}}} \right) = \frac{3}{2}\]
Dấu “=” xảy ra khi và chỉ khi x = y = z = 1.
Vậy GTLN của B bằng \(\frac{3}{2}\) khi x = y = z = 1.
Câu 23:
Cho x, y,z là ba số dương thoả mãn x + y + z = 3. Chứng minh:
\(\frac{x}{{x + \sqrt {3x + yz} }} + \frac{y}{{y + \sqrt {3y + zx} }} + \frac{z}{{z + \sqrt {3z + xy} }} \le 1\).
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức Bunhiacốpxki và kết hợp với giả thiết x + y + z = 3, ta có:
\(\frac{x}{{x + \sqrt {3x + yz} }} + \frac{y}{{y + \sqrt {3y + zx} }} + \frac{z}{{z + \sqrt {3z + xy} }}\)
\( = \frac{x}{{x + \sqrt {x\left( {x + y + z} \right) + yz} }} + \frac{y}{{y + \sqrt {\left( {x + y + z} \right)y + zx} }} + \frac{z}{{z + \sqrt {\left( {x + y + z} \right)z + xy} }}\)
\[ = \frac{x}{{x + \sqrt {\left( {x + y} \right)\left( {x + z} \right)} }} + \frac{y}{{y + \sqrt {\left( {y + z} \right)\left( {y + x} \right)} }} + \frac{z}{{z + \sqrt {\left( {z + x} \right)\left( {z + y} \right)} }}\]
\( \le \frac{x}{{x + \sqrt {{{\left( {\sqrt {xy} + \sqrt {xz} } \right)}^2}} }} + \frac{y}{{y + \sqrt {{{\left( {\sqrt {xy} + \sqrt {yz} } \right)}^2}} }} + \frac{z}{{z + \sqrt {{{\left( {\sqrt {xz} + \sqrt {yz} } \right)}^2}} }}\)
\[ = \frac{x}{{x + \sqrt {xy} + \sqrt {xz} }} + \frac{y}{{y + \sqrt {xy} + \sqrt {yz} }} + \frac{z}{{z + \sqrt {xz} + \sqrt {yz} }}\]
\[ = \frac{{\sqrt x }}{{\sqrt x + \sqrt y + \sqrt z }} + \frac{{\sqrt y }}{{\sqrt x + \sqrt y + \sqrt z }} + \frac{{\sqrt z }}{{\sqrt x + \sqrt y + \sqrt z }}\]
\[ = \frac{{\sqrt x + \sqrt y + \sqrt z }}{{\sqrt x + \sqrt y + \sqrt z }} = 1\].
Vậy \(\frac{x}{{x + \sqrt {3x + yz} }} + \frac{y}{{y + \sqrt {3y + zx} }} + \frac{z}{{z + \sqrt {3z + xy} }} \le 1\) (đpcm)
Câu 24:
Tìm x biết |x − 1| = 3x + 2.
 Xem đáp án
Xem đáp án
|x − 1| = 3x + 2
• TH1: x − 1 ≥ 0 Û x ≥ 1
x − 1 = 3x + 2
Û 3x − x = −1 − 2
Û 2x = −3
\( \Rightarrow x = - \frac{3}{2}\) (loại)
• TH2: x − 1 < 0 Û x < 1
−x + 1 = 3x + 2
Û 3x + x = 1 − 2
Û 4x = −1
\( \Rightarrow x = - \frac{1}{4}\) (thỏa mãn)
Vậy \(x = - \frac{1}{4}\) là nghiệm của phương trình.
Câu 25:
Giải phương trình: |x − 1| − 3x = 2.
 Xem đáp án
Xem đáp án
|x − 1| − 3x = 2
Û|x − 1| = 2 + 3x
• TH1: x − 1 ≥ 0 Þ x ≥ 1
x − 1 =2 + 3x
Û 3x − x = −1 − 2
Û 2x = −3
\( \Rightarrow x = - \frac{3}{2}\) (loại)
• TH2: x − 1 < 0 Þ x < 1
−x + 1 = 2 + 3x
Û 3x + x = 1 − 2
Û 4x = −1
\( \Rightarrow x = - \frac{1}{4}\) (thỏa mãn)
Vậy \(x = - \frac{1}{4}\) là nghiệm của phương trình.
Câu 26:
Thực hiện phép tính:
a) 483 + (−56) + 263 + (−64)
b) 371 + (−531) + (−271) + 731
c) 3251 − 243 − 3250
d) 279 − (145 + 279)
 Xem đáp án
Xem đáp án
a) 483 + (−56) + 263 + (−64)
= 427 + 263 + (−64)
= 690 + (−64) = 262
b) 371 + (−531) + (−271) + 731
= (371 − 271) + (731 − 531)
= 100 + 200 = 300
c) 3251 − 243 − 3250
= 3251 − 3250 − 243
= 1 – 243 = −242
d) 279 − (145 + 279)
= 279 – 421 = −142.
Câu 27:
Cho số phức z thỏa mãn |z + i + 1| = |z − 2i|. Tìm giá trị nhỏ nhất |z|.
 Xem đáp án
Xem đáp án
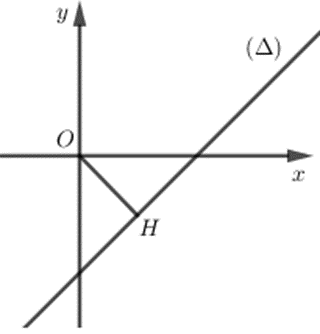
Đặt z = x + yi (x, y Î ℝ) ta được:
|(x + 1) + (y + 1)i| = |x − (y + 2)i|
Û (x + 1)2 + (y + 1)2=x2 + (y + 2)2
Û 2x + 1 + 2y + 1 = 4y + 4
Û x − y – 1 = 0.
Do đó tập hợp các số phức z thỏa mãn bài toán là đường thẳng x − y − 1 = 0.
Từ hình vẽ ta thấy |z| đạt GTNN khi
\(\left| z \right| = OH = d\left( {O,\;\left( \Delta \right)} \right) = \frac{{\left| {0 - 0 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Câu 28:
Cho số phức z thỏa mãn |z + i + 1| = |z − 2i|. Tìm giá trị nhỏ nhất |z|.
 Xem đáp án
Xem đáp án
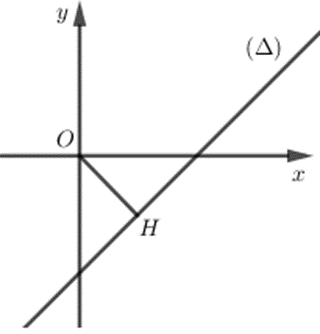
Đặt z = x + yi (x, y Î ℝ) ta được:
|(x + 1) + (y + 1)i| = |x − (y + 2)i|
Û (x + 1)2 + (y + 1)2=x2 + (y + 2)2
Û 2x + 1 + 2y + 1 = 4y + 4
Û x − y – 1 = 0.
Do đó tập hợp các số phức z thỏa mãn bài toán là đường thẳng x − y − 1 = 0.
Từ hình vẽ ta thấy |z| đạt GTNN khi
\(\left| z \right| = OH = d\left( {O,\;\left( \Delta \right)} \right) = \frac{{\left| {0 - 0 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Câu 29:
Cho số phức z thỏa mãn\(\left( {1 + 2i} \right)\left| z \right| = \frac{{\sqrt {10} }}{z} - 2 + i\). Tìm giá trị |z|.
 Xem đáp án
Xem đáp án
\(\left( {1 + 2i} \right)\left| z \right| = \frac{{\sqrt {10} }}{z} - 2 + i\)
\( \Leftrightarrow \left( {1 + 2i} \right)\left| z \right| + 2 - i = \frac{{\sqrt {10} }}{z}\)
\( \Leftrightarrow \left( {\left| z \right| + 2} \right) + \left( {2\left| z \right| - 1} \right)i = \frac{{\sqrt {10} }}{z}\)
\( \Leftrightarrow {\left( {\left| z \right| + 2} \right)^2} + {\left( {2\left| z \right| - 1} \right)^2} = \frac{{10}}{{{{\left| z \right|}^2}}}\)
\( \Leftrightarrow {\left| z \right|^2} + 4\left| z \right| + 4 + 4{\left| z \right|^2} - 4\left| z \right| + 1 = \frac{{10}}{{{{\left| z \right|}^2}}}\)
Û 5|z|4 + 5|z|2− 10 = 0
Û |z| = 1.
Câu 30:
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy C1, A1, B1 sao cho các đường thẳng AA1, BB1, CC1, đồng quy tại O. Đường thẳng qua O // AC cắt A1B1, B1C1, tại K và M tương ứng. CMR: OK = OM
 Xem đáp án
Xem đáp án
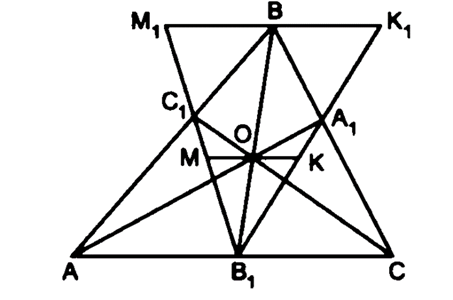
Qua B vẽ đường thẳng song song với AC cắt A1B1 và B1C1 lần lượt tại K1 và M1.
Theo giả thiết: MK // AC
Mà M1K1 // AC (theo cách vẽ)
Suy ra: MK // M1K1.
Xét tam giác B1K1M1 có MK // M1K1
Suy ra: \[\frac{{MO}}{{B{M_1}}} = \frac{{OK}}{{B{K_1}}}\] (*)
Xét tam giác AB1C1 và tam giác BM1C1 có:
\(\widehat {A{C_1}{B_1}} = \widehat {B{C_1}{M_1}}\) (2 góc đối đỉnh)
\(\widehat {A{B_1}{C_1}} = \widehat {B{M_1}{C_1}}\) (2 góc so le trong vì AC // M1K1)
Suy ra: ∆AB1C1 ᔕ ∆BM1C1 (g.g)
Nên \(\frac{{B{M_1}}}{{A{B_1}}} = \frac{{B{C_1}}}{{A{C_1}}} \Rightarrow B{M_1} = A{B_1}.\frac{{B{C_1}}}{{A{C_1}}}\;\left( 1 \right)\)
Tương tự: ∆CB1A1 ᔕ ∆BK1A1 (g.g)
Nên \(\frac{{B{K_1}}}{{C{B_1}}} = \frac{{B{A_1}}}{{C{A_1}}} \Rightarrow B{K_1} = C{B_1}.\frac{{B{A_1}}}{{C{A_1}}}\;\left( 2 \right)\)
Lấy (1) chia (2) ta được:
\(\frac{{B{M_1}}}{{B{K_1}}} = \frac{{A{B_1}}}{{B{C_1}}}\,.\,\frac{{C{A_1}}}{{B{A_1}}}\,.\,\frac{{C{B_1}}}{{A{C_1}}} = 1\)(áp dụng định lí Xê–va)
Suy ra: BM1 = BK1 (**)
Từ (*) và (**), ta có: OM = OK
Vậy OM = OK.
Câu 31:
Cho tập hợp A = {−3;−2; 0; 6; 9}.Trong các 1 tập hợp sau tập hợp nào không phải là tập hợp con của A?
 Xem đáp án
Xem đáp án
Vì −9 Ï A nên suy ra {−2; 0; −9} không phải là tập hợp con của A.
Vậy ta chọn đáp án B.
Câu 32:
Tìm ước chung của 9 và 15.
 Xem đáp án
Xem đáp án
Ta có: Ư(9) = {1; 3; 9} và Ư(15) = {1; 3; 5; 15}
Vậy ƯC(9, 15) = Ư(9) ∩ Ư(15)={1; 3}
Vậy ta chọn đáp án A.
Câu 33:
Hàm số y = cos 2x đồng biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Để hàm số y = cos 2x đồng biến thì
\(2x \in \left( {\pi + k2\pi ;\;2\pi + k2\pi } \right) \Rightarrow x \in \left( {\frac{\pi }{2} + k\pi ;\;\pi + k\pi } \right),\;k \in \mathbb{Z}\)
Vậy hàm số cos 2x đồng biến trên các khoảng \(\left( {\frac{\pi }{2} + k\pi ;\;\pi + k\pi } \right),\;k \in \mathbb{Z}\)
Câu 34:
Hàm số y = cos 2x nghịch biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Để hàm số y = cos 2x nghịch biến thì
\(2x \in \left( {k2\pi ;\;\pi + k2\pi } \right) \Rightarrow x \in \left( {k\pi ;\;\frac{\pi }{2} + k\pi } \right),\;k \in \mathbb{Z}\).
Vậy hàm số cos 2x đồng biến trên các khoảng \(\left( {\frac{\pi }{2} + k\pi ;\;\pi + k\pi } \right),\;k \in \mathbb{Z}\).
Câu 35:
Trong tam giác ABC vuông tại A có \(AC = 3a;\;AB = 3\sqrt 3 a,\;\cot B\) bằng?
 Xem đáp án
Xem đáp án
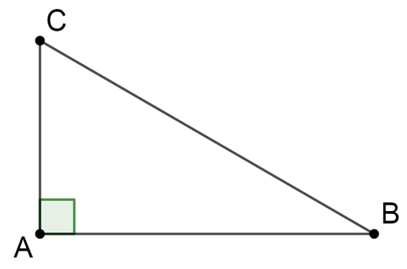
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{\left( {3\sqrt 3 a} \right)}^2} + {{\left( {3a} \right)}^2}} = 6a\).
Khi đó: \(\cot B = \frac{{AB}}{{AC}} = \frac{{3\sqrt 3 a}}{{3a}} = \sqrt 3 \).
Câu 36:
Tam giác ABC vuông tại A, AB = a, AC = 3a.Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách.
 Xem đáp án
Xem đáp án
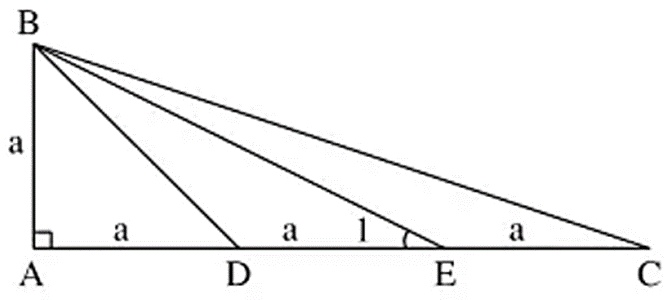
Áp dụng định lí Pytago vào tam giác ABD vuông tại A, ta có:
\(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
T a có: \(\frac{{DE}}{{DB}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\)
Mà \(\frac{{DB}}{{DC}} = \frac{{a\sqrt 2 }}{{a + a}} = \frac{{a\sqrt 2 }}{{2a}} = \frac{1}{{\sqrt 2 }}\).
Suy ra \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Xét tam giác BDE và tam giác CDB có:
\(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\)
\(\widehat {BDE}\) chung
Do đó ∆BDE ᔕ ∆CDB (c.g.c)
c) Cách 1: Xét tam giác ABD vuông tại A
Có AB = AD = a
Do đó, tam giác ABD vuông cân tại A
\[ \Rightarrow \widehat {BDA} = \widehat {ABD} = 45^\circ \]
Do ∆BDE ᔕ ∆CDB \( \Rightarrow \widehat {BED} = \widehat {CBD}\)
Mặt khác: \(\widehat {AEB} + \widehat {BCD} = \widehat {BED} + \widehat {BCD} = \widehat {CBD} + \widehat {BCD}\;\,\,\left( 3 \right)\)
Xét tam giác BCD có:
\(\widehat {ADB} = \widehat {CBD} + \widehat {BCD} = \widehat {ADB} = 45^\circ \,\,\;\left( 4 \right)\) (Tính chất góc ngoài)
Từ (3) và (4) ta suy ra \(\widehat {AEB} + \widehat {BCD} = 45^\circ \).
Cách 2: Ta có: AE = AD + DE = 2a.
Xét tam giác ABE vuông tại A
Ta có: \(\tan \widehat {AEB} = \frac{{AB}}{{AE}} = \frac{a}{{2a}} = \frac{1}{2} \Rightarrow \widehat {AEB} \approx 26^\circ 34'\).
Xét tam giác ABC vuông tại A
Ta có: \(\tan \widehat {ACB} = \frac{{AB}}{{AC}} = \frac{a}{{3a}} = \frac{1}{3} \Rightarrow \widehat {ACB} \approx 18^\circ 26'\).
Suy ra \(\widehat {AEB} + \widehat {ACB} = 26^\circ 34' + 18^\circ 26' = 45^\circ \).
Vậy \(\widehat {AEB} + \widehat {BCD} = \widehat {AEB} + \widehat {ACB} = 45^\circ \).
Câu 37:
Trên một bản đồ tỉ lệ 1 : 1 000 có hình vẽ một khu đất hình chữ nhật với chiều dài 6 cm và chiều rộng 4 cm. Tính diện tích khu đất đó bằng đơn vị ha.
 Xem đáp án
Xem đáp án
Chiều dài thật khu đất đó là:
6 × 1 000 = 6 000 (cm)
Chiều rộng thật khu đất đó là:
4 × 1 000 = 4 000 (cm)
Diện tích khu đất đó là:
6 000 × 4 000 = 24 000 000 (cm2)
Đổi: 24 000 000 cm2 = 0,24 ha
Đáp số: 0,24 ha.
Câu 38:
Hình vẽ một mảnh đất hình chữ nhật trên bản đồ tỉ lệ 1 : 1000 có chiều dài 8 cm, chiều rộng 6 cm. Vậy diện tích thực tế của mảnh đất đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Chiều dài thật mảnh đất đó là:
8 × 1 000 = 8 000 (cm)
Chiều rộng thật mảnh đất đó là:
6 × 1 000 = 6 000 (cm)
Diện tích mảnh đất đó là:
8 000 × 6 000 = 48 000 000 (cm2)
Đổi: 48 000 000 cm2 = 0,48 ha
Đáp số: 0,48 ha.
Câu 39:
Cho f(x) = −x2 − 2(m − 1)x + 2m − 1.
Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)
 Xem đáp án
Xem đáp án
f(x) = −x2 − 2(m − 1)x + 2m − 1
Xét ∆’ = (m − 1)2− (−1)(2m − 1) = m2 ≥ 0, "x Îℝ
• TH1: ∆’= 0 Þ m = 0
Khi đó f(x) = −x2 + 2x − 1 = −(x − 1)2 ≤ 0, "x Îℝ
Vậy với m = 0 không thỏa mãn yêu cầu bài toán
• TH2: ∆’ > 0 Þ m ≠ 0
Khi đó f(x) = 0 cho hai nghiệm a, b
Ta có BBT của f(x) = 0 như sau:
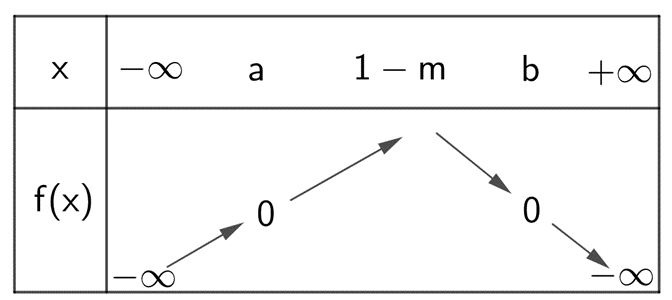
Để f(x) > 0 đúng với mọi x thuộc (0; 1) thì:
\(\left\{ \begin{array}{l}f\left( 0 \right) \le 0\\f\left( 1 \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \le 0\\0 \ge 0\end{array} \right. \Leftrightarrow m \le \frac{1}{2}\)
Vậy \(m \le \frac{1}{2}\) là giá trị thỏa mãn.
Câu 40:
Tìm m để mọi x Î [0; +∞) đều là nghiệm của bất phương trình:
(m2 − 1)x2 − 8mx + 9 − m2 ≥ 0
Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)
 Xem đáp án
Xem đáp án
(m2 − 1)x2 − 8mx + 9 − m2 ≥ 0 (1)
+) \({m^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\)
• Với m = 1, bất phương trình có dạng −8x + 8 ≥ 0 Û x ≤ 1.
Do đó m = 1 không thỏa mãn.
• Với m = −1, bất phương trình có dạng 8x + 8 ≥ 0 Û x ≥ −1.
Do đó m = −1 là một giá trị cần tìm.
+) m2 − 1 ≠ 0 Û m ≠ ±1
Khi đó vế trái là tam thức bậc hai có ’= m4+6m2+ 9 > 0, "mÎℝ
Vaạy nên tam thức luôn có hai nghiệm a < b
Suy ra mọi x Î [0; +∞) đều là nghiệm của bất phương trình:
(m2 − 1)x2 − 8mx + 9 − m2 ≥ 0 khi và chỉ khi:
\(\left\{ \begin{array}{l}{m^2} - 1 > 0\\{x_1} < {x_2} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 1 > 0\\{x_1} + {x_2} = \frac{{8m}}{{{m^2} - 1}} < 0\\{x_1}{x_2} = \frac{{9 - {m^2}}}{{{m^2} - 1}} \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m - 1\end{array} \right.\\\left[ \begin{array}{l}0 < m < 1\\m < - 1\end{array} \right.\\\left[ \begin{array}{l} - 3 \le m < - 1\\1 < m \le 3\end{array} \right.\end{array} \right. \Leftrightarrow - 3 \le m < - 1\)
Từ đó suy ra m Î [−3; −1].
Câu 41:
Tìm ba số, biết tổng thứ nhất và thứ hai bằng 182. Tổng của số thứ hai và thứ ba bằng 176, tổng của số thứ ba và số thứ nhất bằng 188.
 Xem đáp án
Xem đáp án
Tổng 3 số là:
(182+176+188): 2 = 273
Số thứ nhất là:
273 − 176 = 97
Số thứ 2 là:
182 − 97 = 85
Số thứ 3 là:
176 − 85 = 91
Đáp số: 97, 85 và 91.
Câu 42:
Tổng của số thứ nhất và số thứ hai là 18,36;tổng của số thứ hai và số thứ ba là 21,64; tổng của số thứ ba và số thứ nhất là 20. Tính tổng của ba số đó?
 Xem đáp án
Xem đáp án
Tổng của 3 số là:
(18,36 + 21,64 + 20) : 2 = 30
Đáp số: 30.
Câu 43:
Tam giác ABC có AB = 2, AC = 1 và \(\widehat A = 60^\circ .\) Tính độ dài cạnh BC.
 Xem đáp án
Xem đáp án
Theo định lí hàm cosin, ta có:
\[B{C^2} = A{B^2} + A{C^2} - 2AB\,.\,AC\,.\,\cos \widehat A\]
= 22 + 12 − 2.2.1.cos 60°= 3
\[ \Rightarrow BC = \sqrt 3 \].
Câu 44:
Cho tam giác ABC, \(AB = a,\;AC = a\sqrt 3 ,\;\widehat {BAC} = 60^\circ \) và \(\widehat A = 60^\circ .\) Tính diện tích tam giác ABC theo a.
 Xem đáp án
Xem đáp án
Ta có: \({S_{ABC}} = \frac{1}{2}AB\,.\,AC\,.\,\sin \widehat {BAC} = \frac{1}{2}\,.\,a\,.\,a\sqrt 3 \,.\,\sin 60^\circ = \frac{{3{a^2}}}{4}\).
Câu 45:
Cho hình chóp S.ABCD có AD và BC không song song.Gọi M,N lần lượt là trung điểm của SB và SC.Tìm giao tuyến của (SAD) và (SBC).Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (AMN).
 Xem đáp án
Xem đáp án
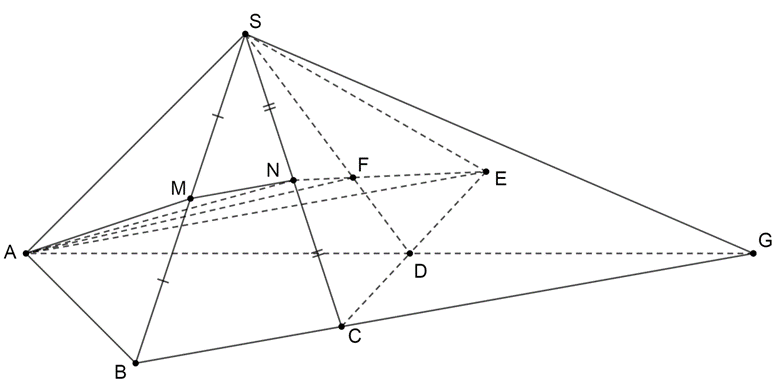
Kéo dài AD và BC cắt nhau tại G
G Î BC Ì (SBC)
G Î AD Ì (SAD)
Þ G Î (SBC) Ç (SAD)
Lại có: S Î (SBC) Ç (SAD)
Nên suy ra SG = (SBC) Ç (SAD)
Qua A kẻ đường thẳng song song với BC cắt CD tại E
Khi đó với M, N lần lượt là trung điểm của SB và SC nên MN là đường trung bình của tam giác SBC
Suy ra MN // BC
Do đó với AE // BC thì MN // AE
Suy ra A, M, N, E đồng phẳng
Lấy F là giao điểm của NE và SD
Do F Î NE Ì (AMNE) Þ F Î (AMN)
Mà F Î SD Þ F = (AMN) Ç SD
Theo cách dựng bên trên, tứ giác AMNF chính là thiết diện của (AMN) và hình chóp.
Câu 46:
Cho hình chóp S.ABCD có AD và BC không song song. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của (SAD) và (SBC).
b) Chứng minh MN // (ABCD).
c) Tìm giao điểm của đường thẳng SD với (AMN).
 Xem đáp án
Xem đáp án
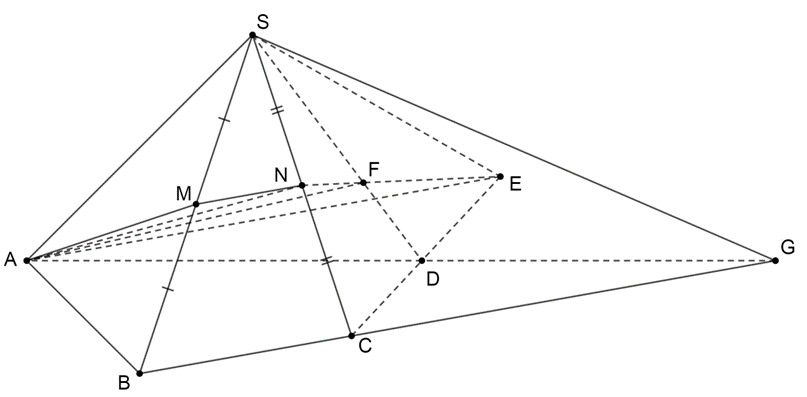
a) Kéo dài AD và BC cắt nhau tại G
• G Î BC Ì (SBC)
• G Î AD Ì (SAD)
Do đó G Î (SBC) Ç (SAD)
Lại có: S Î (SBC) Ç (SAD)
Nên suy ra SG = (SBC) Ç (SAD)
b) Với M, N lần lượt là trung điểm của SB và SC nên MN là đường trung bình của tam giác SBC
Suy ra MN // BC
Mà BC Ì (ABCD)
Do đó MN // (ABCD).
c) Qua A kẻ đường thẳng song song với BC cắt CD tại E
Do đó với AE // BC thì MN // AE
Suy ra A, M, N, E đồng phẳng.
Lấy F là giao điểm của NE và SD
Do F Î NE Ì (AMNE) Þ F Î (AMN)
Mà F Î SD Þ F = (AMN) Ç SD.
Câu 47:
Cho hình chóp S.ABC, đáy ABC là tamgiác đều cạnh a; SA ^ (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của Alên SB; SC. Tính diện tích mặt cầu đi qua 5 điểm A, B, C, K, H.
 Xem đáp án
Xem đáp án
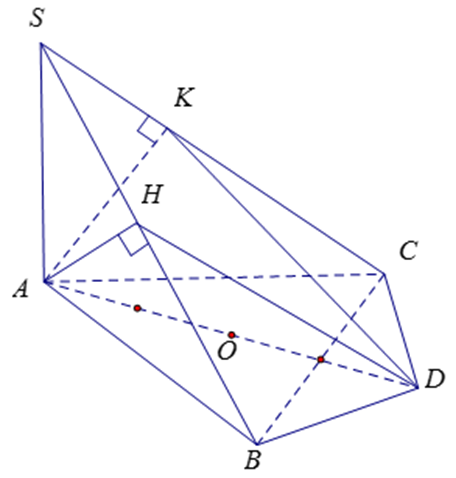
Gọi AD là đường kính đường tròn ngoại tiếp ∆ABC (1)
Ta có: \(\left\{ \begin{array}{l}AH \bot SB\;\left( {gt} \right)\\AH \bot DB\end{array} \right. \Rightarrow AH \bot \left( {SBD} \right)\)
Suy ra AH ^ HD (2)
Chứng minh tương tự ta được: AK ^ KD (3)
Từ (1), (2), (3) ta suy ra 5 điểm A B, C, H, K cùng nằm trên mặt cầu đường kính AD.
Gọi O là trung điểm của AD, ta có:
\(R = AO = \frac{{a\sqrt 3 }}{3}\) (vì ∆ABC là tam giác đều có cạnh là a0
Vậy diện tích mặt cầu đi qua 5 điểm A, B, C, H, K là:
\(S = 4\pi {R^2} = 4\pi {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = \frac{{4\pi {a^2}}}{3}.\)
Câu 48:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng đáy.
 Xem đáp án
Xem đáp án
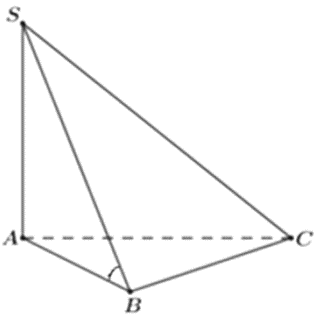
SA vuông góc với mặt phẳng (ABC) nên góc giữa SB và mặt phẳng (ABC) là \[\widehat {SBA}\].
Xét tam giác SBA vuông tại A ta có:
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {SBA} = 45^\circ \).
Câu 49:
Cho a ≥ 1; b ≥ 9; c ≥ 16 thỏa mãn a.b.c = 1 152. Tìm giá trị lớn nhất của biểu thức: \(P = bc\sqrt {a - 1} + ca\sqrt {b - 9} + ab\sqrt {c - 16} \).
 Xem đáp án
Xem đáp án
\(P = bc\sqrt {a - 1} + ca\sqrt {b - 9} + ab\sqrt {c - 16} \)
\( \Leftrightarrow \frac{P}{{abc}} = \frac{{\sqrt {a - 1} }}{a} + \frac{{\sqrt {b - 9} }}{b} + \frac{{\sqrt {c - 16} }}{c}\)
\( \Leftrightarrow \frac{P}{{1152}} = \frac{{\sqrt {a - 1} }}{a} + \frac{{\sqrt {b - 9} }}{b} + \frac{{\sqrt {c - 16} }}{c}\)
Áp dụng BĐT AM - GM:
\(\left\{ \begin{array}{l}2\sqrt {a - 1} \le a - 1 + 1 = a\\2\sqrt {9\left( {b - 9} \right)} \le b - 9 + 9 = b\\2\sqrt {16\left( {c - 16} \right)} \le c - 16 + 16 = c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{\sqrt {a - 1} }}{a} \le \frac{1}{2}\\\frac{{\sqrt {b - 9} }}{b} \le \frac{1}{6}\\\frac{{\sqrt {c - 16} }}{c} \le \frac{1}{8}\end{array} \right.\)
Khi đó \(\frac{P}{{1152}} = \frac{{\sqrt {a - 1} }}{a} + \frac{{\sqrt {b - 9} }}{b} + \frac{{\sqrt {c - 16} }}{c} \le \frac{1}{2} + \frac{1}{6} + \frac{1}{8} = \frac{{19}}{{24}}\)
Û P ≤ 912
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b - 9 = 9\\c - 16 = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 18\\c = 32\end{array} \right.\)
Vậy GTLN của P là 912 khi (a; b; c) = (1; 18; 32).
Câu 50:
Cho B=3 + 32 + 33 + ... + 3120. Chứng minh:
a) B chia hết cho 3;
b) B chia hết cho 4;
c) B chia hết cho 13.
 Xem đáp án
Xem đáp án
a) B = 3 + 32 + 33 + ... + 3120
= 3(1 + 3 + 32 + ... + 3119)
Vì 3 ⋮ 3 Þ3(1 + 3 + 32 + ... + 3119) ⋮ 3
Vậy suy ra B ⋮ 3
b) B = 3 + 32 + 33 + ... + 3120
= (3 + 32) + (33 + 34) +... + (3119 + 3120)
= 3(1 + 3) + 33(1 + 3) +... + 3119(1 + 3)
= 3.4 + 33.4 + ... + 3119.4
= 4(3 + 33 + ... + 3119)
Vì 4 ⋮ 4 Þ 4(3 + 33 + ... + 3119) ⋮ 4
Vậy suy ra B ⋮ 4
c) B = 3 + 32 + 33 + ... + 3120
= (3 + 32 + 33) + (34 + 35 + 36) +... + (3118 + 3119 + 3120)
= 3(1 + 3 + 32) + 34(1 + 3 + 32) + ... + 3118(1 + 3 + 32)
= 3.13 + ... + 3118.13
= 13(3 + 34 + ... + 3118)
Vì 13 ⋮ 13 nên 13(3 + 34 + ... + 3118) ⋮ 13
Vậy suy ra B ⋮ 13
Câu 51:
Cho B = 3 + 32 + 33 + ... + 3120. Chứng minh B chia hết cho 13.
 Xem đáp án
Xem đáp án
B = 3 + 32 + 33 + ... + 3120
= (3 + 32 + 33) + (34 + 35 + 36) +... + (3118 + 3119 + 3120)
= 3(1 + 3 + 32) + 34(1 + 3 + 32) + ... + 3118(1 + 3 + 32)
= 3.13 + ... + 3118.13
= 13(3 + 34 + ... + 3118)
Vì 13 ⋮ 13 nên 13(3 + 34 + ... + 3118) ⋮ 13
Vậy suy ra B ⋮ 13
Câu 52:
Chứng minh rằng biểu thức:
a) x2 + 2x + 3 luôn dương với mọi x;
b) −x2 + 4x − 5 luôn âm với mọi x.
 Xem đáp án
Xem đáp án
a) Ta có: x2 + 2x + 3 = (x2 + 2x + 1) + 2
= (x + 1)2 + 2
Vì (x + 1)2 ≥ 0, " x Îℝ
Suy ra (x + 1)2 + 2 ≥ 2, " x Îℝ
Vậy x2 + 2x + 3 luôn dương với mọi x
b) Ta có: −x2 + 4x − 5 = −(x2 − 4x + 4) − 1
= −(x − 2)2 − 1
Vì (x − 2)2 ≥ 0, " x Îℝ
Suy ra −(x − 2)2 ≤ 0, " x Îℝ
Þ−(x − 2)2 − 1 ≤ −1, " x Îℝ
Vậy −x2 + 4x − 5 luôn âm với mọi x.
Câu 53:
Chứng minh 4x − 10 − x2 luôn luôn âm với mọi x.
 Xem đáp án
Xem đáp án
Ta có: 4x − 10 − x2= −(x2 − 4x + 4) − 6
= −(x − 2)2 − 6
Vì (x − 2)2 ≥ 0, " x Îℝ
Suy ra −(x − 2)2 ≤ 0, " x Îℝ
Þ−(x − 2)2 − 6 ≤ −6, " x Îℝ
Vậy 4x − 10 − x2 luôn luôn âm với mọi x.
Câu 54:
Giải phương trình: \(\frac{{{{\cot }^2}x - {{\tan }^2}x}}{{\cos 2x}} = 16\left( {1 + \cos 4x} \right)\).
 Xem đáp án
Xem đáp án
Ta có: \({\cot ^2}x - {\tan ^2}x = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}} - \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\)
\( = \frac{{{{\cos }^4}x - {{\sin }^4}x}}{{{{\sin }^2}x\,.\,{{\cos }^2}x}} = \frac{{4\cos 2x}}{{{{\sin }^2}2x}}\).
Điều kiện: \(\left\{ \begin{array}{l}\sin 2x \ne 0\\\cos 2x \ne 0\end{array} \right. \Leftrightarrow \sin 4x \ne 0\)
Lúc đó: \(\frac{{{{\cot }^2}x - {{\tan }^2}x}}{{\cos 2x}} = 16\left( {1 + \cos 4x} \right)\)
\[ \Leftrightarrow \frac{4}{{{{\sin }^2}2x}} = 16\left( {1 + \cos 4x} \right)\]
Û 1 = 4(1 + cos 4x)sin2 2x
Û 1 = 2(1 + cos 4x)(1 − cos 4x)
Û 1 = 2(1 – cos2 4x)
Û 1 = 2sin2 4x
Û 1 = 1 – cos 8x
Ûcos 8x = 0
\( \Leftrightarrow x = \frac{\pi }{{16}} + \frac{{k\pi }}{8},\;k \in \mathbb{Z}\) (thỏa mãn)
Vậy họ nghiệm của phương trình là: \(x = \frac{\pi }{{16}} + \frac{{k\pi }}{8},\;k \in \mathbb{Z}\).
Câu 55:
Giải phương trình: cot2 x – tan2 x = 16cos 2x.
 Xem đáp án
Xem đáp án
Ta có: \({\cot ^2}x - {\tan ^2}x = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}} - \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\)
\( = \frac{{{{\cos }^4}x - {{\sin }^4}x}}{{{{\sin }^2}x\,.\,{{\cos }^2}x}} = \frac{{4\cos 2x}}{{{{\sin }^2}2x}}\).
Điều kiện: \(\left\{ \begin{array}{l}\sin 2x \ne 0\\\cos 2x \ne 0\end{array} \right. \Leftrightarrow \sin 4x \ne 0\).
Lúc đó: cot2 x – tan2 x = 16cos 2x
\( \Leftrightarrow \frac{{4\cos 2x}}{{{{\sin }^2}2x}} = 16\cos 2x\)
\( \Leftrightarrow \cos 2x\left( {\frac{1}{{{{\sin }^2}2x}} - 4} \right) = 0\)
+) TH1: cos 2x = 0
\( \Rightarrow 2x = \frac{\pi }{2} + k\pi ,\;k \in \mathbb{Z}\)
\( \Rightarrow x = \frac{\pi }{4} + k\frac{\pi }{2},\;k \in \mathbb{Z}\) (thỏa mãn)
+) TH2: \(\frac{1}{{{{\sin }^2}2x}} - 4 = 0\)
\( \Leftrightarrow {\sin ^2}2x = \frac{1}{4}\)
\( \Leftrightarrow \sin 2x = \pm \frac{1}{2}\)
• Với \(\sin 2x = \frac{1}{2}\), ta có:
\(\left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \;\left( {k \in \mathbb{Z}} \right)\\2x = \frac{{5\pi }}{6} + k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \;\left( {k \in \mathbb{Z}} \right)\\x = \frac{{5\pi }}{{12}} + k\pi \;\left( {k \in \mathbb{Z}} \right)\end{array} \right.\) (thỏa mãn)
- Với \(\sin 2x = - \frac{1}{2}\), ta có:
\(\left[ \begin{array}{l}2x = - \frac{\pi }{6} + k2\pi \;\left( {k \in \mathbb{Z}} \right)\\2x = \frac{{7\pi }}{6} + k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} + k\pi \;\left( {k \in \mathbb{Z}} \right)\\x = \frac{{7\pi }}{{12}} + k\pi \;\left( {k \in \mathbb{Z}} \right)\end{array} \right.\) (thỏa mãn)
Vậy các họ nghiệm của phương trình là:
\(x \in \left\{ {\frac{\pi }{4} + k\frac{\pi }{2};\; \pm \frac{\pi }{{12}} + k\pi ;\;\frac{{5\pi }}{{12}} + k\pi ;\;\frac{{7\pi }}{{12}} + k\pi \;\left( {k \in \mathbb{Z}} \right)} \right\}\)
Câu 56:
Cho 2 số x, y > 0 thỏa mãn x + y = 1.
Tìm GTNN của: \(P = {\left( {2x + \frac{1}{x}} \right)^2} + {\left( {2y + \frac{1}{y}} \right)^2}\).
 Xem đáp án
Xem đáp án
Áp dụng BĐT AM – GM ta có:
\(P = {\left( {2x + \frac{1}{x}} \right)^2} + {\left( {2y + \frac{1}{y}} \right)^2} \ge \frac{{{{\left( {2x + \frac{1}{x} + 2y + \frac{1}{y}} \right)}^2}}}{2}\)
\( = \frac{{{{\left[ {2\left( {x + y} \right) + \left( {\frac{1}{x} + \frac{1}{y}} \right)} \right]}^2}}}{2} \ge \frac{{{{\left( {2 + \frac{4}{{x + y}}} \right)}^2}}}{2} = \frac{{{{\left( {2 + 4} \right)}^2}}}{2} = 18\)
Dấu “=” xảy ra khi và chỉ khi \(x = y = \frac{1}{2}\).
Vậy GTNN của P = 18 khi \(x = y = \frac{1}{2}\).
Câu 57:
Cho 2 số dương x, y thay đổi thỏa mãn xy = 2. Tìm GTNN của biểu thức:\(M = \frac{1}{x} + \frac{2}{y} + \frac{3}{{2x + y}}\).
 Xem đáp án
Xem đáp án
Ta có: \(M = \frac{1}{x} + \frac{2}{y} + \frac{3}{{2x + y}} = \frac{{2x + y}}{{xy}} + \frac{3}{{2x + y}}\)
\( = \frac{{2x + y}}{2} + \frac{3}{{2x + y}} = \left( {\frac{3}{8}\,.\,\frac{{2x + y}}{2} + \frac{3}{{2x + y}}} \right) + \frac{5}{8}\,.\,\frac{{2x + y}}{2}\)
Áp dụng BĐT AM – GM ta có:
\(\frac{3}{8}\,.\,\frac{{2x + y}}{2} + \frac{3}{{2x + y}} \ge 2\sqrt {\frac{3}{8}\,.\,\frac{{2x + y}}{2}\,.\frac{3}{{2x + y}}} = \frac{3}{2}\)
Dấu “=” xảy ra khi và chỉ khi: \(\frac{3}{8}\,.\,\frac{{2x + y}}{2} = \frac{3}{{2x + y}} \Rightarrow 2x + y = 4\) (do x; y > 0)
Lại có: \(\frac{5}{8}\,.\,\frac{{2x + y}}{2} \ge \frac{5}{8}\sqrt {2xy} = \frac{5}{4}\)
Dấu “=” xảy ra khi và chỉ khi: 2x = y và xy = 2
Do đó: \(M \ge \frac{3}{2} + \frac{5}{4} = \frac{{11}}{4}\)
Dấu “=” xảy ra khi và chỉ khi: x = 1; y = 2
Vậy GTNN của M là \(\frac{{11}}{4}\) khi x = 1; y = 2.
Câu 58:
Tìm GTNN của B = 2x2+3y2+4xy − 8x − 2y + 18
 Xem đáp án
Xem đáp án
B = 2x2 + 3y2 + 4xy − 8x − 2y + 18
Þ 2B = 4x2 + 6y2 + 8xy − 16x − 4y + 36
= (4x2 + 8xy + 4y2) + 2y2 − 16x − 4y + 36
= [(2x + 2y)2 − 2(2x + 2y).4 + 16] + (2y2 + 12y + 18) + 2
= (2x + 2y − 2)2 + 2(y2 + 6y + 9) + 2
= (2x + 2y − 2)2 + 2(y + 3)2 + 2 ≥ 2
Dấu “=” xảy ra khi và chỉ khi: \[\left\{ \begin{array}{l}2x + 2y - 2 = 0\\y + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = - 3\end{array} \right.\]
Vậy GTNN của B là 2 khi x = 4; y =−3.
Câu 59:
Cho tam giác ABC có M là điểm chính giữa cạnh AB. Trên cạnh AC lấy điểm N sao cho CN = 2AN.Đoạn thẳng BN cắt CM ở O.Biết diện tích tam giác OBC bằng 20cm2. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
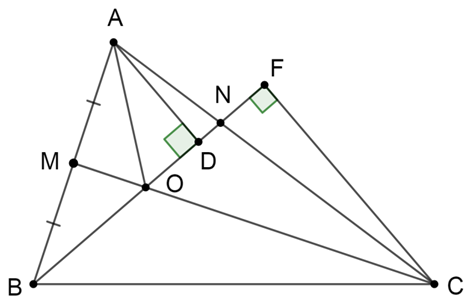
Kẻ hai đường cao AD, CF tới đường thẳng BN.
Ta có: M là điểm chính giữa cạnh AB\( \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\)
CN = 2AN\( \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3}\)
SAOM = SBOM (Do có cùng chiều cao hạ từ O xuống AB và đáy MA = MB)
Mà SACM = SBCM (Do có cùng chiều cao hạ từ C xuống AB và đáy MA = MB)
Nên suy ra SAOC = SBOC
Lại có: \({S_{AON}} = \frac{1}{2}{S_{CON}}\) (Do có cùng chiều cao hạ từ O xuống AC và đáy CN = 2AN)
Do đó nếu coi A, C là đỉnh thì 2 tam giác trên có diện tích gấp đôi nhưng chung đáy ON nên chiều cao phải gấp đôi nhau
Suy ra \(AD = \frac{1}{2}CF\)
Do đó \({S_{AOB}} = \frac{1}{2}{S_{COB}}\) (do có chung đáy OB mà hai đường cao\(AD = \frac{1}{2}CF\))
Vậy \({S_{ABC}} = {S_{AOB}} + {S_{OBC}} + {S_{AOC}} = \frac{1}{2}{S_{OBC}} + {S_{OBC}} + {S_{OBC}} = \frac{5}{2}\,.\,20 = 50\;\left( {c{m^2}} \right)\)
Câu 60:
Cho tam giác ABC. Điểm M là điểm chính giữa cạnh AB. Trên cạnh AC lấy AN bằng \(\frac{1}{2}\) NC. Hai đoạn thẳng BN và CM cắt nhau tại K. Hãy tính diện tích tam giác AKC? Biết diện tích tam giác KAB bằng 42 dm2.
 Xem đáp án
Xem đáp án
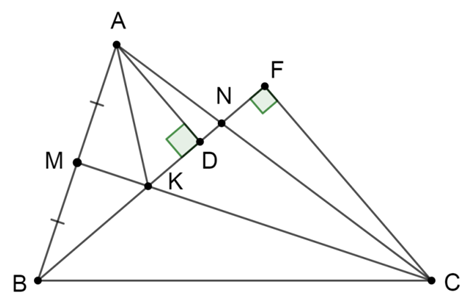
Kẻ hai đường cao AD, CF tới đường thẳng BN.
Ta có: M là điểm chính giữa cạnh AB\( \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\)
CN = 2AN\( \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3}\)
SAKM = SBKM (Do có cùng chiều cao hạ từ K xuống AB và đáy MA = MB)
Mà SACM = SBCM (Do có cùng chiều cao hạ từ C xuống AB và đáy MA = MB)
Nên suy ra SAKC = SBKC
Lại có: \({S_{AKN}} = \frac{1}{2}{S_{CKN}}\) (Do có cùng chiều cao hạ từ K xuống AC và đáy CN = 2AN)
Do đó nếu coi A, C là đỉnh thì 2 tam giác trên có diện tích gấp đôi nhưng chung đáy NK nên chiều cao phải gấp đôi nhau
Suy ra \(AD = \frac{1}{2}CF\)
Do đó \({S_{AOB}} = \frac{1}{2}{S_{COB}}\) (Do có chung đáy OB mà hai đường cao\(AD = \frac{1}{2}CF\))
Vậy \({S_{AKC}} = {S_{BKC}} = 2{S_{KAB}} = 2\,.\,42 = 84\;\left( {d{m^2}} \right)\)
Câu 61:
Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(−4; 1), B(2; 4), C(2; −2).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Tìm tọa độ điểm D sao cho C là trọng tâm của tam giác ABD.
c) Tìm tọa độ điểm E sao cho tứ giác ABCE là hình bình hành.
 Xem đáp án
Xem đáp án
a) Gọi G là trọng tâm của tam giác ABC có tọa độ G(xG; yG).
Ta có: \(\left\{ \begin{array}{l}{x_G} = \frac{{ - 4 + 2 + 2}}{3} = 0\\{y_G} = \frac{{1 + 4 - 2}}{3} = 1\end{array} \right.\).
Vậy tọa độ trọng tâm G của tam giác ABC là G(0; 1).
b) Gỉả sử điểm D có tọa độ là D(xD; yD)
Vì C là trọng tâm của tam giác ABD nên ta có:
\(\left\{ \begin{array}{l}\frac{{ - 4 + 2 + {x_D}}}{3} = 2\\\frac{{1 + 4 + {y_D}}}{3} = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 + 2 + {x_D} = 6\\1 + 4 + {y_D} = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = - 11\end{array} \right.\)
Vậy điểm D có tọa độ là D(8; −11).
c) Gỉả sử điểm D có tọa độ là E(xE; yE).
Để tứ giác ABCE là hình bình hành thì \(\overrightarrow {AB} = \overrightarrow {EC} \)
\[ \Leftrightarrow \left( {2 + 4;\;4 - 1} \right) = \left( {2 - {x_E};\; - 2 - {y_E}} \right)\]
\( \Leftrightarrow \left\{ \begin{array}{l}2 - {x_E} = 6\\ - 2 - {y_E} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 4\\{y_E} = - 5\end{array} \right.\)
Vậy điểm E có tọa độ là E(−4; −5).
Câu 62:
Trong mặt phẳng tọa độ Oxy, cho A(−4; 1), B(2; 4), C(2; −2). Chứng minh rằng 3 điểm A B, C tạo thành tam giác.
 Xem đáp án
Xem đáp án
Để 3 điểm A B, C tạo thành tam giác thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) phải không cùng phương.
Ta có: \(\overrightarrow {AB} = \left( {2 + 4;\;4 - 1} \right) = \left( {6;\;3} \right)\)
\(\overrightarrow {AC} = \left( {2 + 4;\; - 2 - 1} \right) = \left( {6;\; - 3} \right)\)
\( \Rightarrow \frac{6}{6} \ne \frac{3}{{ - 3}}\;\left( {1 \ne - 1} \right)\).
Vậy 3 điểm A B, C tạo thành tam giác.
Câu 63:
Cho x, y, z là các số thực không âm thỏa mãn x+y+ z = 1. Tìm GTLN của biểu thức:\(P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1} \).
 Xem đáp án
Xem đáp án
Do x; y; z ≥ 0 và x+y+ z = 1 nên suy ra 0 ≤ x; y; z ≤ 1
\( \Rightarrow \left\{ \begin{array}{l}{x^2} \le x\\{y^2} \le y\\{z^2} \le z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2{x^2} + x + 1 \le {x^2} + 2x + 1\\2{y^2} + y + 1 \le {y^2} + 2y + 1\\2{z^2} + z + 1 \le {z^2} + 2z + 1\end{array} \right.\)
\( \Rightarrow P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1} \)
\( \le \sqrt {{{\left( {x + 1} \right)}^2}} + \sqrt {{{\left( {y + 1} \right)}^2}} + \sqrt {{{\left( {z + 1} \right)}^2}} \)
= x + y + z + 3 = 4
Vậy Pmax = 4 khi (x; y; z) = (0; 0; 1) và các hoán vị.
Câu 64:
Cho x2 + y2 + xy = 1. Tìm GTNN, GTLN của: A = x2 − xy + 2y2
 Xem đáp án
Xem đáp án
Vì x2 + y2 + xy = 1 nên \(A = \frac{{{x^2} - xy + 2{y^2}}}{{{x^2} + {y^2} + xy}}\)
• Với y = 0 Þ A = 1
• Với y ≠ 0 ta chia cả tử và mẫu của vế phải cho y2
Suy ra \[A = \frac{{{{\left( {\frac{x}{y}} \right)}^2} - \frac{x}{y} + 2}}{{{{\left( {\frac{x}{y}} \right)}^2} + \frac{x}{y} + 1}}\]
Đặt \(\frac{x}{y} = a \Rightarrow A = \frac{{{a^2} - a + 2}}{{{a^2} + a + 1}}\)
Û A.a2 + A.a + A = a2 − a + 2
Û (A − 1).a2 + (A + 1).a + A − 2 = 0
Ta có: ∆ = (A + 1)2− 4(A − 1)(A − 2) ≥0
Û −3A2 + 14A − 7 ≥ 0
\( \Rightarrow \frac{{7 - 2\sqrt 7 }}{3} \le A \le \frac{{7 + 2\sqrt 7 }}{3}\)
Vậy \(\left\{ \begin{array}{l}{A_{\max }} = \frac{{7 + 2\sqrt 7 }}{3}\\{A_{\min }} = \frac{{7 - 2\sqrt 7 }}{3}\end{array} \right.\).
Câu 65:
Cho (O) và (O') cắt nhau tại A và B. Vẽ hình bình hành OBO'C.
Chứngminh: AC//OO'
 Xem đáp án
Xem đáp án
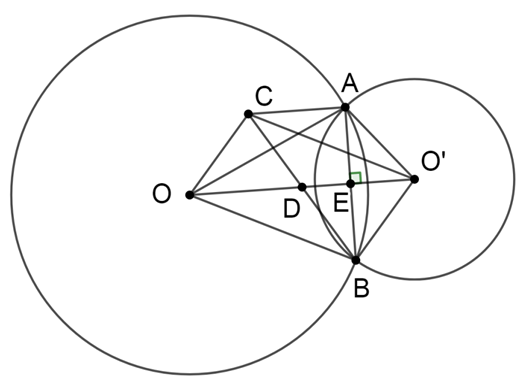
Lấy E = AB Ç OO’ và D = BC Ç OO’
Do hai đường tròn (O) và (O') cắt nhau tại A và B nên OA = OB và O’A = O’B
Suy ra OO’ là đường trung trực của đoạn thẳng AB
Do đó AB ^ OO’
Và D nằm trên đường trung trực OO’ nên suy ra DA = DB
Do D là giao điểm của hai đường chéo của hình bình hành OBO’C nên suy ra D là trung điểm của BC
\( \Rightarrow CD = BD = DA = \frac{{BC}}{2}\)
∆ABC có AD là trung tuyến và \(DA = \frac{{BC}}{2}\)
Þ ∆ABC vuông tại A
Þ AB ^ AC mà OO’ ^ AB
Vậy AC // OO’.
Câu 66:
Cho hai đường tròn (O) và (O¢) cắt nhau tại A và B như hình bên. Biết OA =15cm, O¢A = 13cm, AB = 24cm. Tính độ dài OO¢.
 Xem đáp án
Xem đáp án
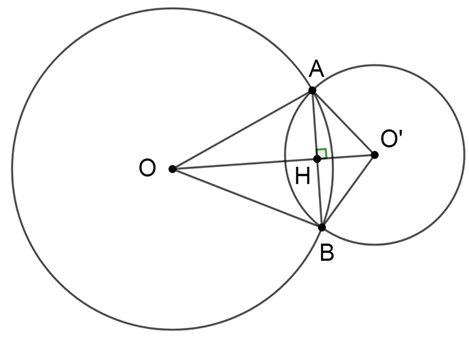
Gọi H là giao điểm của AB và OO¢.
Vì OO¢ là đường trung trực của AB nên:
OO¢ ^ AB tại H
Suy ra: \(HA = HB = \frac{1}{2}AB = \frac{1}{2}\,.\,24 = 12\;\left( {cm} \right)\)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
AO2 = OH2 + AH2
Suy ra: OH2 = AO2 − AH2 = 152 − 122 = 81
Þ OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO¢H, ta có:
AO¢2 = O¢H2 + AH2
Suy ra: O¢H2 = AO¢2 − AH2 = 132 − 122 = 25
Þ O’H = 5 (cm)
Vậy OO¢ = OH + O¢H = 9 + 5 = 14 (cm)
Câu 67:
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI và J là điểm trên BC kéo dài sao cho 5JB = 2JC. Gọi G là trọng tâm tam giác.
a) Biểu diễn \[\overrightarrow {AB} ,\;\overrightarrow {AC} \]theo hai vectơ \[\overrightarrow {AI} ,\;\overrightarrow {AJ} \]và biểu diễn \[\overrightarrow {AJ} \]qua \[\overrightarrow {AB} ,\;\overrightarrow {AC} \].
b) Biểu diễn \[\overrightarrow {AG} \]theo hai vectơ\[\overrightarrow {AI} ,\;\overrightarrow {AJ} \].
 Xem đáp án
Xem đáp án
a) I là điểm trên cạnh BC mà: \[2CI = 3BI \Rightarrow \frac{{BI}}{{CI}} = \frac{2}{3}\]
\( \Rightarrow \frac{{BI}}{{CI + BI}} = \frac{2}{{3 + 2}} \Rightarrow \frac{{BI}}{{BC}} = \frac{2}{5}\)
\( \Rightarrow BI = \frac{2}{5}BC\)
Tương tự ta có: \( \Rightarrow IC = \frac{3}{5}BC\)
J là điểm trên BC kéo dài: \[5JB = 2JC \Rightarrow \frac{{JB}}{{JC}} = \frac{2}{5}\]
\( \Rightarrow \frac{{JB}}{{JC - JB}} = \frac{2}{{5 - 2}} \Rightarrow \frac{{JB}}{{BC}} = \frac{2}{3}\)
\( \Rightarrow JB = \frac{2}{3}BC\)và\(BC = \frac{3}{5}JC\)
Ta có: \(\overrightarrow {AB} = \overrightarrow {AI} + \overrightarrow {IB} = \overrightarrow {AI} - \frac{2}{5}\overrightarrow {BC} = \overrightarrow {AI} - \frac{2}{5}\,.\,\frac{3}{2}\overrightarrow {JB} \)
\( = \overrightarrow {AI} - \,\frac{3}{5}\overrightarrow {JB} = \overrightarrow {AI} - \,\frac{3}{5}\left( {\overrightarrow {JA} + \overrightarrow {AB} } \right) = \overrightarrow {AI} + \,\frac{3}{5}\overrightarrow {AJ} - \,\frac{3}{5}\overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {AB} + \frac{3}{5}\overrightarrow {AB} = \overrightarrow {AI} + \,\frac{3}{5}\overrightarrow {AJ} \)
\( \Rightarrow \overrightarrow {AB} = \frac{5}{8}\overrightarrow {AI} + \,\frac{3}{8}\overrightarrow {AJ} \) (1)
Lại có: \(\overrightarrow {AC} = \overrightarrow {AI} + \overrightarrow {IC} = \overrightarrow {AI} + \frac{3}{5}\overrightarrow {BC} = \overrightarrow {AI} + \frac{3}{5}\,.\,\frac{3}{2}\overrightarrow {JC} \)
\( = \overrightarrow {AI} + \,\frac{9}{{25}}\overrightarrow {JC} = \overrightarrow {AI} + \,\frac{9}{{25}}\left( {\overrightarrow {JA} + \overrightarrow {AB} } \right) = \overrightarrow {AI} - \frac{9}{{25}}\overrightarrow {AJ} + \frac{9}{{25}}\overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {AC} - \frac{9}{{25}}\overrightarrow {AC} = \overrightarrow {AI} - \,\frac{9}{{25}}\overrightarrow {AJ} \)
\( \Rightarrow \overrightarrow {AC} = \frac{{25}}{{16}}\overrightarrow {AI} - \,\frac{9}{{16}}\overrightarrow {AJ} \) (2)
Nhân 2 vế của (1) với \(\frac{5}{2}\) rồi trừ cho vế với vế của (2) ta được:
\(\frac{5}{2}\overrightarrow {AB} - \overrightarrow {AC} = \frac{5}{2}\left( {\frac{5}{8}\overrightarrow {AI} + \,\frac{3}{8}\overrightarrow {AJ} } \right) - \left( {\frac{{25}}{{16}}\overrightarrow {AI} - \,\frac{9}{{16}}\overrightarrow {AJ} } \right)\)
\( = \frac{{25}}{{16}}\overrightarrow {AI} + \frac{{15}}{{16}}\overrightarrow {AJ} - \frac{{25}}{{16}}\overrightarrow {AI} + \frac{9}{{16}}\overrightarrow {AJ} = \frac{3}{2}\overrightarrow {AJ} \)
\( \Rightarrow \overrightarrow {AJ} = \frac{5}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {AC} \)
b) \[\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AH} = \frac{2}{3}\,.\,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\]
\[ = \frac{1}{3}\left( {\frac{5}{8}\overrightarrow {AI} + \,\frac{3}{8}\overrightarrow {AJ} + \frac{{25}}{{16}}\overrightarrow {AI} - \,\frac{9}{{16}}\overrightarrow {AJ} } \right)\]
\[ = \frac{{35}}{{48}}\overrightarrow {AI} - \,\frac{1}{{16}}\overrightarrow {AJ} \]
Câu 68:
Cho tam giác ABC.Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI. Hãy phân tích \[\overrightarrow {AI} \]qua hai vectơ \[\overrightarrow {AB} \] và \[\overrightarrow {AC} \]
 Xem đáp án
Xem đáp án
I là điểm trên cạnh BC mà: \[2CI = 3BI \Rightarrow \frac{{BI}}{{CI}} = \frac{2}{3}\]
\( \Rightarrow \frac{{BI}}{{CI + BI}} = \frac{2}{{3 + 2}} \Rightarrow \frac{{BI}}{{BC}} = \frac{2}{5}\)
\( \Rightarrow BI = \frac{2}{5}BC\)
Tương tự ta có: \( \Rightarrow IC = \frac{3}{5}BC\)
J là điểm trên BC kéo dài: \[5JB = 2JC \Rightarrow \frac{{JB}}{{JC}} = \frac{2}{5}\]
\( \Rightarrow \frac{{JB}}{{JC - JB}} = \frac{2}{{5 - 2}} \Rightarrow \frac{{JB}}{{BC}} = \frac{2}{3}\)
\( \Rightarrow JB = \frac{2}{3}BC\)và\(BC = \frac{3}{5}JC\)
Ta có: \(\overrightarrow {AB} = \overrightarrow {AI} + \overrightarrow {IB} = \overrightarrow {AI} - \frac{2}{5}\overrightarrow {BC} = \overrightarrow {AI} - \frac{2}{5}\,.\,\frac{3}{2}\overrightarrow {JB} \)
\( = \overrightarrow {AI} - \,\frac{3}{5}\overrightarrow {JB} = \overrightarrow {AI} - \,\frac{3}{5}\left( {\overrightarrow {JA} + \overrightarrow {AB} } \right) = \overrightarrow {AI} + \,\frac{3}{5}\overrightarrow {AJ} - \,\frac{3}{5}\overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {AB} + \frac{3}{5}\overrightarrow {AB} = \overrightarrow {AI} + \,\frac{3}{5}\overrightarrow {AJ} \)
\( \Rightarrow \overrightarrow {AB} = \frac{5}{8}\overrightarrow {AI} + \,\frac{3}{8}\overrightarrow {AJ} \) (1)
Lại có: \(\overrightarrow {AC} = \overrightarrow {AI} + \overrightarrow {IC} = \overrightarrow {AI} + \frac{3}{5}\overrightarrow {BC} = \overrightarrow {AI} + \frac{3}{5}\,.\,\frac{3}{2}\overrightarrow {JC} \)
\( = \overrightarrow {AI} + \,\frac{9}{{25}}\overrightarrow {JC} = \overrightarrow {AI} + \,\frac{9}{{25}}\left( {\overrightarrow {JA} + \overrightarrow {AB} } \right) = \overrightarrow {AI} - \frac{9}{{25}}\overrightarrow {AJ} + \frac{9}{{25}}\overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {AC} - \frac{9}{{25}}\overrightarrow {AC} = \overrightarrow {AI} - \,\frac{9}{{25}}\overrightarrow {AJ} \)
\( \Rightarrow \overrightarrow {AC} = \frac{{25}}{{16}}\overrightarrow {AI} - \,\frac{9}{{16}}\overrightarrow {AJ} \) (2)
Nhân 2 vế của (1) với \(\frac{3}{2}\) rồi cộng cho vế với vế của (2) ta được:
\(\frac{3}{2}\overrightarrow {AB} + \overrightarrow {AC} = \frac{3}{2}\left( {\frac{5}{8}\overrightarrow {AI} + \,\frac{3}{8}\overrightarrow {AJ} } \right) + \left( {\frac{{25}}{{16}}\overrightarrow {AI} - \,\frac{9}{{16}}\overrightarrow {AJ} } \right)\)
\( = \frac{{15}}{{16}}\overrightarrow {AI} + \frac{9}{{16}}\overrightarrow {AJ} + \frac{{25}}{{16}}\overrightarrow {AI} - \frac{9}{{16}}\overrightarrow {AJ} = \frac{5}{2}\overrightarrow {AI} \)
\( \Rightarrow \overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \)
Câu 69:
Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1,2,3.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 5 chữ số \(\overline {abcde} \;\left( {a \ne b \ne c \ne d \ne e;\;a \ne 0} \right)\)
+) Trường hợp với a là số bất kì kể cả 0
Xếp 3 số 1, 2, 3 vào 3 trong 5 vị trí và sắp xếp có \(A_5^3\) (cách)
Xếp 2 số trong 7 số còn lại vào 2 vị trí còn lại và sắp xếp có \(A_7^2\) (cách)
Suy ra có \(A_5^3\,.\,A_7^2\) số
+) Trường hợp a = 0
Chọn a có 1 cách
Xếp 3 số 1, 2, 3 vào 3 trong 4 vị trí và sắp xếp có \(A_4^3\) (cách)
Xếp 1 số còn lại trong 6 số vào 1 vị trí còn lại có \(C_6^1\) (cách)
Suy ra có \(A_4^3\,.\,C_7^1\) (cách)
Vậy có: \(A_5^3\,.\,A_7^2 - A_4^3\,.\,C_7^1 = 2376\) số thỏa mãn yêu cầu bài toán.
Câu 70:
Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1,2,3 luôn đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 5 chữ số \(\overline {abcde} \;\left( {a \ne b \ne c \ne d \ne e;\;a \ne 0} \right)\)
Buộc 3 chữ số 1, 2, 3 thành 1 cụm, đặt là A
Hoán vị các chữ số 1, 2, 3 cho nhau ta được 3! = 6 khả năng xảy ra của A
Có 3 cách chọn vị trí cho A trong \(\overline {abcde} \)
Sau khi chọn xong vị trí cho A, 2 chữ số còn lại có \(A_7^2 = 42\)cách chọn
Như vậy, sẽ có 3.6.42 = 756 số được tạo thành tính cả trường hợp a = 0.
Xét a = 0:
Khi đó, ta có 2 vị trí cho A, và mỗi vị trí có 6 khả năng xảy ra của A (Hoán vị 1, 2, 3)
Chữ số còn lại có 6 cách chọn
Vậy nếu a = 0 thì sẽ có 72 số được tạo thành.
Vậy, số số tự nhiên có 5 chữ số (a khác 0) thỏa mãn yêu cầu bài toán: 756 − 72 = 684 số tự nhiên.
Câu 71:
 Xem đáp án
Xem đáp án
Gọi chữ số cần tìm là \(\overline {abc} \) (a ≠ 0)
Tổng các chữ số là chẵn khi cả 3 số đều chẵn hoặc 1 số chẵn và 2 số lẻ
TH1: cả 3 số đều chẵn.
Ta thấy a có 4 cách chọn, b có 4 cách chọn, c có 3 cách chọn
Suy ra có 4.4.3 = 48 (cách)
TH2: 2 số lẻ và 1 số chẵn.
• Nếu a chẵn thì a có 4 cách chọn, b có 5 cách chọn, c có 4 cách chọn
Suy ra có 4.5.4 = 80 (cách)
• Nếu a lẻ thì a có 5 cách, b và c lần lượt có (4 . 5 + 5 . 4) cách
Suy ra có 5(4 . 5 + 5 . 4) = 200 (cách).
Tổng cộng có: 48 + 80 + 200 = 328 số thỏa mãn.
Câu 72:
Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Gỉa sử số tự nhiên chẵn gồm 3 chữ số khác nhau là: \(\overline {abc} \) (a ≠ 0)
Khi đó c ∈ {0; 2; 4; 6; 8}
+) Nếu c = 0 có 1 cách chọn
a có 9 cách chọn
b có 8 cách chọn
Suy ra có: 1.9.8 = 72 (số)
+) Nếu c ∈ {2; 4; 6; 8} có 4 cách chọn
a có 8 cách chọn
b có 8 cách chọn
Suy ra có : 4.8.8 = 256 (số)
Vậy số số tự nhiên chẵn gồm 3 chữ số khác nhau là:
72 + 256 = 328 (số)
Câu 73:
Tìm giá trị thực của tham số m khác 0 để y = mx2− 2mx − 3m − 2 có giá trị nhỏ nhất bằng −10 trên ℝ.
 Xem đáp án
Xem đáp án
Ta có: \(x = \frac{{ - b}}{{2a}} = \frac{{2m}}{{2m}} = 1 \Rightarrow y = m\,.\,{1^2} - 2m\,.\,1 - 3m - 2 = - 4m - 2\)
Đỉnh của parabol là I(1; −4m – 2)
Để hàm số có giá trị nhỏ nhất bằng −10 thì:
\(\left\{ \begin{array}{l}a > 0\\{y_I} = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\ - 4m - 2 = - 10\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m = 2\end{array} \right. \Leftrightarrow m = 2\)
Vậy m = 2 là giá trị cần tìm.
Câu 74:
Không thực hiện phép tính,so sánh các tính sau rồi điền dấu >, < hoặc = và viết vào chỗ chấm cho thích hợp:
a) 357,32× 0,34 ....... 35,732 × 3,4; vì ............
b) 491,5× 0,05 ....... 4,915 × 5; vì...............
 Xem đáp án
Xem đáp án
a) 357,32 × 0,34 = 35,732 × 3,4;
Vì 357,32 × 0,34 = 35,732 × 10 × 0,34 = 35,732 × 3,4.
b) 491,5× 0,05 = 4,915 × 5;
Vì 491,5× 0,05 = 4,915 × 100 ×0,05 = 4,915 × 5
Câu 75:
Xét vị trí tương đối của hai đường thẳng d1: x − 2y + 1 = 0 và d2: −3x + 6y – 10 = 0.
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{{ - 3}} = \frac{{ - 2}}{6} \ne \frac{1}{{ - 10}}\).
Suy ra hai đường thẳng đã cho song song với nhau.
Câu 76:
Cho đoạn thẳng AB. Xác định vị trí của điểm C trên đoạn thẳng AB sao cho CA ≤ CB.
 Xem đáp án
Xem đáp án
Xét ba trường hợp:
a) C = M
Ta có: MA = MB nên CA = CB
b) C nằm giữa A và M.
Do C nằm giữa A và M nên CA < MA mà MA = MB nên CA < MB ()
Mặt khác M nằm giữa C và B nên MB < CB (2)
Từ (1) và (2) ta có CA < CB.
c) C nằm giữa M và B
Do C nằm giữa M và B nên CB < MB mà MA = MB nên CB < MA (3)
Mặt khác M nằm giữa A và C nên MA < CA (4)
Từ (3) và (4) ta có: CB < CA.
Vậy nếu điểm C nằm trên đoạn thẳng MA thì ta luôn có CA ≤ CB.
Câu 77:
Giải phương trình: \[\sqrt {x + 1} + 1 = 4{x^2} + \sqrt {3x} \].
 Xem đáp án
Xem đáp án
TXĐ: x ≥ 0
\[\sqrt {x + 1} + 1 = 4{x^2} + \sqrt {3x} \]
\( \Leftrightarrow \sqrt {x + 1} - \sqrt {3x} = 4{x^2} - 1\)
\( \Leftrightarrow \frac{{1 - 2x}}{{\sqrt {x + 1} + \sqrt {3x} }} = \left( {2x - 1} \right)\left( {2x + 1} \right)\)
\( \Leftrightarrow \left( {2x - 1} \right)\left( {2x + 1 + \frac{1}{{\sqrt {x + 1} + \sqrt {3x} }}} \right) = 0\)
Do x ≥ 0 nên suy ra \(2x + 1 + \frac{1}{{\sqrt {x + 1} + \sqrt {3x} }} > 0\)
Vậy phương trình trên có nghiệm 2x − 1 = 0 \( \Leftrightarrow x = \frac{1}{2}\).
Vậy \(x = \frac{1}{2}\) là nghiệm của phương trình.
Câu 78:
Cho a, b, c là độ dài 3 cạnh tam giác. Chứng minh:
\(\frac{{ab}}{{a + b - c}} + \frac{{bc}}{{b + c - a}} + \frac{{ca}}{{c + a - b}} \ge a + b + c\)
 Xem đáp án
Xem đáp án
Đặt: \(\left\{ \begin{array}{l}a + b - c = x\\b + c - a = y\\c + a - b = z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y = 2b\\y + z = 2c\\z + x = 2a\end{array} \right.\)
Do a, b, c là độ dài 3 cạnh tam giác nên x; y; z > 0
Ta có: \[A = \frac{{ab}}{{a + b - c}} + \frac{{bc}}{{b + c - a}} + \frac{{ca}}{{c + a - b}}\]
\[ \Rightarrow 4A = \frac{{2a\,.\,2b}}{{a + b - c}} + \frac{{2b\,.\,2c}}{{b + c - a}} + \frac{{2c\,.\,2a}}{{c + a - b}}\]
\[ = \frac{{\left( {z + x} \right)\left( {x + y} \right)}}{x} + \frac{{\left( {x + y} \right)\left( {y + z} \right)}}{y} + \frac{{\left( {y + z} \right)\left( {z + x} \right)}}{z}\]
\[ = 3\left( {x + y + z} \right) + \left( {\frac{{yz}}{x} + \frac{{zx}}{y} + \frac{{xy}}{z}} \right)\]
\[ \ge 3\left( {x + y + z} \right) + \frac{{\left( {x + y + z} \right)xyz}}{{xyz}}\]
= 4(x + y + z) = 4(a + b + c)
Do a; b; c > 0 nên suy ra A ≥ a + b + c (đpcm).
Câu 79:
Cho a, b, c là độ dài 3 cạnh tam giác. Chứng minh:
\(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).
 Xem đáp án
Xem đáp án
Đặt: \(\left\{ \begin{array}{l}b + c - a = x\\a + c - b = y\\a + b - c = z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y = 2c\\y + z = 2a\\z + x = 2b\end{array} \right.\)
Do a, b, c là độ dài 3 cạnh tam giác nên x, y, z > 0
Ta có:
\[A = \frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}}\]
\[ \Rightarrow 2A = \frac{{2a}}{{b + c - a}} + \frac{{2b}}{{a + c - b}} + \frac{{2c}}{{a + b - c}}\]
\[ = \frac{{y + z}}{x} + \frac{{z + x}}{y} + \frac{{x + y}}{z}\]
\[ = \frac{y}{x} + \frac{z}{x} + \frac{z}{y} + \frac{x}{y} + \frac{x}{z} + \frac{y}{z}\]
\[ = \left( {\frac{y}{x} + \frac{x}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) + \left( {\frac{z}{y} + \frac{y}{z}} \right)\]
Dễ chứng minh \(\frac{a}{b} + \frac{b}{a} \ge 2\sqrt {\frac{a}{b}\,.\,\frac{b}{a}} = 2\;\left( {a;\;b > 0} \right)\) (BĐT AG – GM)
\( \Rightarrow 2A = \left( {\frac{y}{x} + \frac{x}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) + \left( {\frac{z}{y} + \frac{y}{z}} \right) \ge 2 + 2 + 2 = 6\)
\( \Rightarrow A = \frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\)(đpcm).
Câu 80:
Một thửa ruộng hình chữ nhật có chiều dài 60m, chiều dài bằng \(\frac{3}{2}\) chiều rộng, trên thửa ruộng đó người ta trồng lúa cứ 100m2 thu hoạch được 50 kg. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ thóc?
 Xem đáp án
Xem đáp án
Chiều rộng của thửa ruộng là:
\[60:\frac{3}{2} = 40\;\left( m \right)\]
Diện tích của thửa ruộng là:
60 × 40 = 2 400 (m2)
Trên cả thửa ruộng thu hoạch được là:
2400 : 100 × 50 = 1 200 (kg) = 12 (tạ)
Đáp số:12 tạ thóc
Câu 81:
Thửa ruộng hình chữ nhật có chiều dài 60 m, chiều rộng bằng \(\frac{2}{3}\) chiều dài. Trung bình cứ 100 mét vuông thì thu hoạch được 50 kg thóc. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu ki-lô-gam thóc?
 Xem đáp án
Xem đáp án
Chiều rộng của thửa ruộng là:
\[60 \times \frac{2}{3} = 40\;\left( m \right)\]
Diện tích của thửa ruộng là:
60 × 40 = 2 400 (m2)
Trên cả thửa ruộng thu hoạch được là:
2400 : 100 × 50 = 1 200 (kg) = 12 (tạ)
Đáp số: 1 200 kg thóc
Câu 82:
Cho các chữ số 0, 1, 2, 3, 4. Hỏi có thể lập được bao nhiêu số tự nhiên có 7 chữ số, trong đó chữ số 4 có mặt đúng 3 lần, các chữ số còn lại có mặt đúng 1 lần?
 Xem đáp án
Xem đáp án
• Bước 1: Tìm số lượng tất cả các số được tạo bởi bao gồm trường hợp chữ số 0 ở đầu
Ta có:
Số cách sắp xếp vị trí cho 3 chữ số 4 là: \[C_7^3 = 35\]
Số cách sắp xếp vị trí cho 4 chữa số 0,1,2,3 là: \(P_4^4 = 4! = 24\)
Suy ra có 35.24 = 840 (số)
• Bước 2: Tìm số lượng số có chữ số 0 ở đầu
Ta có:
Số cách sắp xếp vị trí cho 3 chữ số 4 ở 6 vị trí còn lại là: \[C_6^3 = 20\]
Số cách sắp xếp vị trí cho 3 chữa số 1, 2, 3 ở 3 vị trí còn lại là:
\(P_3^3 = 3! = 6\)
Suy ra có: 20.6 = 120 (số)
Vậy số lượng số cần tìm bằng:
840 – 120 = 720 (số)
Câu 83:
Từ các chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số: Có 8 chữ số trong đó chữ số 1có mặt 3 lần, chữ số 4 xuất hiện 2 lần; các chữ số còn lại có mặt đúng một lần.
 Xem đáp án
Xem đáp án
Xếp số vào 8 ô trống thỏa yêu cầu Đề bài.
Bước 1: Chọn 3 ô trong 8 ô để xếp 3 chữ số 1, có \(C_8^3\) cách.
Bước 2: Chọn 2 ô trong 5 ô còn lại để xếp 2 chữ số 4, có \(C_5^2\) cách.
Bước 3: Xếp 3 chữ số số còn lại vào 3 ô còn lại, có 3! cách.
Vậy có \[C_8^3\,.\,C_5^2\,.\,3!\] số thỏa yêu cầu, nhưng có những số có chữ số 0 đứng vị trí đầu tiên.
Trường hợp số 0 ở ô thứ nhất.
Bước 1: Chọn 3 ô trong 7 ô còn lại, xếp 3 chữ số 1, có \(C_7^3\) cách.
Bước 2: Chọn 2 ô trong 4 ô còn lại, xếp 2 chữ số 4, có \(C_4^2\) cách.
Bước 3: Xếp hai chữ số còn lại vào 2 ô còn lại, có 2! cách.
Vậy có: \[C_7^3\,.\,C_4^2\,.\,3!\] số mà chữ số 0 ở vị trí đầu tiên.
Kết luận có: \[C_8^3\,.\,C_5^2\,.\,3! - C_7^3\,.\,C_4^2\,.\,3! = 2940\] số thỏa yêu cầu.
Vậy ta chọn đáp án C.
Câu 84:
Giải phương trình: 2x + 1 − 2x = 32.
 Xem đáp án
Xem đáp án
Ta có: 2x + 1 − 2x = 32
Û 2x(2 – 1) = 32
Û 2x = 32
Û 2x = 25
Û x = 5
Vậy x = 5 là nghiệm của phương trình.
Câu 85:
Giải phương trình: 22x + 1 = 32.
 Xem đáp án
Xem đáp án
Ta có: 22x + 1 = 32
Û 22x + 1 = 25
Û 2x + 1 = 5
Û x = 2
Vậy x = 2 là nghiệm của phương trình.
