Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:
a) y = x4 - 2x2 + 1 ;
b) y = sin2x – x
c) y = sinx + cosx ;
d) y = x5 - x3 - 2x + 1
 Giải bởi Vietjack
Giải bởi Vietjack
a) TXĐ: D = R.
+ y' = 4x3 - 4x
y' = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 hoặc x = ±1.
+ y" = 12x2 - 4
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.
y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.
y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.
b) TXĐ: D = R
+ y' = 2cos2x – 1;
+ y" = -4.sin2x
⇒ 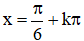
⇒ 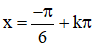
c) TXĐ: D = R
+ y’ = cos x – sin x.
+ y’’ = -sin x – cos x =
⇒ 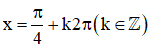
⇒ 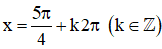
d) TXĐ: D = R
+ y'= 5x4 - 3x2 - 2
y' = 0 ⇔ 5x4 – 3x2 – 2 = 0
⇔ x = ±1.
+ y" = 20x3 - 6x
y"(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y"(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
Kiến thức áp dụng
Tìm điểm cực trị của hàm số :
1. Tìm tập xác định
2. Tính f’(x). Tìm các giá trị xi để f’(x) = 0 hoặc f’(x) không xác định.
3. Tính f’’(x). Xét dấu f’’(xi).
4. Kết luận : Các điểm xi làm cho f’’(xi) < 0 là các điểm cực đại
Các điểm xi làm cho f’’(xi) > 0 là các điểm cực tiểu.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 - 36x - 10
Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?
Chứng minh hàm số y = không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Xác định giá trị của tham số m để hàm số m để hàm số đạt giá trị cực đại tại x = 2.
Tìm a và b để các cực trị của hàm số
đều là nhưng số dương và xo = -5/9 là điểm cực đại.
Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 - mx2 - 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
a) y = -x2 + 1 trong khoảng (-∞; +∞);
b) y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4).
a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.
• y = -2x + 1;
• y = x/3(x-3)2 (H.8).
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).