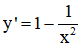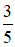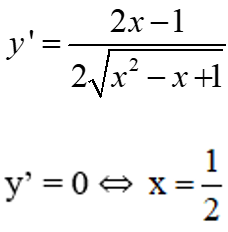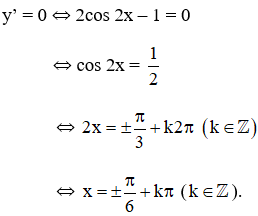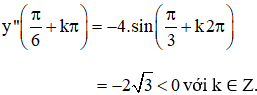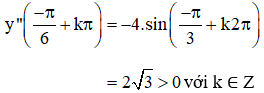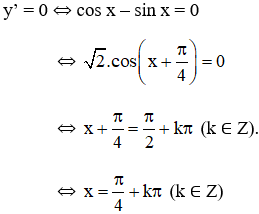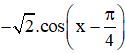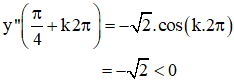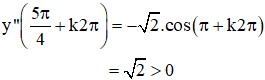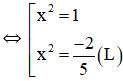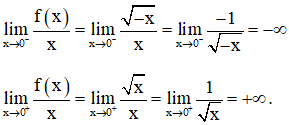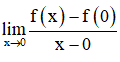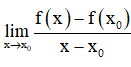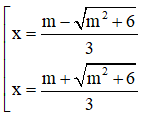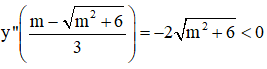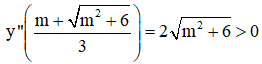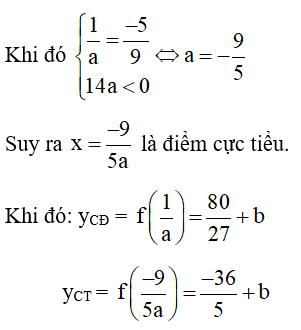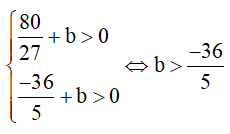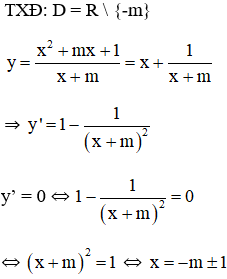11 câu hỏi trắc nghiệm thuộc Bài 2: Cực trị của hàm số

Câu 1:

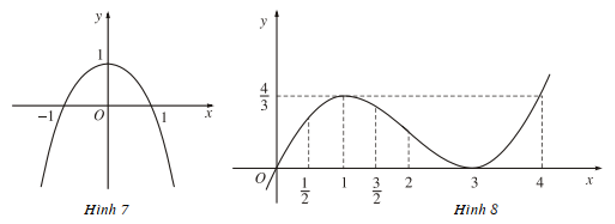
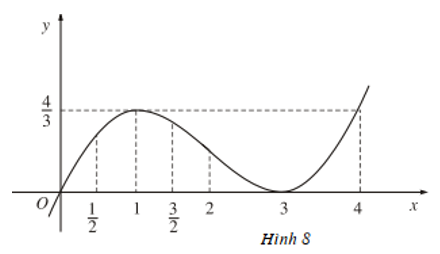
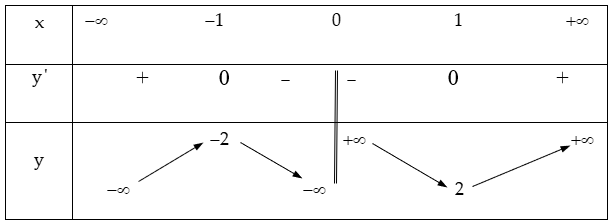
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):

a) y = -x² + 1 trong khoảng (-∞; +∞);

b) y = x/3(x+ 3)² trong các khoảng (1/2; 3/2) và (3/2; 4).

Xem đáp án

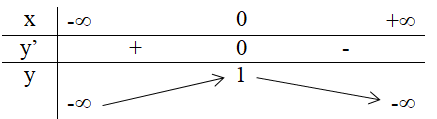
a) Tại x = 0 hàm số có giá trị lớn nhất bằng 1.

Xét dấu đạo hàm:

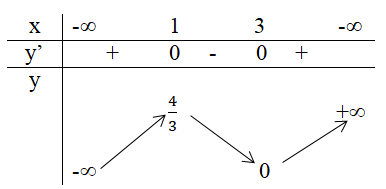
b) Tại x = 1 hàm số có giá trị lớn nhất bằng 4/3.

Tại x = 3 hàm số có giá trị nhỏ nhất bằng 0.

Xét dấu đạo hàm:

Câu 2:

Giả sử f(x) đạt cực đại tại x_o. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số $\frac{f (x_{0} + ∆ x) - f (x_{0})}{∆ x}$ khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.

Xem đáp án

Với Δx > 0 Ta có 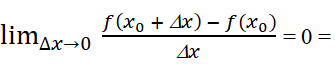f'(x_o⁺ ).

Với Δx < 0 Ta có 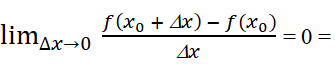f'(x_o^- ).

Vậy f’(x_o) = 0.

Câu 3:

a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.

• y = -2x + 1;

• y = x/3(x-3)² (H.8).

b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.

Xem đáp án

a,Hàm số y = -2x + 1 không có cực trị.

Hàm số y = x/3 (x-3)² đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.

b, Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.

Câu 4:

Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?

Xem đáp án

Vậy không tồn tại đạo hàm của hàm số tại x = 0.

Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.

Câu 5:

Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).

Xem đáp án

1. TXĐ: D = R

2. f’(x) = 3x^2 – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.

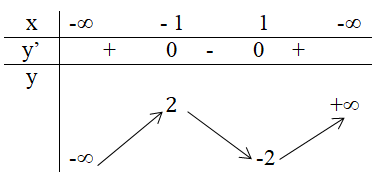
3. Ta có bảng biến thiên:

Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2

Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2.

Câu 6:

Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:

a) y = 2x³ + 3x² - 36x - 10

$b) y = x^{4} + 2 x^{2} - 3; c) y = x + \frac{1}{x}; d) y = x^{3} {(1 - x)}^{2}; e) y = \sqrt{x^{2} - x + 1}$

Xem đáp án

a) TXĐ: D = R

y' = 6x² + 6x - 36

y' = 0 ⇔ x = -3 hoặc x = 2

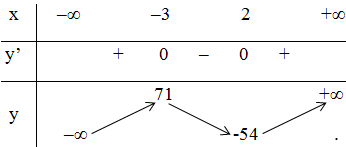
Bảng biến thiên:

Kết luận :

Hàm số đạt cực đại tại x = -3 ; y_CĐ = 71

Hàm số đạt cực tiểu tại x = 2; y_CT = -54.

b) TXĐ: D = R

y'= 4x³ + 4x = 4x(x² + 1) = 0;

y' = 0 ⇔ x = 0

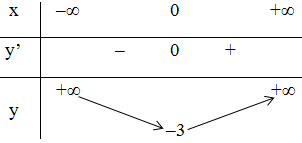
Bảng biến thiên:

Vậy hàm số đạt cực tiểu tại x = 0; y_CT = -3

hàm số không có điểm cực đại.

c) TXĐ: D = R \ {0}

y' = 0 ⇔ x = ±1

Bảng biến thiên:

Vậy hàm số đạt cực đại tại x = -1; y_CĐ = -2;

hàm số đạt cực tiểu tại x = 1; y_CT = 2.

d) TXĐ: D = R

y'= (x³)’.(1 – x)² + x³.[(1 – x)²]’

= 3x².(1 – x)² + x³.2(1 – x).(1 – x)’

= 3x²(1 – x)² - 2x³(1 – x)

= x².(1 – x)(3 – 5x)

y' = 0 ⇔ x = 0; x = 1 hoặc x = 3/5

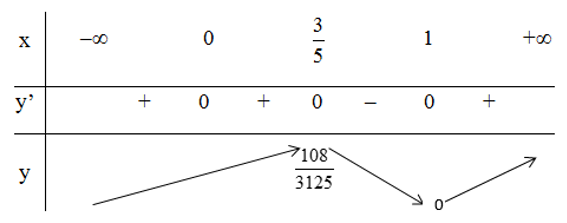
Bảng biến thiên:

Vậy hàm số đạt cực đại tại x =

hàm số đạt cực tiểu tại x_CT = 1.

(Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)

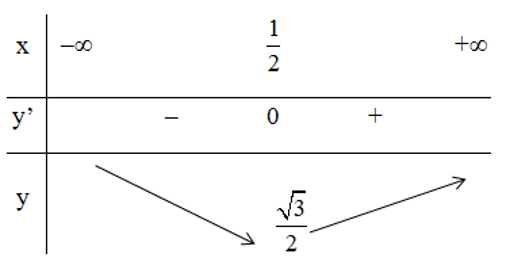
e) Tập xác định: D = R.

Bảng biến thiên:

Vậy hàm số đạt cực tiểu tại x = 1/2.

Kiến thức áp dụng

Quy tắc tìm điểm cực trị của hàm số y = f(x).

1. Tìm tập xác định.

2. Tính f’(x). Xác định các điểm thỏa mãn f’(x) = 0 hoặc f’(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra điểm cực trị.

(Điểm cực trị là các điểm làm cho f’(x) đổi dấu khi đi qua nó).

Câu 7:

Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:

a) y = x⁴ - 2x² + 1 ;

b) y = sin2x – x

c) y = sinx + cosx ;

d) y = x⁵ - x³ - 2x + 1

Xem đáp án

a) TXĐ: D = R.

+ y' = 4x³ - 4x

y' = 0 ⇔ 4x(x² – 1) = 0 ⇔ x = 0 hoặc x = ±1.

+ y" = 12x² - 4

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.

y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.

y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.

b) TXĐ: D = R

+ y' = 2cos2x – 1;

+ y" = -4.sin2x

⇒ (k ∈ Z) là các điểm cực đại của hàm số.

⇒ (k ∈ Z) là các điểm cực tiểu của hàm số.

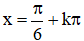
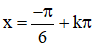
c) TXĐ: D = R

+ y’ = cos x – sin x.

+ y’’ = -sin x – cos x =

⇒ là các điểm cực đại của hàm số.

⇒ là các điểm cực tiểu của hàm số.

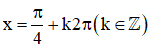
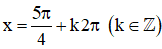
d) TXĐ: D = R

+ y'= 5x⁴ - 3x² - 2

y' = 0 ⇔ 5x⁴ – 3x² – 2 = 0

⇔ x = ±1.

+ y" = 20x³ - 6x

y"(-1) = -20 + 6 = -14 < 0

⇒ x = -1 là điểm cực đại của hàm số.

y"(1) = 20 – 6 = 14 > 0

⇒ x = 1 là điểm cực tiểu của hàm số.

Kiến thức áp dụng

Tìm điểm cực trị của hàm số :

1. Tìm tập xác định

2. Tính f’(x). Tìm các giá trị x_i để f’(x) = 0 hoặc f’(x) không xác định.

3. Tính f’’(x). Xét dấu f’’(x_i).

4. Kết luận : Các điểm x_i làm cho f’’(x_i) < 0 là các điểm cực đại

Các điểm x_i làm cho f’’(x_i) > 0 là các điểm cực tiểu.

Câu 8:

Chứng minh hàm số y = $\sqrt{|x|}$ không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.

Xem đáp án

Hàm số có tập xác định D = R và liên tục trên R.

+ Chứng minh hàm số 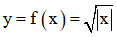không có đạo hàm tại x = 0.

Xét giới hạn :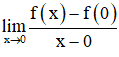

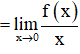
⇒ Không tồn tại giới hạn

Hay hàm số không có đạo hàm tại x = 0.

+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).

Ta có : f(x) > 0 = f(0) với ∀ x ∈ (-1 ; 1) và x ≠ 0

⇒ Hàm số y = f(x) đạt cực tiểu tại x = 0.

Kiến thức áp dụng

Hàm số y = f(x) liên tục trên (a ; b) và x₀ ∈ (a ; b).

+ Hàm số y = f(x) có đạo hàm tại x₀ nếu tồn tại giới hạn

+ Hàm số y = f(x) đạt cực tiểu tại x₀ nếu tồn tại số dương h sao cho f(x) > f(x₀) với ∀ x ∈ (x₀ – h ; x₀ + h) và x ≠ x₀.

Câu 9:

Chứng minh rằng với mọi giá trị của tham số m, hàm số

y = x³ - mx² - 2x + 1

luôn luôn có một cực đại và một điểm cực tiểu.

Xem đáp án

TXĐ: D = R

+ y' = 3x² - 2mx – 2

y’ = 0 ⇔ 3x² – 2mx – 2 = 0 ⇔

+ y’’ = 6x – 2m.

⇒ là một điểm cực đại của hàm số.

⇒ là một điểm cực tiểu của hàm số.

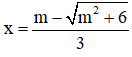
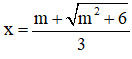
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.

Kiến thức áp dụng

Xét y = f(x) có đạo hàm cấp hai trong khoảng (x₀ – h ; x₀ + h), h > 0.

+ f’(x₀) = 0 và f’’(x₀) > 0 thì x₀ là điểm cực tiểu.

+ f’(x₀) = 0 và f’’(x₀) < 0 thì x₀ là điểm cực đại.

Câu 10:

Tìm a và b để các cực trị của hàm số

$y = \frac{5}{3} a^{2} x^{3} + 2 a x^{2} - 9 x + b$

đều là nhưng số dương và x_o = -5/9 là điểm cực đại.

Xem đáp án

TXĐ: D = R.

+ y’ = 5a²x² + 4ax – 9.

⇒ y’’ = 10a²x + 4a.

- Nếu a = 0 thì y’ = -9 < 0 với ∀ x ∈ R

⇒ Hàm số không có cực trị (loại)

- Nếu a ≠ 0.

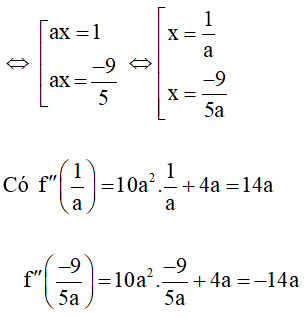
Các cực trị của hàm số đều dương

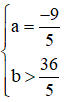
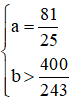
Vậy hoặc là các giá trị cần tìm.

Kiến thức áp dụng

Xét y = f(x) có đạo hàm cấp hai trong khoảng (x₀ – h ; x₀ + h), h > 0.

+ f’(x₀) = 0 và f’’(x₀) > 0 thì x₀ là điểm cực tiểu.

+ f’(x₀) = 0 và f’’(x₀) < 0 thì x₀ là điểm cực đại.

Câu 11:

Xác định giá trị của tham số m để hàm số m để hàm số $y = \frac{x^{2} + m x + 1}{x + m}$ đạt giá trị cực đại tại x = 2.

Xem đáp án

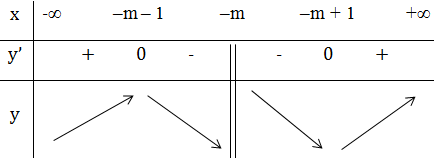
Ta có bảng biến thiên:

Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.

Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.

Vậy m = -3.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Bài 2: Cực trị của hàm số

Danh sách câu hỏi

Bài thi liên quan