Giải sách bài tập Toán lớp 10 Bài tập cuối chương 1

A. Trắc nghiệm

Bài 1 trang 18 SBT Toán 10 Tập 1: Mệnh đề nào sau đây đúng?

A. 0 = {0};

B. 0 ∈ {0};

C. 0 ⊂ {0};

D. 0 = ∅.

Lời giải:

Đáp án đúng là: B

Ta có {0} là một tập hợp, 0 là một phần tử nên viết 0 = {0} là sai, do đó đáp án A sai.

0 là một phần tử của tập hợp {0}, do đó ta viết 0 ∈ {0} là đúng nên đáp án B đúng.

Kí hiệu ⊂ dùng để chỉ mối quan hệ giữa các tập hợp nên đáp án C sai.

∅ là một tập hợp nên đáp án D sai.

Bài 2 trang 18 SBT Toán 10 Tập 1: Biết rằng P ⇒ Q là mệnh đề đúng. Mệnh đề nào sau đây đúng?

A. P là điều kiện cần để có Q;

B. P là điều kiện đủ để có Q;

C. Q là điều kiện cần và đủ để có P;

D. Q là điều kiện đủ để có P.

Lời giải:

Đáp án đúng là: B

Ta có P ⇒ Q là mệnh đề đúng, khi đó, ta có thể nói bằng một trong các cách sau:

+ P suy ra Q;

+ P kéo theo Q;

+ P là điều kiện đủ để có Q;

+ Q là điều kiện cần để có P.

Vậy trong các đáp án đã cho, đáp án B là đáp án đúng.

Bài 3 trang 18 SBT Toán 10 Tập 1: Cho số thực x. Mệnh đề nào sau đây là điều kiện đủ của “x > 1”?

A. x > 0;

B. x ≥ 1;

C. x < 1;

D. x ≥ 2.

Lời giải:

Đáp án đúng là: D

Ta có P ⇒ Q là mệnh đề đúng thì P là điều kiện đủ để có Q.

Xét các mệnh đề:

+ “Nếu x > 0 thì x > 1”, đây là mệnh đề sai, chẳng hạn ta có thể lấy x = 1, có 1 > 0 đúng nhưng 1 > 1 sai.

+ “Nếu x ≥ 1 thì x > 1”, đây là mệnh đề sai, chẳng hạn ta có thể lấy x = 1, có 1 ≥ 1 đúng nhưng 1 > 1 sai.

+ “Nếu x < 1 thì x > 1”, đây là mệnh đề sai.

+ “Nếu x ≥ 2 thì x > 1”, đây là mệnh đề đúng do 2 > 1.

Vậy mệnh đề “x ≥ 2” là điều kiện đủ của “x > 1”.

Bài 4 trang 18 SBT Toán 10 Tập 1: Mệnh đề nào sau đây sai?

(1) ∅ ∈ {0};

(2) {1} ⊂ {0; 1; 2};

(3) {0} = ∅;

(4) {0} ⊂ {x | x² = x}.

A. (1) và (3);

B. (1) và (4);

C. (2) và (4);

D. (2) và (3).

Lời giải:

Đáp án đúng là: A

Ta có: ∅ và {0} đều là các tập hợp, mà kí hiệu ∈ dùng để chỉ mối quan hệ giữa phần tử và tập hợp nên mệnh đề (1) sai.

Tập hợp {1} gồm một phần tử là 1, phần tử này thuộc tập {0; 1; 2} nên {1} ⊂ {0; 1; 2}, do đó mệnh đề (2) đúng.

Tập ∅ không chứa phần tử nào, tập {0} chứa một phần tử 0, nên hai tập này không thể bằng nhau, do đó mệnh đề (3) sai.

Ta có: x² = x ⇔ x = 0 hoặc x = 1, do đó {x | x² = x} = {0; 1}.

Có {0} ⊂ {0; 1}, từ đó suy ra {0} ⊂ {x | x² = x} nên mệnh đề (4) đúng.

Vậy trong các mệnh đề đã cho, mệnh đề (1) và (3) là mệnh đề sai.

Bài 5 trang 18 SBT Toán 10 Tập 1: Cho tập hợp M = {x ∈ ℕ | x = 5 – m, m ∈ ℕ}. Số phần tử của tập hợp M bằng:

A. 4;

B. 5;

C. 6;

D. 10.

Lời giải:

Đáp án đúng là: C

Do m và x là các số tự nhiên, nên ta lần lượt thay các giá trị của m bởi 0, 1, 2,... để tìm x thỏa mãn.

Ta có:

Với m = 0 thì x = 5 – 0 = 5 ∈ ℕ;

Với m = 1 thì x = 5 – 1 = 4 ∈ ℕ;

Với m = 2 thì x = 5 – 2 = 3 ∈ ℕ;

Với m = 3 thì x = 5 – 3 = 2 ∈ ℕ;

Với m = 4 thì x = 5 – 4 = 1 ∈ ℕ;

Với m = 5 thì x = 5 – 5 = 0 ∈ ℕ;

Với m = 6 thì x = 5 – 6 = – 1 ∉ ℕ, không thỏa mãn, ta dừng lại.

Vậy các giá trị x thỏa mãn là 0, 1, 2, 3, 4, 5.

Do đó, M = {0; 1; 2; 3; 4; 5} nên tập hợp M có 6 phần tử.

Bài 6 trang 18 SBT Toán 10 Tập 1: Tập hợp {y ∈ ℕ | y = 5 – $x^2$, x ∈ ℕ} có bao nhiêu tập hợp con?

A. 3;

B. 4;

C. 8;

D. 16.

Lời giải:

Đáp án đúng là: C

Do y và x là các số tự nhiên, nên ta lần lượt thay các giá trị của x bởi 0, 1, 2,... để tìm y thỏa mãn. 

Ta có:

Với x = 0 thì y = 5 – 0² = 5 ∈ ℕ;

Với x = 1 thì y = 5 – 1² = 4 ∈ ℕ;

Với x = 2 thì y = 5 – 2² = 1 ∈ ℕ;

Với x = 3 thì y = 5 – 3² = – 4 ∉ ℕ, không thỏa mãn, ta dừng lại.

Vậy các giá trị y thỏa mãn là 1, 4, 5.

Do đó, {y ∈ ℕ | y = 5 – x², x ∈ ℕ} = {1; 4; 5}.

Các tập con của tập hợp {1; 4; 5} là ∅, {1}, {4}, {5}, {1; 4}, {1; 5}, {4; 5}, {1; 4; 5}.

Vậy có 8 tập con thỏa mãn.

Ngoài ra, ta có thể tính số tập con của một tập gồm k phần tử bằng cách tính 2^k.

Tập {1; 4; 5} có 3 phần tử nên có 2³ = 8 tập con.

Bài 7 trang 18 SBT Toán 10 Tập 1: Cho A = {– 2; – 1; 0; 1; 2}, B = {x | x + 1 ≤ 0}. Tập hợp A \ B bằng

A. {0; 1; 2};

B. {– 1};

C. {– 2; – 1};

D. {– 2}.

Lời giải:

Đáp án đúng là: A

Ta có: x + 1 ≤ 0 ⇔ x ≤ 0 – 1 ⇔ x ≤ – 1.

Do đó, B = {x | x + 1 ≤ 0} = {x | x ≤ – 1} = (– ∞; – 1].

Vậy A \ B = {– 2; – 1; 0; 1; 2} \ (– ∞; – 1] = {0; 1; 2}.

Bài 8 trang 18 SBT Toán 10 Tập 1: Cho các tập hợp A = {– 1; 0; 1; 2}, B = {x | x – 1 ≥ 0}. Tập hợp A \ B bằng

A. {2};

B. {– 1; 0; 1};

C. {1; 2};

D. {– 1; 0}.

Lời giải:

Đáp án đúng là: D

Ta có: x – 1 ≥ 0 ⇔ x ≥ 1.

Do đó, B = {x | x – 1 ≥ 0} = {x | x ≥ 1} = [1; + ∞).

Vậy A \ B = {– 1; 0; 1; 2} \ [1; + ∞) = {– 1; 0}.

Bài 9 trang 18 SBT Toán 10 Tập 1: Cho A = {x | x là hình bình hành}, B = {x | x là hình chữ nhật}, C = {x | x là hình thoi}, D = {x | x là hình vuông}. Mệnh đề nào sau đây sai?

A. B ∩ C = D;

B. C ∩ D = D;

C. B ∪ C = D;

D. B ∩ D = D.

Lời giải:

Đáp án đúng là: C

Lấy phần tử a tùy ý thuộc D, khi đó a là một hình vuông, mà hình vuông có 4 góc bằng nhau và bằng 90° nên nó cũng là hình chữ nhật, do đó a thuộc B.

Vậy D ⊂ B nên B ∩ D = D, đáp án D đúng.

Tương tự hình vuông thì có 4 cạnh bằng nhau nên nó cũng là một hình thoi, do đó a thuộc C. Vậy D ⊂ C nên C ∩ D = D, đáp án B đúng.

Hình thoi có 4 cạnh bằng nhau, hình chữ nhật có 4 góc bằng nhau và bằng 90°, do đó một hình vừa là hình chữ nhật vừa là hình thoi thì nó sẽ là hình vuông nên B ∩ C = D, đáp án A đúng.

Đáp án C sai do nếu ta có B ∪ C = D, x ∈ B ∪ C thì x ∈ D. Có x ∈ B ∪ C thì x là hình chữ nhật hoặc hình thoi, mà hình chữ nhật hoặc hình thoi thì chưa chắc đã là hình vuông nên vô lí.

Bài 10 trang 18 SBT Toán 10 Tập 1: Cho tập hợp A = {x | x > a}, B = {x | 1 < x < 2}. Để A ∪ (C_ℝB) = ℝ, điều kiện cần và đủ là

A. a ≤ 1;

B. a < 1;

C. a ≥ 2;

D. a > 2

Lời giải:

Đáp án đúng là: B

Ta có: A = {x | x > a} = (a; + ∞).

B = {x | 1 < x < 2} = (1; 2).

Lại có C_ℝB = ℝ \ B = (– ∞; 1] ∪ [2; + ∞). 

Để A ∪ (C_ℝB) = ℝ thì (a; + ∞) ∪ (– ∞; 1] ∪ [2; + ∞) = ℝ.

Từ đó suy ra a < 1.

B. Tự luận

Bài 1 trang 19 SBT Toán 10 Tập 1: Cho ba tập hợp A, B, C thỏa mãn A ⊂ C, B ⊂ C và A ∩ B = ∅. Xét tính đúng sai của các mệnh đề sau.

a) Nếu x ∈ A thì x ∈ C;

b) x ∈ A là điều kiện cần để x ∈ C;

c) x ∈ B là điều kiện đủ để x ∈ C;

d) Nếu x ∈ A thì x ∉ B;

e) x ∈ B là điều kiện đủ để x ∉ A.

Lời giải:

a) Vì A ⊂ C nên mọi phần tử của A đều là phần tử của C nên x ∈ A thì x ∈ C, mệnh đề a) đúng.

b) Mệnh đề “Nếu x ∈ A thì x ∈ C” là mệnh đề đúng (theo câu a), do đó, “x ∈ A là điều kiện đủ để x ∈ C”, vậy b) sai.

c) Vì B ⊂ C nên mọi phần tử của B đều là phần tử của C nên x ∈ B thì x ∈ C, ta có mệnh đề đúng là “Nếu x ∈ B thì x ∈ C” hay “x ∈ B là điều kiện đủ để x ∈ C”, do đó c) đúng.

d) Do A ∩ B = ∅, nên A và B là hai tập rời nhau hay mọi phần tử của A đều khác các phần tử trong B, khi đó ta có “Nếu x ∈ A thì x ∉ B” là mệnh đề đúng, vậy d) đúng.

e) Do A ∩ B = ∅, nên A và B là hai tập rời nhau hay mọi phần tử của A đều khác các phần tử trong B, khi đó ta có “Nếu x ∈ B thì x ∉ A” là mệnh đề đúng, do đó mệnh đề còn được phát biểu dưới dạng “x ∈ B là điều kiện đủ để x ∉ A”, vậy e) đúng.

Bài 2 trang 19 SBT Toán 10 Tập 1: Cho tập hợp A = {1; 2}. Tìm tất cả các tập hợp B thỏa mãn A ∪ B = {1; 2; 3}.

Lời giải:

Ta có: A = {1; 2} và A ∪ B = {1; 2; 3}, mà 3 ∉ A, do đó 3 ∈ B, hơn nữa B ⊂ {1; 2; 3}.

Do đó, B là các tập con chứa phần tử 3 của tập {1; 2; 3}, đó là các tập: {3}, {1; 3}, {2; 3}, {1; 2; 3}.

Vậy các tập hợp B thỏa mãn yêu cầu là: {3}, {1; 3}, {2; 3}, {1; 2; 3}.

Bài 3 trang 19 SBT Toán 10 Tập 1: Cho hai tập hợp A = {1; 2; 3; 4}, B = {3; 4; 5}. Tìm tất cả các tập hợp M thỏa mãn M ⊂ A và M ∩ B = ∅.

Lời giải:

Do M ∩ B = ∅ nên M và B là hai tập hợp rời nhau hay mọi phần tử của tập hợp M đều khác các phần tử trong tập hợp B, do đó tập hợp M không chứa các phần tử 3; 4; 5. (1)

Lại có M ⊂ A, do đó mọi phần tử của M đều là phần tử của A nên M có thể chứa các phần tử 1; 2; 3; 4. (2).

Từ (1) và (2) suy ra M chỉ có thể chứa các phần tử 1; 2.

Do đó, M = {1}, M = {2}, M = {1; 2}.

Lại có ∅ ⊂ A và ∅ ∩ B = ∅, do đó M = ∅.

Vậy các tập hợp M thỏa mãn là: ∅, {1}, {2}, {1; 2}.

Bài 4 trang 19 SBT Toán 10 Tập 1: Một học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn và 10 người không thích môn nào trong hai môn thể thao này.

a) Có bao nhiêu học sinh của thích cả hai môn trên?

b) Có bao nhiêu học sinh của thích bóng rổ nhưng không thích bóng bàn?

Lời giải:

Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},

C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.

Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.

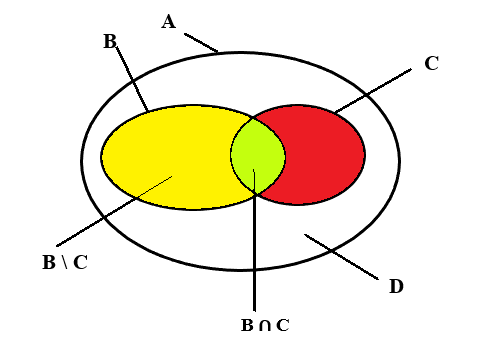
a) Số học sinh thích một trong hai môn là:

n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).

Số học sinh thích cả hai môn thể thao trên là:

n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).

b) Số học sinh thích bóng rổ nhưng không thích bóng bàn là:

n(B \ C) = n(B) – n(B ∩ C) = 20 – 8 = 12 (bạn).