Giải sách bài tập Toán lớp 10 Bài 1: Khái niệm vectơ

Bài 1 trang 91 SBT Toán 10 Tập 1: Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

- Chiếc xe máy có giá tiền là 30 triệu đồng.

- Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam.

Lời giải:

- Chiếc xe máy có giá tiền là 30 triệu đồng: đại lượng vô hướng.

- Chiếc thuyền chạy với vận tốc là 30 km/h theo hướng tây nam: đại lượng chỉ rõ giá trị và hướng.

Bài 2 trang 91 SBT Toán 10 Tập 1: Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?

Nhiệt độ, lực, thể tích, tuổi, độ dịch chuyển, vận tốc.

Lời giải:

Các đại lượng cần được biểu diễn bởi vectơ: lực, độ dịch chuyển, vận tốc bởi đây là những đại lượng có hướng.

Bài 3 trang 91 SBT Toán 10 Tập 1: Cho hình thang ABCD với hai đáy là AB, CD và có hai đường chéo cắt nhau tại O.

a) Gọi tên hai vectơ cùng hướng với $\overrightarrow{\text{AO}}$.

b) Gọi tên hai vectơ ngược hướng với $\overrightarrow{\text{AB}}$.

Lời giải:

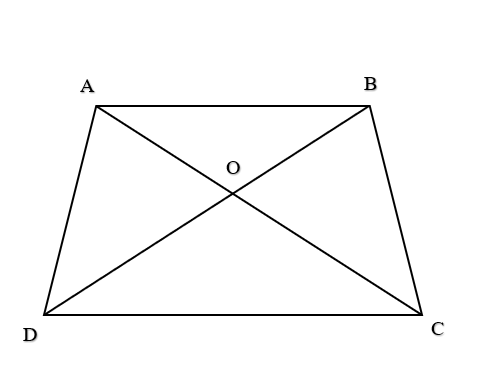
a) Hai vectơ cùng hướng với $\overrightarrow{\text{AO}}$: $\overrightarrow{\text{AC}}$ và $\overrightarrow{\text{OC}}$.

b) Hai vectơ ngược hướng với $\overrightarrow{\text{AB}}$: $\overrightarrow{\text{BA}}$ và $\overrightarrow{\text{CD}}$.

Bài 4 trang 91 SBT Toán 10 Tập 1: Cho hình thoi ABCD cạnh bằng a có tâm O và $\widehat{\text{BAD}}$ = 60°.

a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng $\frac{\text{a}\sqrt{\text{3}}}{\text{2}}$.

b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng a$\sqrt{3}$.

Lời giải:

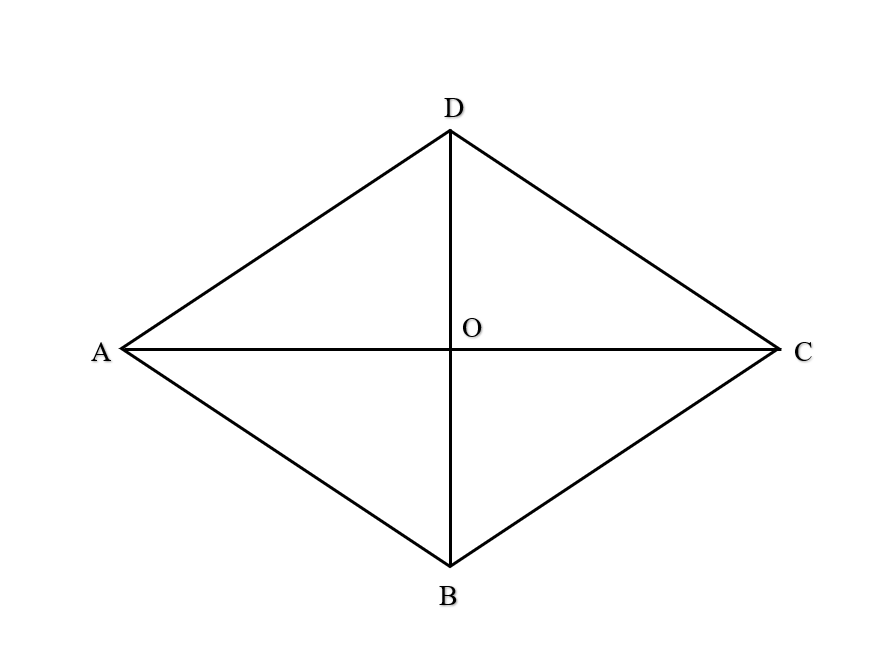
a) Ta có hình thoi ABCD có cạnh a. AO là tia phân giác của $\widehat{\text{BAD}}$ ( tính chất hình thoi ) ⇒ $\widehat{\text{DAO}}$ = 30°.

AC ⊥ BD ( tính chất hình thoi ) ⇒ $\widehat{\text{AOD}}$ = 90° ⇒ Tam giác AOD vuông tại O.

Xét tam giác AOD vuông tại O: cos$\widehat{\text{DAO}}$ =  cos30° = $\frac{\text{AO}}{\text{AD}}$ ⇒ AO = a. cos30° = $\frac{\text{a}\sqrt{3}}{2}$.

Hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường ( tính chất hình thoi )

⇒ AO = OC = $\frac{\text{a}\sqrt{3}}{2}$.

Vậy ta có hai vectơ $\overrightarrow{\text{AO}}$ và $\overrightarrow{\text{OC}}$ bằng nhau và có độ dài bằng $\frac{\text{a}\sqrt{3}}{2}$.

b) Ta có AC = AO + OC = a$\sqrt{3}$.

Vậy ta có hai vectơ $\overrightarrow{\text{AC}}$ và $\overrightarrow{\text{CA}}$ đối nhau và có độ dài a$\sqrt{3}$.

Bài 5 trang 91 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Hãy chỉ ra một cặp vectơ:

a) cùng hướng;

b) ngược hướng;

c) bằng nhau.

Lời giải:

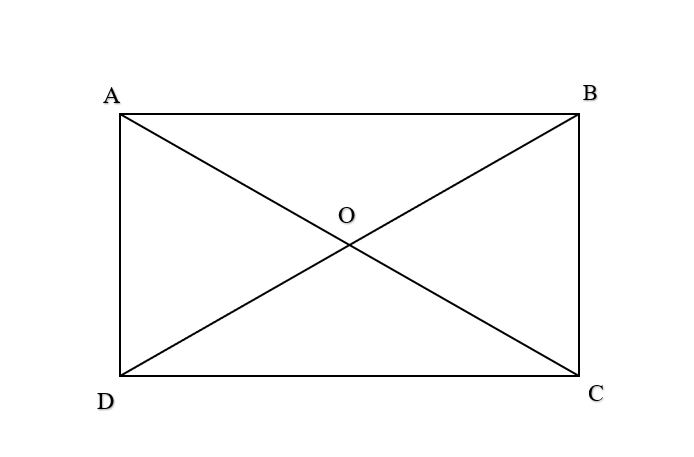
a) $\overrightarrow{\text{AO}}$ cùng hướng với $\overrightarrow{\text{AC}}$.

b) $\overrightarrow{\text{DO}}$ ngược hướng với $\overrightarrow{\text{BD}}$.

c) $\overrightarrow{\text{AB}}=\overrightarrow{\text{DC}}$ ( do có cùng hướng và AB = DC ).

Bài 6 trang 91 SBT Toán 10 Tập 1: Gọi O là tâm của hình bát giác đều ABCDEFGH.

a) Tìm hai vectơ khác $\overrightarrow{\text{0}}$ và cùng hướng với $\overrightarrow{\text{OA}}$.

b) Tìm vectơ bằng vectơ $\overrightarrow{\text{BD}}$.

Lời giải:

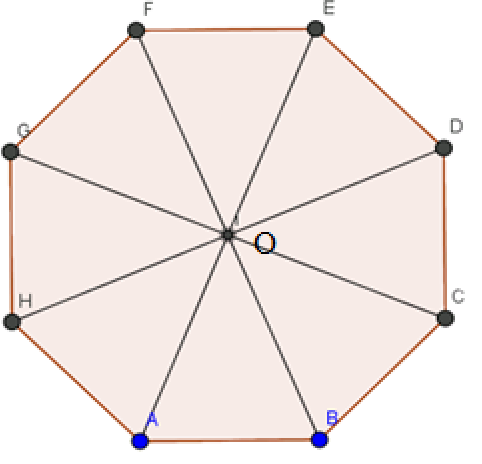
a) Hai vectơ khác $\overrightarrow{\text{0}}$ và cùng hướng với $\overrightarrow{\text{OA}}$: $\overrightarrow{\text{EO}}$, $\overrightarrow{\text{EA}}$.

b) Ta có: $\widehat{\text{DOB}}=\frac{2}{8}.360°=90°$⇒ DH vuông góc với FB.

Xét tứ giác FDBH: Hai đường chéo DH và FB vuông góc với nhau tại O là trung điểm của mỗi đường nên FDBH là hình thoi. ( DHNB hình thoi )

Lại có FB = DH ( do đều là đường chéo của bát giác đều ) nên FDBH là hình vuông. (DHNB hình vuông )

⇒ HF = BD và HF // BD.

Như vậy ta có vectơ bằng vectơ $\overrightarrow{\text{BD}}$ là $\overrightarrow{\text{HF}}$.