Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Giải bởi Vietjack
Lời giải
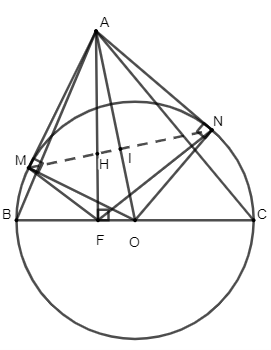
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có: \(\widehat {AMH} = \widehat {AFM}\) và \(\widehat {MAH}\) chung nên ∆AMH đồng dạng với ∆AFM
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\) ⇒ OFHI nội tiếp ⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Cho tứ diện S.ABC có đáy là tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO = 2a. Gọi I là một điểm trên OH, đặt AI = x (a < x < 2a) và (α) là mặt phẳng qua I và (α) vuông góc AH.
a) Xác định thiết diện của (α) với tứ diện S.ABC.
b) Tính diện tích thiết diện của (α) và S.ABC theo a và x.
