Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 32)
-
1915 lượt thi
-
43 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Đặt \(\sqrt {{x^2} + 5x + 28} = t{\rm{ }}\left( {t > 0} \right)\)
⇒ x2 + 5x = t2 – 28
Phương trình trở thành: t2 – 28 + 4 – 5t = 0
⇔ t2 – 5t – 24 = 0 \( \Leftrightarrow \left[ \begin{array}{l}t = 8\,\,\,\left( {tm} \right)\\t = - 3\left( {ktm} \right)\end{array} \right.\)
Với t = 8 ta có \[\sqrt {{x^2} + 5x + 28} = 8\]
⇔ x2 + 5x + 28 = 64
⇔ x2 + 5x – 36 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 9\end{array} \right.\)
Vậy \(x \in \left\{ {4; - 9} \right\}\).
Câu 2:
Cho định lí “Cho số tự nhiên n, nếu n5 chia hết cho 5 thì n chia hết cho 5”.
Định lí này được viết dưới dạng P Þ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.
 Xem đáp án
Xem đáp án
Lời giải
– Định lý đảo: Cho số tự nhiên n, nếu n chia hết cho 5 thì n5 chia hết cho 5.
– Cho số tự nhiên n, n5 chia hết cho 5 là điều kiện cần và đủ để n chia hết cho 5.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
(0,25)8 = [(0,5)2]8 = (0,5)2.8 = (0,5)16
(0,125)4 = [(0,5)3]4 = (0,5)3.4 = (0,5)12
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Gọi A là biến cố “ba viên bi lấy được chỉ có hai màu”
Ta có: Số phần tử của không gian mẫu: \(C_{16}^3 = 560\)
Số cách chọn được ba viên bi chỉ có một màu: \(C_4^3 + C_5^3 + C_7^3 = 49\)
Số cách chọn được ba viên bi có đủ ba màu: \(C_4^1 + C_5^1 + C_7^1 = 140\)
Vậy xác suất cần tìm là: \({\rm P}\left( A \right) = 1 - \frac{{49 + 140}}{{560}} = \frac{{53}}{{80}}\).
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Số cách lấy ra 8 viên bi bất kì: \(C_{16}^8 = 12\,\,870\)
Số cách lấy ra 8 viên bi không có màu vàng mà chỉ có hai màu xanh và đỏ: \(C_7^7C_5^1 + C_7^6C_5^2 + C_7^5C_5^3 + C_7^4C_5^4 + C_7^3C_5^5 = 495\)
Số cách lấy ra 8 viên bi không có màu đỏ mà có hai màu xanh và vàng:
\(C_7^7C_4^1 + C_7^6C_4^2 + C_7^5C_4^3 + C_7^4C_4^4 = 165\)
Số cách lấy ra 8 viên bi không có màu xanh mà chỉ có hai màu đỏ và vàng:
\(C_5^5C_4^3 + C_5^4C_4^4 = 9\)
Số cách lấy ra 8 viên bi có đủ 3 màu:
12 870 − (495 + 165 + 9) = 12 201 (cách).
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải.
(102 + 112 + 122) : (132 + 142)
= (10 × 10 + 11 × 11 + 12 × 12) : (132 + 142)
= [(12 + 1)2 + (12 + 2)2] : (132 + 142)
= (132 + 142) : (132 + 142)
= 1
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
y2 = x(x + 1)(x + 7)(x + 8) ⟺ y2 = (x2 + 8x)( x2 + 8x + 7)
Đặt t = x2 + 8x, ta có: y2 = t(t + 7) = t2 + 7t
⟺ 4y2 = 4t2 + 28t + 49 – 49
⟺ (2t + 7)2 – 4y2 = 49
⟺ (2t + 7 – 2y)(2t + 7 + 2y) = 49 = 7.7
\( \Leftrightarrow \left[ \begin{array}{l}2t + 7 - 2y = 7\\2t + 7 + 2y = 7\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}2{x^2} + 16x + 7 - 2y = 7\\2{x^2} + 16x + 7 + 2y = 7\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}2{x^2} + 16x - 2y = 0\\2{x^2} + 16x + 2y = 0\end{array} \right.\)
Vậy nghiệm của phương trình là: (–8; 0), (0; 0).
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
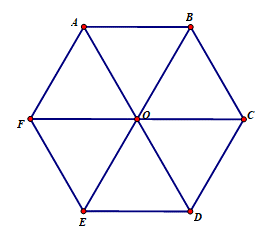
Với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau), ta có thể xếp chúng thành hình lục giác đều với các đường chéo chính cắt nhau như hình trên, ta được 6 hình tam giác đều.
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
52n+1 + 2n+4 +2n+1
= 5.52n + 24.2n + 2.2n
= 5.25n + 18.2n
= 5.25n + 23.2n – 5.2n
= 23.2n + 5(25n – 2n)
Ta có 25n – 2n ⋮ (25 – 2)
⇒ 25n – 2n ⋮ 23
⇒ 5(25n – 2n) ⋮ 23
Vì 23 ⋮ 23 ⇒ 23. 2n ⋮ 23
Vậy 23. 2n + 5(25n – 2n) ⋮ 23 ⇒ 52n+1 + 2n+4 +2n:1 ⋮ 23.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
asin2x + 2sin2x + 3acos2x = 2
⇔ 2sin2x + acos2x = 2 – 2a
Phương trình có nghiệm
⇔ 22 + a2 ≥ (2 – 2a)2
⇔ 3a2 – 8a ≤ 0 \( \Leftrightarrow 0 \le a \le \frac{8}{3}\).
Vậy đáp án đúng là: D
Câu 11:
Cho biểu thức:
\[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]
a) Rút gọn A.
b) Tìm x để A < 1.
 Xem đáp án
Xem đáp án
Lời giải
ĐKXĐ: x ≥ 0, x ≠ 25, x ≠ 9
a) \[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]
\[ = \frac{{x - 5\sqrt x - \left( {x - 25} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}:\left[ {\frac{{25 - x}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}} - \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}} + \frac{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}} \right]\]
\[ = \frac{{ - 5\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}:\frac{{25 - x - \left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right) + x - 25}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}}:\frac{{ - \left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}}.\frac{{ - \left( {\sqrt x + 5} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\]
\[ = - \frac{5}{{\sqrt x + 5}} \cdot \frac{{ - \left( {\sqrt x + 5} \right)}}{{\sqrt x + 3}}\]
\[ = \frac{5}{{\sqrt x + 3}}\].
b) Với x ≥ 0, x ≠ 25, x ≠ 9, ta có
A < 1 \[ \Leftrightarrow \frac{5}{{\sqrt x + 3}} < 1\] ⇔ \[ \Leftrightarrow \frac{{5 - \left( {\sqrt x + 3} \right)}}{{\sqrt x + 3}} < 0 \Leftrightarrow \frac{{2 - \sqrt x }}{{\sqrt x + 3}} < 0\]
\( \Leftrightarrow 2 - \sqrt x < 0\) (vì \[\sqrt x + 3 > 0\] ∀x ≥ 0, x ≠ 25, x ≠ 9)
\( \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4\)
Kết hợp điều kiện x ≥ 0, x ≠ 25, x ≠ 9 ta được: x > 4, x ≠ 25, x ≠ 9.
Vậy để A < 1 thì x > 4, x ≠ 25, x ≠ 9
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
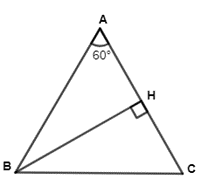
Kẻ BH ⊥ AC tại H
Xét ∆ABH vuông tại H, ta có:
\[sinA = \frac{{BH}}{{AB}}\] ⇒ BH = AB . sinA
Mặt khác \({S_{\Delta ABC}} = \frac{1}{2} \cdot BH \cdot AC = \frac{1}{2} \cdot AB \cdot AC \cdot \sin A\)
Ta có: AB + AC = 8 cm
\[ \Rightarrow 0 \le AB{\rm{ }}.{\rm{ }}AC \le {\left( {\frac{{AB + AC}}{2}} \right)^2} = 16\] (BĐT Cauchy)
\({S_{\Delta ABC}} \le \frac{1}{2} \cdot 16 \cdot \sin 60^\circ = 4\sqrt 3 \)(cm2)
Dấu bằng xảy ra khi và chỉ khi AB = AC = 4 (cm).
Vậy diện tích lớn nhất của tam giác ABC là \(4\sqrt 3 \)cm2 khi AB = AC = 4 cm.
Câu 13:
Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:
a) OM song song O'N;
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.
 Xem đáp án
Xem đáp án
Lời giải
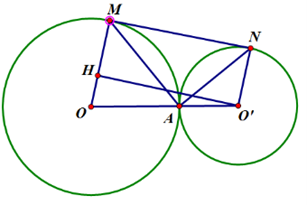
Xét ∆MAN vuông tại A có: \(\widehat {AMN} + \widehat {ANM} = 90^\circ \) (1)
Và \[\widehat {MAO} + \widehat {NAO'} = 90^\circ = 180^\circ - \widehat {MAO} = 180^\circ - 90^\circ = 90^\circ \] (2)
Lại có: ∆OMA cân tại O (OA = OM = R) ⟹ \[\widehat {OAM} = \widehat {OMA}\] (3)
∆O’NA cân tại O (O’A = O’N = R’) ⟹ \[\widehat {O'AN} = \widehat {O'NA}\](4)
Từ (1), (2), (3) và (4) suy ra:
\[\widehat {OMN} + \widehat {MNO'} = \left( {\widehat {OMA} + \widehat {AMN}} \right) + \left( {\widehat {ANM} + \widehat {O'NA}} \right)\]
\[ = \widehat {OMA} + \widehat {AMN} + \widehat {ANM} + \widehat {O'NA}\]
\[ = \widehat {OAM} + \widehat {AMN} + \widehat {ANM} + \widehat {O'AN}\]
\[ = \left( {\widehat {OAM} + \widehat {O'AN}} \right) + \left( {\widehat {AMN} + \widehat {ANM}} \right)\]
\[ = 90^\circ + 90^\circ \]
\[ = 180^\circ \]
Tứ giác OMNO’ có \[\widehat {OMN} + \widehat {MNO'} = 180^\circ \] nên MN // O’N.
b) Từ O’ kẻ O’H ⊥ OM. Khi đó:
\({S_{OMNO'}} = \frac{{\left( {O'N + OM} \right).O'H}}{2} = \frac{{\left( {R' + R} \right).O'H}}{2} \le \frac{{\left( {R' + R} \right).O'O}}{2} = \frac{{{{\left( {R' + R} \right)}^2}}}{2}\)
Dấu bằng xảy ra khi và chỉ khi O’H = O’O hay H ≡ O
⇒ O’O ⊥ MO hoặc O’O ⊥ O’N
Vậy tứ giác MNO’O có diện tích lớn nhất là \(\frac{{{{\left( {R' + R} \right)}^2}}}{2}\) khi O’O ⊥ MO hoặc O’O ⊥ O’N.
Câu 14:
Cho tứ diện S.ABC có đáy là tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO = 2a. Gọi I là một điểm trên OH, đặt AI = x (a < x < 2a) và (α) là mặt phẳng qua I và (α) vuông góc AH.
a) Xác định thiết diện của (α) với tứ diện S.ABC.
b) Tính diện tích thiết diện của (α) và S.ABC theo a và x.
 Xem đáp án
Xem đáp án
Lời giải
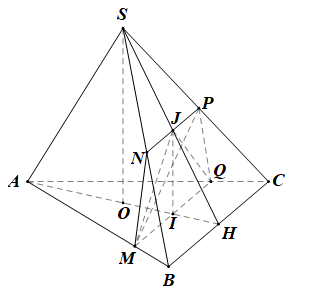
a) • Ta có: BC ⊥ OH
Qua I, dựng MQ // BC (M ∈ AB, Q ∈ AC) thì MQ ⊥ OH.
Mặt khác, ta có: SO ⊥ OH.
Dựng IJ // OS (J ∈ SH) thì IJ ∈ OH.
Do đó mp(α) là mặt phẳng (JMQ).
• Ta có: MQ // BC nên (α) // BC.
Suy ra (α) cắt (SBC) theo giao tuyến qua J và song song với BC.
Do đó, qua J dựng đường thẳng song song với BC, cắt SB và SC tại N và P ta được MNPQ là thiết diện cần dựng.
Vì NP // MQ // BC nên MNPQ là hình thang.
Ta có: OB = OC Þ DSOB = DSOC Þ SB = SC
Þ DSAB = DSAC \( \Rightarrow \widehat {SBA} = \widehat {SCA}\).
Ta cũng có: BN = CP, BM = CQ, do đó: DBMN = DCQP.
Do đó: MN = QP suy ra MP = NQ.
Vậy thiết diện là hình thang cân.
c) Do AH = 2a, ta tính được \(BC = \frac{{4a\sqrt 3 }}{3}\)
\(\frac{{MQ}}{{BC}} = \frac{{AI}}{{AH}} = \frac{x}{{2a}} \Rightarrow MQ = \frac{x}{{2a}}.\frac{{4a\sqrt 3 }}{3} = \frac{{2x\sqrt 3 }}{3}\)
\(\frac{{NP}}{{BC}} = \frac{{SJ}}{{SH}} = \frac{{OI}}{{OH}} = \frac{{x - a}}{a}\)
\( \Rightarrow NP = \frac{{x - a}}{a}.\frac{{4a\sqrt 3 }}{3} = \frac{{4\left( {x - a} \right)\sqrt 3 }}{3}\)
\(\frac{{IJ}}{{OS}} = \frac{{HI}}{{HO}} = \frac{{2a - x}}{a} \Rightarrow IJ = 2\left( {2a.x} \right)\)
\({S_{MNP}} = \frac{1}{2}\left( {MQ + NP} \right)IJ = \frac{1}{2}\left( {\frac{{2x\sqrt 3 }}{3} + \frac{{4\left( {x - a} \right)\sqrt 3 }}{3}} \right)2\left( {2a - x} \right)\)
\( = \frac{{2\sqrt 3 }}{3}\left( {3x - 2a} \right)\left( {2a - x} \right)\).
Àp dụng bất đẳng thức Cô-si:
\(\begin{array}{*{20}{r}}{}&{S = 2\sqrt 3 \left( {x - \frac{2}{3}} \right)\left( {2a - x} \right) \le 2\sqrt 3 {{\left( {\frac{{x - - a + 2a - x}}{3}} \right)}^2} = \frac{{8\sqrt 3 }}{9}{a^2}}\end{array}\)
Dấu "=" xảy ra khi \(x.\frac{2}{3}a = 2a - x \Leftrightarrow x = \frac{4}{9}a{\rm{\;}}\left( {tm} \right)\).
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
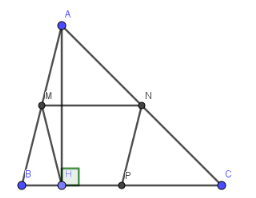
M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC ứng với cạnh BC.
⇒ MN // BC hay MN // HP ⇒ MNPH là hình thang (1)
Mặt khác: Tam giác vuông ABH có HM là đường trung tuyến ứng với cạnh huyền nên \(HM = \frac{{AB}}{2} = MB\) ⇒ ∆MHB cân tại M \[ \Rightarrow \widehat {MHB} = \widehat {MBH}\]
Mà \[\widehat {MBH} = \widehat {NPC}\] (hai góc đồng vị do NP //AB) \[ \Rightarrow \widehat {MHB} = \widehat {NPC}\]
\[ \Rightarrow {180^{\rm{o}}} - \widehat {MHB} = {180^{\rm{o}}} - \widehat {NPC}\]
Hay \[\widehat {MHP} = \widehat {NPH}\](2)
Từ (1) và (2) ⇒ MNPH là hình thang cân.
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
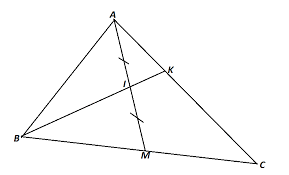
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Câu 17:
Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC.
a) Tính độ dài của MN biết AC = 16cm.
b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.
c) Trên tia đối của tia NM lấy E sao cho N là trung điểm ME. Gọi K là giao điểm của EI và MC. Chứng minh MC = 3KC.
 Xem đáp án
Xem đáp án
Lời giải
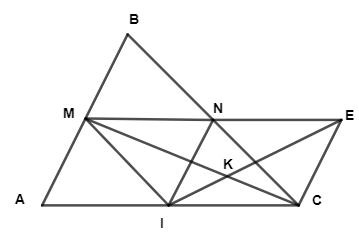
a) Xét ΔABC có: M là trung điểm của AB, N là trung điểm của BC
Do đó: MN là đường trung bình của ∆ABC
Suy ra: MN // AC và \(MN = \frac{{AC}}{2} = \frac{{16}}{2} = 8\) (cm)
b) Xét ∆ABC có M là trung điểm của AB, I là trung điểm của AC
Do đó: MI là đường trung bình của ∆ABC
Suy ra: MI // BC và \(MI = \frac{{BC}}{2}\)
Mà \(BN = \frac{{BC}}{2}\) nên MI // BN và MI = BN
Do đó tứ giác BMIN là hình bình hành
c) Ta có: \(MN = NE = \frac{{AC}}{2} = IC\)
Mà MN // IC nên NE // IC
Do đó tứ giác NECI là hình bình hành
Mà K là giao điểm của EI và MC nên \(\frac{{KC}}{{KM}} = \frac{{IC}}{{ME}} \Rightarrow \frac{{KC}}{{KM}} = \frac{1}{2}\) ⇒ KM = 2KC
Ta có: KM + KC = MC ⇔ 2KC + KC = MC ⇔ 3KC = MC
Vậy 3KC = MC
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải
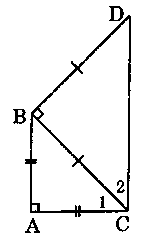
Vì ∆ABC vuông cân tại A nên \(\widehat {ABC} = \widehat {{C_1}}\)
Lại có: \(\widehat {ABC} + \widehat {{C_1}} = 90^\circ \) (tính chất tam giác vuông).
Suy ra: \[\widehat {{C_1}} = 45^\circ \]
Vì ∆BCD vuông cân tại B nên \(\widehat D = \widehat {{C_2}}\)
Lại có: \(\widehat D + \widehat {{C_2}} = 90^\circ \)(tính chất tam giác vuông).
Suy ra: \[\widehat {{C_2}} = 45^\circ \]
\(\widehat {ACD} = \widehat {{C_1}} + \widehat {{C_2}} = 45^\circ + 45^\circ = 90^\circ \)
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB // CD
Vậy tứ giác ABCD là hình thang vuông.
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
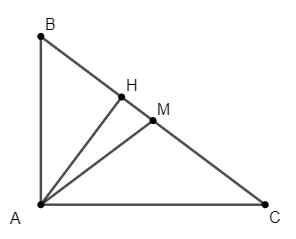
Vì ABC vuông tại A và AH là đường cao nên ta có:
AH2 = BH . HC ⇔ AH2 = 4 . 9 = 36 ⇔ AH = 6 (cm).
Vì AM là đường trung tuyến của ∆ABC nên ta có:
\[AM = \frac{1}{2}BC = \frac{1}{2}\left( {4 + 9} \right) = \frac{{13}}{2}\]
\[ \Rightarrow HM = \sqrt {A{M^2} - A{H^2}} = \sqrt {{{\left( {\frac{{13}}{2}} \right)}^2} - {6^2}} = \frac{5}{2}\]
\[ \Rightarrow {S_{AHM}} = \frac{1}{2}AH.HM = \frac{1}{2} \cdot 6 \cdot \frac{5}{2} = \frac{{15}}{2}\left( {c{m^2}} \right)\].
Câu 20:
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
 Xem đáp án
Xem đáp án
Lời giải
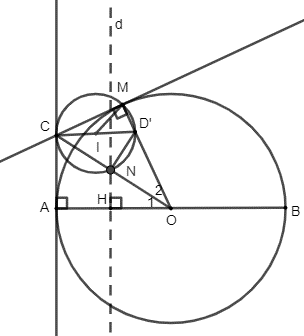
a) Do (I) tiếp xúc với AC tại C nên I ∈ đường thẳng vuông góc với AC tại C
Gọi D’ là giao của đường thẳng vuông góc với AC tại C với OM
Ta có: ∆CMD’ vuông tại M (CM nằm trên đường thẳng tiếp xúc với (O)) (1)
Lại có: (I) qua M và tiếp xúc với AC tại C tức là (I) qua M và C ⇒ IM = IC (2)
Từ (1) và (2) ⇒ I là trung điểm của CD’ (theo định lí về trung điểm và cạnh huyền của tam giác vuông)
⇒ CD’ là đường kính của (I) do ∆CMD’ vuông tại M (3)
Theo giả thiết: CD là đường kính của (I) (4)
Từ (3) và (4) ⇒ D ≡ D’ hay 3 điểm O, M, D thẳng hàng (vì D’ ∈ OM)
b) Do CA và CM là 2 tiếp tuyến của (O) cắt nhau tại C \( \Rightarrow {\widehat O_1} = {\widehat O_2}\) (theo định lí tiếp tuyến thì OC là phân giác của \(\widehat {AOM}\) (5)
Mặt khác: CD ⊥ AC và OA ⊥ AC ⇒ CD // OA \( \Rightarrow {\widehat C_1} = {\widehat O_1}\) (so le trong) (6)
Từ (5) và (6) \( \Rightarrow {\widehat C_1} = {\widehat O_2}\) ⇒ ∆CDO cân tại D
c) Do N ∈ (I) ⇒ \(\widehat {CND} = 90^\circ \) (CN ⊥ ND)
Mặt khác: N ∈ OC ⇒ N là chân đường vuông góc từ D xuống OC
Mà ∆CDO cân tại D nên DN đồng thời là đường trung tuyến ⇒ NC = NO
Gọi (d) là đường thẳng qua N và vuông góc với AB
Gọi H là giao điểm của (d) và AB ⇒ NH ⊥ AB
Xét ∆ACO và ∆HNO có \[\widehat {CAO} = \widehat {NHO} = 90^\circ \], \[{\widehat O_1}\] là góc chung
⇒ ∆ACO đồng dạng với ∆HNO (góc – góc)
⇒ \(\frac{{ON}}{{OC}} = \frac{{OH}}{{OA}} = \frac{1}{2}\) (do NO = NC)
⇒ H là trung điểm của OA (là điểm cố định do OA cố định)
Vậy khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định H.
Câu 21:
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
 Xem đáp án
Xem đáp án
Lời giải
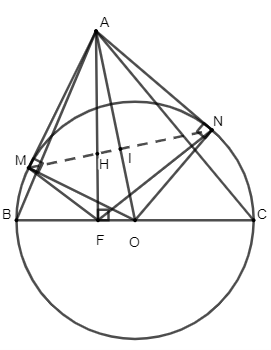
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có: \(\widehat {AMH} = \widehat {AFM}\) và \(\widehat {MAH}\) chung nên ∆AMH đồng dạng với ∆AFM
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\) ⇒ OFHI nội tiếp ⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.
Câu 22:
Cho nửa hình tròn H như hình vẽ, đường kính hình tròn là 12cm.
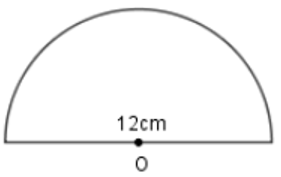
Chu vi hình H là:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Chu vi hình tròn tâm O là: 12 × 3,14 = 37,68 (cm)
Nửa chu vi của hình tròn tâm O là: 37,68 : 2 = 18,84 (cm)
Chu vi hình H là: 18,84 + 12 = 30,84 (cm)
Đáp số: 30,84 cm.
Vậy đáp án đúng là: B
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Tam giác được tạo thành bởi một trong 2 cách: lấy hai điểm trên d1 và một điểm trên d2 hoặc lấy một điểm trên d1 và hai điểm trên d2
Suy ra có \(C_{10}^2C_{15}^1 + C_{10}^1C_{15}^2\) tam giác
Vậy đáp án đúng là đáp án C.
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Sắp xếp cụm số 3,4,5 có 2 cách sắp xếp là 345 và 543
TH1: Cụm 2 số 3,4,5 đứng đầu có: 2.7.6.5 = 240 số thỏa mãn
TH2: Cụm 3 số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345
3 chữ số còn lại có: 6.6.5 = 180 cách chọn và sắp xếp
Do đó có 2.3.180 = 1080 số thỏa mãn
Theo quy tắc cộng có:
420 + 1080 = 1500 số thỏa mãn yêu cầu bài toán
Vậy đáp án đúng là đáp án D.
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
Tổng số phần bằng nhau là : 3 + 7 =10 (phần)
Giá trị 1 phần là : 60 : 10 = 6 (tấn)
Số gạo tẻ có trong kho là : 6 × 7 = 42 (tấn)
Số gạo nếp có trong kho là: 6 × 3 = 18 (tấn)
Đáp số: 42 tấn gạo tẻ, 18 tấn gạo nếp
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
Lúc đầu, số sách ở ngăn một bằng \(\frac{2}{{2 + 3}} = \frac{2}{5}\) (tổng số sách ở cả hai ngăn).
Sau khi lấy ra ở mỗi ngăn 10 quyển sách thì số sách ngăn một bằng \(\frac{3}{{5 + 3}} = \frac{3}{8}\) (tổng số sách ở cả hai ngăn).
10 quyển sách bằng \(\frac{2}{5} - \frac{3}{8} = \frac{1}{{40}}\) (tổng số sách ở cả hai ngăn).
Vậy lúc đầu tổng số sách ở cả hai ngăn là: \(10:\frac{1}{{40}} = 400\)(quyển)
Đáp số: 400 quyển.
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Một tổ có 9 học sinh được xếp thành hàng dọc.
Suy ra số phần tử của không gian mẫu là: n(Ω) = 9!
Gọi biến cố A: “5 học sinh nam đứng kề nhau”.
• Xếp 5 học sinh nam đứng kề nhau thì sẽ có 5! cách xếp.
• Sau đó ta coi 5 học sinh nam là 1 “người A”, rồi xếp “người A” cùng với 4 bạn nữ kia, tức là xếp 5 người, ta lại có 5! cách xếp.
Vì vậy n(A) = 5!.5!
Vậy xác suất của biến cố A là: \({\rm P}\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{5!.5!}}{{9!}} = \frac{5}{{126}}\)
Vậy đáp án đúng là A.
Câu 28:
 Xem đáp án
Xem đáp án
Lời giải
Để lấy 5 quân mà được 4 chất khác nhau thì có số cách lấy là:
\(C_5^1C_{13}^1.C_4^1.C_{13}^1.C_3^1.C_{13}^1.C_2^1.C_{13}^1.C_1^1.C_{12}^1\)
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải
Vì tháng 2 chỉ có 28 ngày hoặc 29 ngày mà lại có đến 5 ngày là thứ năm nên có 4 tuần kể từ thứ năm đầu đến thứ năm cuối.
Suy ra từ thứ năm đầu tiên đến thứ năm cuối cùng có số ngày là: 4 × 7 + 1 = 29 (ngày)
Như vậy 29 ngày kể từ thứ năm đầu tiên đến thứ năm cuối cùng phải trùng hoàn toàn với 29 ngày trong tháng nên ngày thứ năm đầu tiên của tháng đó là mùng 1 và ngày 29 tháng đó cũng là thứ năm.
Do đó ngày chủ nhật đầu tiên của tháng đó là ngày mùng 4. Các ngày chủ nhật của tháng đó là: 04 ; 11 ; 18 ; 25.
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng tức là không cùng nằm trên một cạnh của tam giác ABC.
Chọn ngẫu nhiên 3 điểm từ n+6 điểm đã cho có: \(C_{n + 6}^3\) (cách)
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của tam giác ABC có: \(C_4^3 + C_n^3\) (cách)
Số tam giác lập thành là:
\(C_{n + 6}^3 - \left( {C_4^3 + C_n^3} \right) = 247\)
\( \Leftrightarrow \frac{{\left( {n + 6} \right)!}}{{3!.\left( {n + 3} \right)!}} - \left[ {4 + \frac{{n!}}{{3!.\left( {n - 3} \right)!}}} \right] = 247\)
\( \Leftrightarrow \frac{{\left( {n + 6} \right)\left( {n + 5} \right)\left( {n + 4} \right)}}{6} - \left[ {4 + \frac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{6}} \right] = 247\)
⇔ (n + 6)(n + 5)(n + 4) – n(n – 1)(n – 2) = 1506
⇔ 18n2 + 72n – 1386 = 0
\( \Leftrightarrow \left[ \begin{array}{l}n = - 11\\n = 7\end{array} \right.\)
Vì n > 3 nên n = 7.
Vậy đáp án đúng là C.
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
ĐKXĐ: x ≥ 0
Ta có: \(x - 2\sqrt x + 3 = {\left( {\sqrt x - 1} \right)^2} + 2 \ge 2\)
\( \Rightarrow Q = \frac{1}{{x - 2\sqrt x + 3}} \le \frac{1}{2}\)
Dấu bằng xảy ra \( \Leftrightarrow \sqrt x - 1 = 0 \Leftrightarrow x = 1\) (thỏa mãn ĐKXĐ)
Vậy GTLN của Q là \(\frac{1}{2}\) khi x = 1.
Câu 32:
Tìm giá trị của x để đa thức dư trong mỗi phép chia sau có giá trị bằng 0:
a) (3x5 – x4 – 2x3 + x2 + 4x + 5) : (x2 – 2x + 2);
b) (x5 + 2x4 + 3x2 + x – 3) : (x2 + 1).
 Xem đáp án
Xem đáp án
Lời giải
a) (3x5 – x4 – 2x3 + x2 + 4x + 5) : (x2 – 2x + 2)
Ta đặt tính như sau:
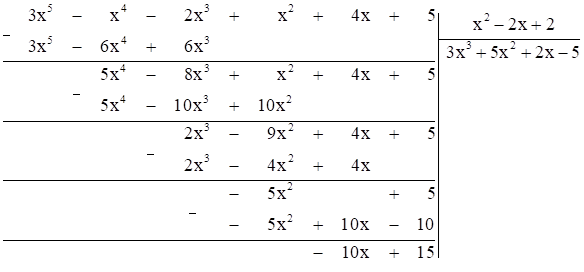
Để số dư của phép chia trên bằng 0 thì –10x + 15 = 0
\( \Leftrightarrow 10x = 15 \Leftrightarrow x = \frac{3}{2}\).
b) (x5 + 2x4 +3x2 + x – 3) : (x2 + 1)
Ta đặt tính như sau:
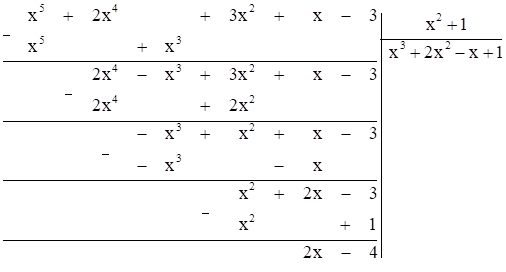
Để số dư bằng 0 thì 2x – 4 = 0 ⇔ x = 2
Câu 33:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \[{x^2}\; - 2\sqrt 3 x + 2 = 0\]
\[ \Leftrightarrow {x^2}\; - 2\sqrt 3 x + 3 - 1 = 0\]
\[ \Leftrightarrow {\left( {x - \sqrt 3 } \right)^2} = 1\]
\[ \Leftrightarrow \left[ \begin{array}{l}x - \sqrt 3 = 1\\x - \sqrt 3 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 3 \\x = - 1 + \sqrt 3 \end{array} \right.\].
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
Theo bài ta có \(\left( {xy + 1} \right)\left( {xz + 1} \right)\left( {yz + 1} \right) \vdots xyz\)
\( \Rightarrow \;\left( {{x^2}{y^2}{z^2} + {x^2}yz + x{y^2}z + xy{z^2} + xy + xz + yz + 1} \right):xyz\)
\( \Rightarrow \left( {xy + xz + yz + 1} \right){\rm{\;}} \vdots xyz\)
Đặt \(xy + xz + yz + 1 = nxyz\) \(\left( {n \in {\mathbb{N}^{\rm{*}}}} \right)\)
Do đó \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{{xyz}} = n\)
Vai trò x, y, z như nhau, không mất tính tổng quát giả sử \(x \ge y \ge z \ge 1\).
Ta có \(\frac{1}{{xyz}} \le \frac{1}{x} \le \frac{1}{y} \le \frac{1}{z} \le 1\). Vậy \(n \le 4\).
Do đó \(n \in \left\{ {1;2;3;4} \right\}\)
Trường hợp 1: Xét \(n = 1\). Ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{{xyz}} = 1\)
Ta có \(1 = \frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{{xyz}} \le \frac{4}{z} \Rightarrow z \le 4\)
Mà z > 1. Vậy \(z \in \left\{ {2;3;4} \right\}\)
• Với z = 2 ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{2} + \frac{1}{{2xy}} = 1 \Leftrightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{{2xy}} = \frac{1}{2}\)
\( \Rightarrow \frac{1}{2} = \frac{1}{x} + \frac{1}{y} + \frac{1}{{2xy}} < \frac{3}{y} \Rightarrow y < 6\)
Mà y > 1 nên \(y \in \left\{ {2;3;4;5} \right\}\).
Xét \(y \in \left\{ {2;3;4;5} \right\}\) được y = 3; x = 7.
• Với z = 3 ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{3xy}} = \frac{2}{3}\)
\( \Rightarrow \frac{2}{3} = \frac{1}{x} + \frac{1}{y} + \frac{1}{{3xy}} < \frac{3}{y} \Rightarrow y \le 4\)
Mà \(y \ge z = 3\) nên \(y \in \left\{ {3;4} \right\}\)
Xét \({\rm{y}} \in \left\{ {3;4} \right\}\), ta có \({\rm{x}} \notin \mathbb{Z}\).
• Với z = 4 ta có \(\frac{1}{{\rm{x}}} + \frac{1}{{\rm{y}}} + \frac{1}{{4{\rm{xy}}}} = \frac{3}{4}\)
\( \Rightarrow \frac{3}{4} = \frac{1}{x} + \frac{1}{y} + \frac{1}{{4xy}} < \frac{3}{4} \Rightarrow y < 4\)
Trái với \({\rm{y}} \ge {\rm{z}} = 4\).
Trường hợp 2: Xét n = 2 ta có \(\frac{1}{{\rm{x}}} + \frac{1}{{\rm{y}}} + \frac{1}{{\rm{z}}} + \frac{1}{{{\rm{xyz}}}} = 2\)
Ta có \(2 = \frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{{xyz}} \le \frac{4}{z} \Rightarrow {\rm{z}} \le 2 \Rightarrow {\rm{z}} \in \left\{ {1;2} \right\}\)
• Với z = 1, ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{xy}} = 1\)
\( \Leftrightarrow 1 = \frac{1}{x} + \frac{1}{y} + \frac{1}{{xy}} \le \frac{3}{y} \Rightarrow y \le 3\) mà \(y \in \left\{ {2;3} \right\}\)
+) y = 2 thì x = 3;
+) y = 3 thì \(x \notin Z\)
• Với z = 2, ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{2xy}} = \frac{3}{2}\)
\( \Rightarrow \frac{3}{2} = \frac{1}{x} + \frac{1}{y} + \frac{1}{{2xy}} < \frac{3}{y} \Rightarrow y < 2\)
Trái với \({\rm{y}} \ge {\rm{z}} = 2\)
Trường hợp 3: Xét n = 3, ta có \(\frac{1}{{\rm{x}}} + \frac{1}{{\rm{y}}} + \frac{1}{{\rm{z}}} + \frac{1}{{{\rm{xyz}}}} = 3\)
\( \Rightarrow 3 = \frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{{xyz}} \le \frac{4}{z} \Rightarrow z \le 1 \Rightarrow z = 1\)
Với z = 1, ta có \(\frac{1}{x} + \frac{1}{y} + \frac{1}{{xy}} = 2\)
\( \Rightarrow 2 = \frac{1}{x} + \frac{1}{y} + \frac{1}{{xy}} \le \frac{3}{y} \Rightarrow y \le \frac{3}{2} \Rightarrow y = 1\).
Khi đó x = 2.
Trường hợp 4: Xét n = 4, ta có \(\frac{1}{{\rm{x}}} + \frac{1}{{\rm{y}}} + \frac{1}{{\rm{z}}} \le \frac{1}{{{\rm{xyz}}}} = 4\)
Dấu '=' xảy ra có x = y = z = 1.
Kết luận: Các bộ số nguyên dương (x, y, z) cần tìm là (7; 3; 2); (3; 2; 1); (2; 1; 1); (1; 1; 1) và các hoán vị.
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải
Ta thực hiện đặt tính như sau:
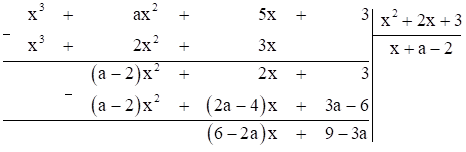
Để phép chia là phép chia hết thì số dư bằng 0
\( \Leftrightarrow \left\{ \begin{array}{l}6 - 2a = 0\\9 - 3a = 0\end{array} \right. \Leftrightarrow a = 3\).
Câu 36:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\)
\( = \frac{{{{\left( {{x^3}} \right)}^2} - {{\left( {{y^3}} \right)}^2}}}{{{x^3}\left( {x - y} \right) + {y^3}\left( {x - y} \right)}}\)
\( = \frac{{\left( {{x^3} + {y^3}} \right)\left( {{x^3} - {y^3}} \right)}}{{\left( {{x^3} + {y^3}} \right)\left( {x - y} \right)}}\)
\( = \frac{{{x^3} - {y^3}}}{{x - y}}\)
\( = \frac{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}}{{x - y}}\)
\( = {x^2} + xy + {y^2}\).
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
Các tia có gốc là O và đi qua một trong 3 điểm A, B, C là: OA, OB, OC.
Vậy có 3 tia thỏa mãn yêu cầu.
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có:
\[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {A{B^2} + A{D^2}} = 5\]
⇒ \[\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = \;AC = 5\]
Vậy đáp án đúng là B
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
12 người làm xong công việc trong 10 ngày
Vậy 1 người 10 ngày làm đc: \(\frac{1}{{12}}\) (công việc)
⇒ 1 người 1 ngày làm đc: \(\frac{1}{{120}}\) (công việc)
⇒ 1 người 8 ngày làm đc: \(8 \cdot \frac{1}{{120}} = \frac{8}{{120}} = \frac{1}{{15}}\) (công việc)
Vâỵ muốn làm xong công việc đó trong 8 ngày thì cần số người là:
\(1:\frac{1}{{15}} = 15\) (người).
Đáp số: 15 người
Câu 40:
 Xem đáp án
Xem đáp án
Lời giải
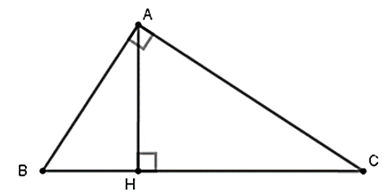
Ta có: BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.HC = 9.25 = 225
⇒ AB = 15 (cm)
AC2 = CH.BC = 16.25 = 400
⇒ AC = 20 (cm)
Lại có: AH.BC = AB.AC \( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{15.20}}{{25}} = 12\) (cm)
Vậy AB = 15 cm, AC = 20 cm, AH = 12 cm
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(\left( {x + \sqrt {{x^2} + \sqrt {2005} } } \right)\left( {\sqrt {{x^2} + \sqrt {2005} } - x} \right) = {x^2} + \sqrt {2005} - {x^2} = \sqrt {2005} \)
Mà theo bài cho ta có:
\(\left( {x + \sqrt {{x^2} + 2005} } \right)\left( {y + \sqrt {{y^2} + \sqrt {2005} } } \right) = \sqrt {2005} \)
\( \Leftrightarrow \left( {x + \sqrt {{x^2} + 2005} } \right)\left( {y + \sqrt {{y^2} + \sqrt {2005} } } \right) = \left( {x + \sqrt {{x^2} + \sqrt {2005} } } \right)\left( {\sqrt {{x^2} + \sqrt {2005} } - x} \right)\)
\( \Leftrightarrow y + \sqrt {{y^2} + \sqrt {2005} } = \sqrt {{x^2} + 2005} - x\) (1)
Chứng minh tương tự ta có: \(x + \sqrt {{x^2} + 2005} = \sqrt {{y^2} + \sqrt {2005} } - y\) (2)
Cộng từng vế của (1) và (2), ta có:
\(x + \sqrt {{x^2} + \sqrt {2005} } + y + \sqrt {{y^2} + \sqrt {2005} } = \sqrt {{x^2} + \sqrt {2005} } - x + \sqrt {{y^2} + \sqrt {2005} } - y\)
\( \Leftrightarrow x + y = - x - y\)
\( \Leftrightarrow x + y = 0\).
Vậy x + y = 0.
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(cot{\rm{ }}a = \frac{1}{{\tan a}};\,\,\,cot{\rm{ }}b = \frac{1}{{\tan b}}\)
\( \Rightarrow cot{\rm{ }}a--cot{\rm{ }}b{\rm{ }} = \frac{1}{{\tan a}} - \frac{1}{{\tan b}}\) (đpcm)
Câu 43:
 Xem đáp án
Xem đáp án
Lời giải
Với m = 0 hàm số không xác định
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{\sqrt {{m^2}{x^2} + m - 1} }} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 + \frac{1}{x}}}{{ - \sqrt {{m^2} + \frac{{m - 1}}{{{x^2}}}} }} = \frac{{ - 1}}{{\left| m \right|}}\)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{\sqrt {{m^2}{x^2} + m - 1} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \frac{1}{x}}}{{\sqrt {{m^2} - \frac{{m - 1}}{{{x^2}}}} }} = \frac{1}{{\left| m \right|}}\)
Suy ra đồ thị hàm số luôn có 2 tiệm cận ngang
Để đồ thị hàm số có 4 tiệm cận thì cần có thêm 2 tiệm cận đứng
⇒ m2x2 + m – 1 = 0 có 2 nghiệm phân biệt
\( \Rightarrow {x^2} = \frac{{1 - m}}{{{m^2}}}\)
Do x2 > 0 ⇒ 1 – m > 0 ⇒ m < 1
Vậy \(\left\{ \begin{array}{l}m < 1\\m \ne 0\end{array} \right.\) thì đồ thị hàm số có 4 tiệm cận.
