Cho hình vuông ABCD có cạnh bằng a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. M là giao điểm của CE và DF.

a) Chứng minh tứ giác EFGH là hình vuông.

b) Chứng minh DF ^ CE và ∆MAD cân.

c) Tính diện tích tam giác MDC theo a.

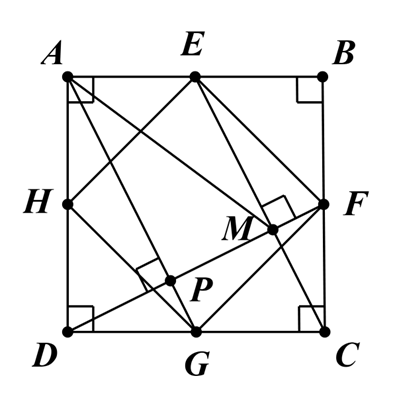
a) Xét ∆AEH và ∆BEF, có:

AE = BE (E là trung điểm AB);

AH = BF (do \(AH = \frac{1}{2}AD,\;BF = \frac{1}{2}BC\) và AD = BC);

\(\widehat {HAE} = \widehat {EBF} = 90^\circ \)

Do đó ∆AEH = ∆BEF (c.g.c).

Suy ra HE = EF (cặp cạnh tương ứng).

Chứng minh tương tự, ta được EF = GF và GH = GF.

Do đó tứ giác EFGH là hình thoi (1)

Ta có BE = BF (do \(BE = \frac{1}{2}AB,\;BF = \frac{1}{2}BC\) và AB = BC)

và \(\widehat {EBF} = 90^\circ \) (do ABCD là hình vuông).

Suy ra ∆BEF vuông cân tại B.

Do đó \(\widehat {BEF} = 45^\circ \)

Chứng minh tương tự, ta được \(\widehat {AEH} = 45^\circ \)

Ta có \(\widehat {AEH} + \widehat {HEF} + \widehat {FEB} = 180^\circ \) (kề bù).

\( \Leftrightarrow \widehat {HEF} = 180^\circ - \widehat {AEH} - \widehat {FEB} = 180^\circ - 45^\circ - 45^\circ = 90^\circ \;\left( 2 \right)\)

Từ (1), (2), suy ra tứ giác EFGH là hình vuông.

b) Xét ∆CBE và ∆DCF, có:

CB = DC (ABCD là hình vuông);

\(\widehat {CBE} = \widehat {DCF} = 90^\circ \)

BE = CF (do \(BE = \frac{1}{2}AB,\;CF = \frac{1}{2}BC\) và AB = BC).

Do đó ∆CBE = ∆DCF (c.g.c).

Suy ra \(\widehat {ECB} = \widehat {FDC}\) (cặp góc tương ứng).

Mà \(\widehat {DFC} + \widehat {FDC} = 90^\circ \) (∆DFC vuông tại C).

Do đó \(\widehat {DFC} + \widehat {ECB} = 90^\circ \)

Tam giác CFM, có: \(\widehat {CMF} = 180^\circ - \left( {\widehat {DFC} + \widehat {ECB}} \right) = 90^\circ \)

Vậy DF ^ CE tại M.

Gọi P là giao điểm của AG và DF.

Chứng minh tương tự như trên, ta được AG ^ DF tại P.

Mà CE ^ DF (chứng minh trên).

Suy ra CE // AG.

∆DMC có: G là trung điểm của DC (giả thiết) và PG // MC (chứng minh trên).

Suy ra GP là đường trung bình của ∆DMC.

Do đó P là trung điểm DM.

∆AMD có: AP vừa là đường trung tuyến, vừa là đường cao.

Vậy ∆AMD cân tại A.

c) Xét ∆DMC và ∆DCF, có:

\(\widehat {MDC}\) chung;

\(\widehat {DMC} = \widehat {DCF} = 90^\circ \)

Do đó ∆DMC ᔕ ∆DCF (g.g).

Suy ra \(\frac{{DM}}{{DC}} = \frac{{MC}}{{CF}} = \frac{{DC}}{{DF}}\) (*)

Ta có \({S_{DMC}} = \frac{1}{2}MC\,.\,MD\) và \({S_{DCF}} = \frac{1}{2}DC\,.\,CF\)

Suy ra \(\frac{{{S_{DMC}}}}{{{S_{DCF}}}} = \frac{{MC\,.\,MD}}{{DC\,.\,CF}} = \frac{{D{M^2}}}{{D{C^2}}}\)

Do đó \({S_{DMC}} = \frac{{D{M^2}}}{{D{C^2}}}.\,{S_{DCF}} = \frac{{D{M^2}}}{{D{C^2}}}.\,\frac{1}{2}CD\,.\,CF = \frac{{D{M^2}}}{{{a^2}}}\,.\,\frac{1}{2}a\,.\,\frac{a}{2} = \frac{{D{M^2}}}{4}\)

Tam giác CDF vuông tại C:

\(DF = \sqrt {D{C^2} + C{F^2}} = \sqrt {D{C^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\)

Từ (*), ta có: DM.DF = DC².

\( \Leftrightarrow DM\,.\,\frac{{a\sqrt 5 }}{2} = {a^2}\)

\( \Rightarrow DM\, = \frac{{2a\sqrt 5 }}{5}\)

Vậy \({S_{DMC}} = \frac{{D{M^2}}}{4} = {\left( {\frac{{2a\sqrt 5 }}{5}} \right)^2}\,.\,\frac{1}{4} = \frac{{{a^2}}}{5}\).