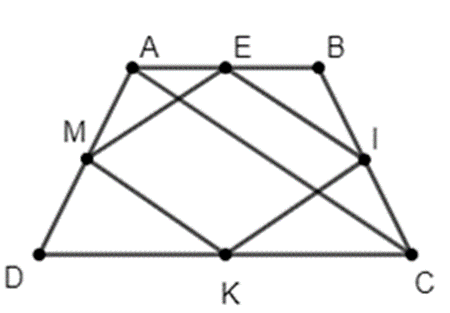
a) Xét ∆AED và ∆BEC có:

AE = BE

\(\widehat {EAD} = \widehat {EBC}\) (Vì ABCD là hình thang cân)

AD = BC (Vì ABCD là hình thang cân)

Do đó ∆AED = ∆BEC (c.g.c)

Þ ED = EC (Hai cạnh tương ứng bằng nhau)

Xét ∆EDC có DE = EC (cmt)

Do đó ∆EDC cân tại E

b) Xét ∆ADC có:

AM = MD (gt)

DK = KC (gt)

Do đó MK là đường trung bình của ∆ADC

Þ MK // AC và \(MK = \frac{1}{2}AC\) (1)

Chứng minh tương tự, ta có: EI là đường trung bình của ∆ABC

Þ EI // AC và \(EI = \frac{1}{2}AC\) (2)

Từ (1) và (2) suy ra: MK // EI và MK = EI

Do đó EIKM là hình bình hành (3)

Lại có: ME là đường trung bình của ∆ABD

\( \Rightarrow ME = \frac{1}{2}BD\)

Mà BD = AC (Vì ABCD là hình thang cân)

nên ME = MK (4)

Từ (3) và (4) suy ra: EIKM là hình thoi

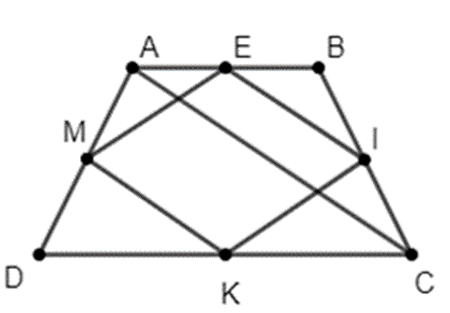
a) Xét tam giác ABC có E; I lần lượt là trung điểm của AB và BC.

Suy ra ta có EI là đường trung bình của tam giác ABC.

Do đó EI // AC, \(EI = \frac{1}{2}AC\) (1)

Chứng minh tương tự ta có: MK // AC, \(MK = \frac{1}{2}AC\) (2)

ME // BD, \(ME = \frac{1}{2}BD\) (3)

Mặt khác AC = BD (do tứ giác ABCD là hình thang cân) (4)

Từ (3) và (4) suy ra \[ME = \frac{1}{2}AC = MK\] (5)

Từ (1); (2); (5) suy ra tứ giác EIKM là hình thoi.

b) Để tứ giác EIMK là hình vuông thì EM ^ EI.

Mà theo câu a) ta có: EI // AC; EM // BD.

Khi đó suy ra để tứ giác EIMK là hình vuông thì AC ^ BD.

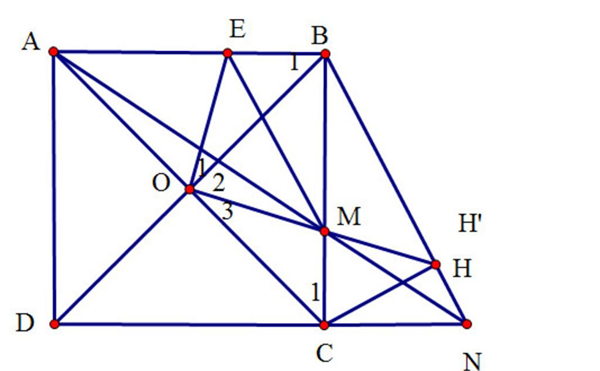
a) Xét ∆OEB và ∆OMC

Vi ABCD là hình vuông nên ta có: OB = OC

Và \[\widehat B = \widehat C = 45^\circ \]

BE = CM (gt)

Þ ∆OEB = ∆OMC (c.g.c)

Þ OE = OM và \({\widehat O_1} = {\widehat O_3}\)

Lại có: \({\widehat O_1} + {\widehat O_2} = \widehat {BOC} = 90^\circ \) vì tứ giác ABCD là hình vuông

\({\widehat O_1} + {\widehat O_2} = \widehat {EOM} = 90^\circ \) kết hợp với OE = OM

Þ ∆OEM vuông cân tại O.

b) Tứ giác ABCD là hình vuông Þ AB = CD và AB // CD

AB // CD Þ AB // CN \( \Rightarrow \frac{{AM}}{{MN}} = \frac{{BM}}{{MC}}\) (Theo định lý Ta-lét) (*)

Mà BE = CM (gt) và AB = CD Þ AE = BM thay vào (*)

Ta có: \[\frac{{AM}}{{MN}} = \frac{{AE}}{{EB}} \Rightarrow ME\;{\rm{//}}\;BN\] (theo định lý đảo Ta-lét)

c) Gọi H¢ là giao điểm của OM và BN

Từ ME // BN \[ \Rightarrow \widehat {OME} = \widehat {OH'E}\] (Cặp góc ở vị trí so le trong)

Mà \[\widehat {OME} = 45^\circ \] vì ∆OME vuông cân tại O

\( \Rightarrow \widehat {MH'B} = 45^\circ = \widehat {{C_1}}\)

Þ ∆OMC = ∆BMH¢ (g.g)

\( \Rightarrow \frac{{OM}}{{OB}} = \frac{{MH'}}{{MC}}\), kết hợp \( \Rightarrow \widehat {OMB} = \widehat {CMH'}\) (hai góc đối đỉnh)

Þ ∆OMB = ∆CMH¢ (c.g.c) \( \Rightarrow \widehat {OBM} = \widehat {MH'C} = 45^\circ \)

Vậy \(\widehat {BH'C} + \widehat {BH'M} + \widehat {MH'C} = 90^\circ \Rightarrow CH' \bot BN\)

Mà CH ^ BN (H Î BN) Þ H = H¢ hay 3 điểm O, M, H thẳng hàng (đpcm).

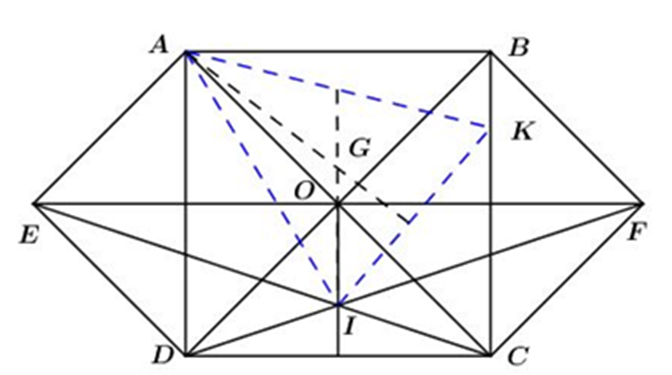
a) Gọi giao điểm của AD và EO là T

Giao điểm của BC và OF là H

Xét tứ giác EAOD có

\(\left. \begin{array}{l}AT = TD\\ET = TO\end{array} \right\} \Rightarrow EAOD\) là hình bình hành (dấu hiệu nhận biết).

Mà AD ^ EO nên tứ giác EAOD là hình thoi.

Hình thoi EAOD có \[\widehat {AOD} = 90^\circ \] nên là hình vuông.

Vậy EAOD là hình vuông theo dấu hiệu nhận biết hình thoi có 1 góc vuông.

Chứng minh tương tự với tứ giác OBFC.

b) Xét 2 tam giác ECF và FDE có:

\(\widehat {CFE} = \widehat {DEF} = 45^\circ \)

EF chung

FC = DE

Þ ΔECF = ∆FDE (c.g.c)

\( \Rightarrow \widehat {FEC} = \widehat {EFD}\)

Vậy tam giác EFI cân.

Mà O là trung điểm của EF Þ OI ^ EF (trong tam giác cân đường trung tuyến cũng là đường cao)

c) Ta có: ΔAED = ∆ABO = ∆BCO = ∆COD = ∆DOA = ∆BFC

S_AED + S_ABO + S_BCO + S_COD + S_DOA + S_BFC = S_ABFCDE = 6

Þ S_ABO = S_BCO = S_COD = S_DOA = 1

Þ S_ABCD = S_ABO + S_BCO + S_COD + S_DOA = 4

\( \Rightarrow AB = BC = CD = AD = \sqrt 4 = 2\)

d) Gọi M là giao điểm của IO với AB, N là giao điểm của IM với AK, ta có:

IO ^ FE Þ IO ^ AB Þ OM ^ AB, mà O là trung điểm của của HT nên M là trung điểm của AB.

Xét tam giác ABK có:

MA = MB (cmt)

MN // BK (vì MO // CD)

Do đó NA = NK

Þ N là trung điểm của AK

Þ IN là đường trung tuyến của ∆AIK.

Mà G là trọng tậm tam giác nên G Î IN

Þ G Î M với IM cố định (I, M cố định).

Vậy điểm G luôn nằm trên đường thẳng cố định IM.

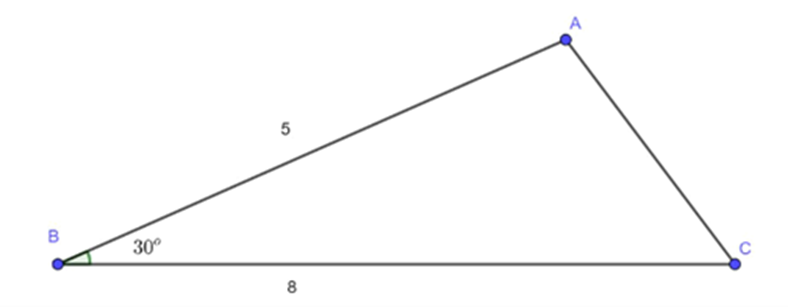
Diện tích tam giác ABC là:

\({S_{\Delta ABC}} = \frac{1}{2}AB\,.\,BC\,.\,\sin \widehat {ABC} = \frac{1}{2}\,.\,5\,.\,8\,.\,\sin 30^\circ = 10\;\left( {c{m^2}} \right)\)

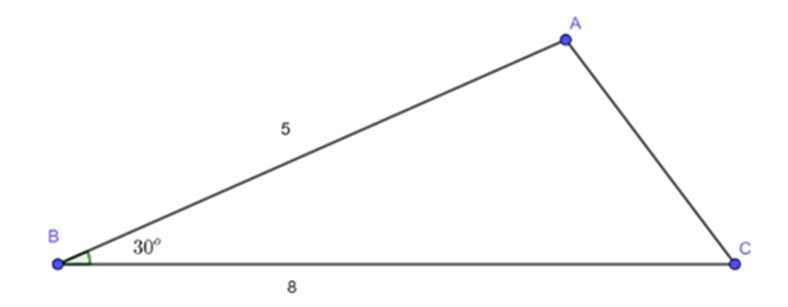
Ta có:

\[\overrightarrow {BA} \,.\,\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|\,.\,\left| {\overrightarrow {BC} } \right|\,.\,\cos \left( {\overrightarrow {BA} \,,\,\overrightarrow {BC} } \right) = 5\,.\,8\,.\,\cos 30^\circ = 20\sqrt 3 \;\left( {c{m^2}} \right)\]

Vậy \(\overrightarrow {BA} \,.\,\overrightarrow {BC} = 20\sqrt 3 \)

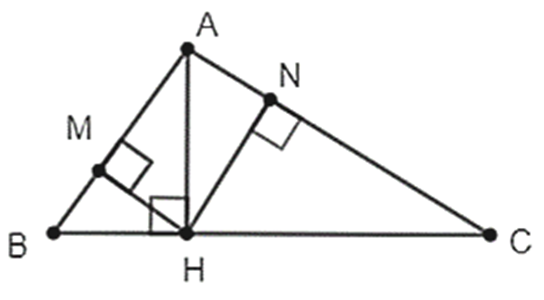
Xét ∆AHB vuông tại H có đường cao MH nên ta có: MH² = MB.MA.

Do đó \(MH = \sqrt {8\,.\,2} = 4\;\left( {cm} \right)\).

Áp dụng định lý Py−ta−go vào ∆AMH vuông tại M, ta có:

\[AH = \sqrt {A{M^2} + M{H^2}} = \sqrt {{8^2} + {4^2}} = 4\sqrt 5 \;\left( {cm} \right)\]

Vậy \(AH = 4\sqrt 5 \,\,cm;\;MH = 4\,\,cm.\)

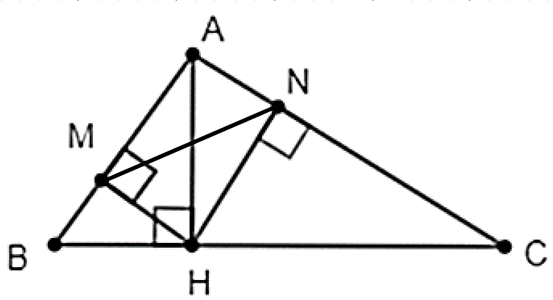
a) Áp dụng hệ thức lượng trong tam giác vuông:

AM.AB = AH²

AN.AC = AH²

Þ AM.AB = AN.AC (đpcm)

b) Vì \(AM\,.\,AB = AN\,.\,AC \Rightarrow \frac{{AM}}{{AN}} = \frac{{AC}}{{AB}}\)

Xét ∆AMN và ∆ACB có:

\[\widehat A\] chung

\(\frac{{AM}}{{AN}} = \frac{{AC}}{{AB}}\) (cmt)

Do đó ∆AMN ᔕ ∆ACB (c.g.c)

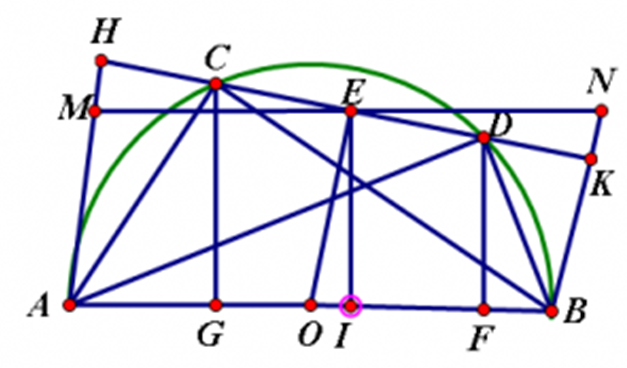
a) Gọi O là tâm đường tròn đường kính AB 

Kẻ OE vuông góc với CD (E thuộc CD)

Suy ra E là trung điểm của CD 

Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song với cạnh đáy)

Þ EH = EK mà EC = ED

Suy ra CH = DK (đpcm)

b) Hạ CG, DF ^ AB tại G, F

Þ CG // DF

Þ Tứ giác CDGF là hình thang.

Lấy I là trung điểm của GF.

 Xét hình thang CDGF có:

EC = ED (E là trung điểm của CD)

IG = IF (I là trung điểm của GF)

Þ EI là đường trung bình của hình thang CDFG

\( \Rightarrow EI = \frac{{DF + CG}}{2}\)

Ta có: \[{S_{ACB}} + {S_{ADB}} = \frac{{AB + CG}}{2} + \frac{{AB + DF}}{2} = AB\,.\,\frac{{CG + DF}}{2} = AB\,.\,EI\] (1)

Qua E kẻ đường thẳng song song với AB cắt AH, BK lần lượt ở M, N.

Dễ thấy tứ giác AMNB là hình bình hành (vì có 2 cặp cạnh đối song song )

Þ S_AMNB = AB.EI

Xét ∆MHE và ∆NKE có:

\(\widehat {MEH} = \widehat {NEK}\) (2 góc đối đỉnh)

\(\widehat {MHE} = \widehat {NKE} = 90^\circ \)

EM = EN

Do đó ∆HEM = ∆KEN (cạnh huyền – góc nhọn)

Þ S_HEM = S_KEN

Khi đó: 

S_AHKB = S_AMEKB + S_MHE = S_AMEKB + S_ENK = S_AMNB = AB.EI (2)

Từ (1) và (2) Þ S_AHKB = S_ACB + S_ADB

c) \({S_{AHKB}} = \frac{{\left( {AH + BK} \right)\,.\,HK}}{2} = \frac{{2OE\,.\,HK}}{2} = OE\,.\,HK\)

\(OE = \sqrt {O{D^2} - E{D^2}} = \sqrt {{{15}^2} - {9^2}} = 12\)

Þ S = 12.HK ≤ 12.AB = 12.30 = 360

Þ S_max = 360.

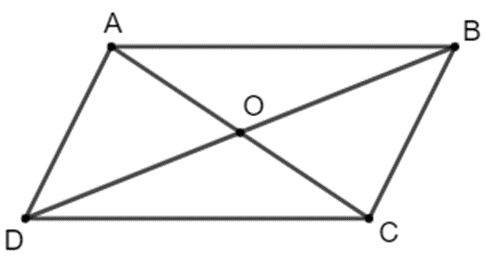
+ Do ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)

Do đó: \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\). Vậy khẳng định a) đúng.

+ Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AD} } \right|\)

Mà \(\overrightarrow {AD} = \overrightarrow {BC} \) (do AD // = BC)

Do đó: \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} = - \overrightarrow {CB} \)

Vậy khẳng định b) sai.

+ Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC và BD.

Khi đó ta có: \(\overrightarrow {OA} = \overrightarrow {CO} ;\;\overrightarrow {OD} = \overrightarrow {BO} \)

Do đó: \(\left\{ \begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {CB} = - \overrightarrow {BC} \\\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OC} + \overrightarrow {BO} = \overrightarrow {BO} + \overrightarrow {OC} = - \overrightarrow {BC} \end{array} \right.\)

Suy ra: \(\overrightarrow {OA} + \overrightarrow {OB} = - \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right)\)

Vậy khẳng định c) sai.

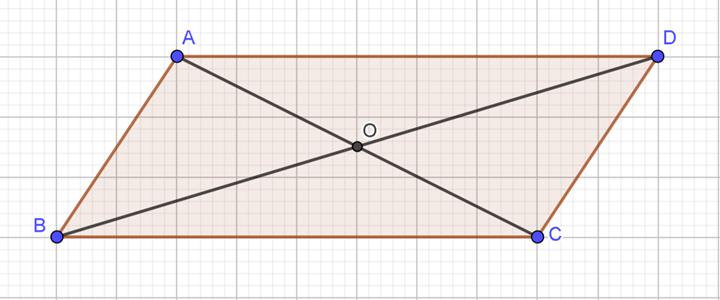
Quan sát hình vẽ ta thấy: \(\overrightarrow {AB} = \overrightarrow {DC} ;\) \[\overrightarrow {OB} = \overrightarrow {DO} ;\] \(\overrightarrow {CB} = \overrightarrow {DA} .\)

Do đó, đáp án C là sai

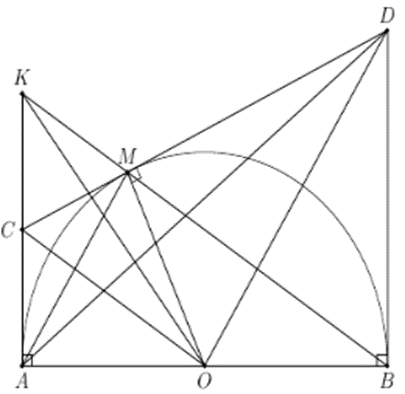
Ta có: S_CAM + S_MBD = S_CABD − S_AMB nhỏ nhất khi S_CABD nhỏ nhất và S_AMB lớn nhất

Ta thấy S_AMB lớn nhất khi M là điểm chính giữa (dễ dàng chứng minh)
Mặt khác: \({S_{CABD}} = \frac{{\left( {CA + BD} \right)\,.\,AB}}{2} = \left( {CA + BD} \right)\,.\,R\)

\( \ge 2\sqrt {CA\,.\,BD} \,.\,R = 2\sqrt {OA\,.\,OD} \,.\,R = 2{R^2}\)

Vậy để S_CABD nhỏ nhất thì CA = BD khi đó M cũng là điểm chính giữa nửa đường tròn.

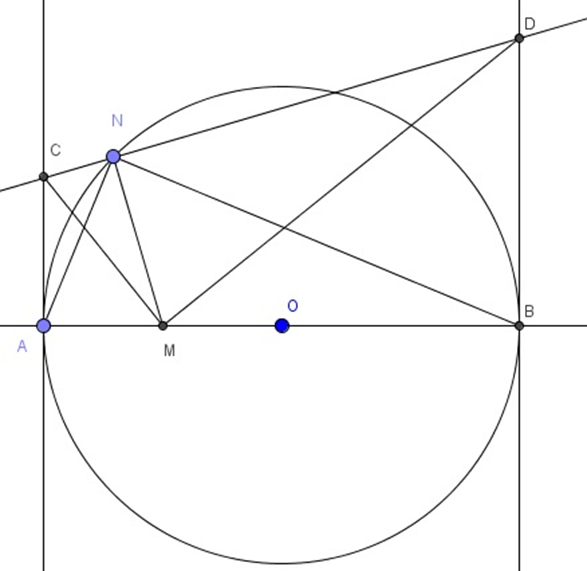
Tứ giác AMNC có \(\widehat {MAC} + \widehat {MNC} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác AMNC là tứ giác nội tiếp đường tròn

Khi đó \(\widehat {CNM} = \widehat {CMA}\) (Hai góc cùng chắn cung CA)

Chứng minh tương tự ta được MBDN là tứ giác nội tiếp nên suy ra

\(\widehat {DNB} = \widehat {DMB}\) (Hai góc cùng chắn cung DB)

Suy ra \(\widehat {CNM} + \widehat {DNB} = \widehat {CMA} + \widehat {DMB}\)

\( \Rightarrow 180^\circ - \left( {\widehat {CNM} + \widehat {DNB}} \right) = 180^\circ - \left( {\widehat {CMA} + \widehat {DMB}} \right)\)

\( \Rightarrow \widehat {ANB} = \widehat {CMD} \Rightarrow \widehat {CMD} = 90^\circ \Rightarrow CM \bot DM\)

Suy ra \[\widehat {CMA} + \widehat {DMB} = 90^\circ \]

Mà \[\widehat {CMA} + \widehat {ACM} = 90^\circ \]

Do đó \(\widehat {ACM} = \widehat {BMD}\)

Xét ∆ACM và ∆BMD có:

\(\widehat {ACM} = \widehat {BMD}\) (cmt)

\(\widehat {CAM} = \widehat {MBD} = 90^\circ \)

Suy ra ∆ACM ᔕ ∆BMD (g.g)

\( \Rightarrow \frac{{AM}}{{BD}} = \frac{{AC}}{{BM}} \Rightarrow AM\,.\,BM = BD\,.\,AC\) (không đổi)

Theo Bunhiacopxki, ta có:

(AM.BM + AC.BD)² ≤ (AM² + AC²)(BM² + BD²) = MC².MD² = 4(S_DMC)²

Þ S_DMC đạt giá trị nhỏ nhất khi AC = AM, BD = BM

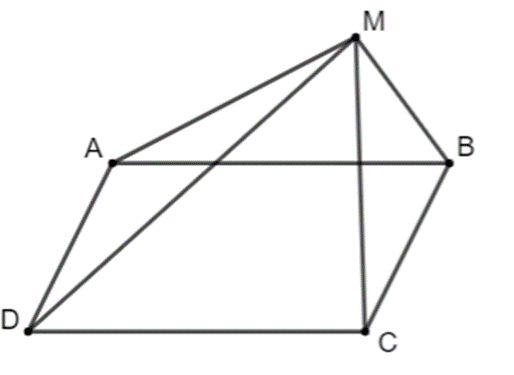
Ta có: \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {AB} & (1)\)

\(\overrightarrow {MC} - \overrightarrow {MD} = \overrightarrow {DC} & (2)\)

Do ABCD là hình bình hành nên AB // DC và AB = DC do đó: \[\overrightarrow {AB} = \overrightarrow {DC} \; & (3)\]

Từ (1), (2), (3) suy ra \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \)

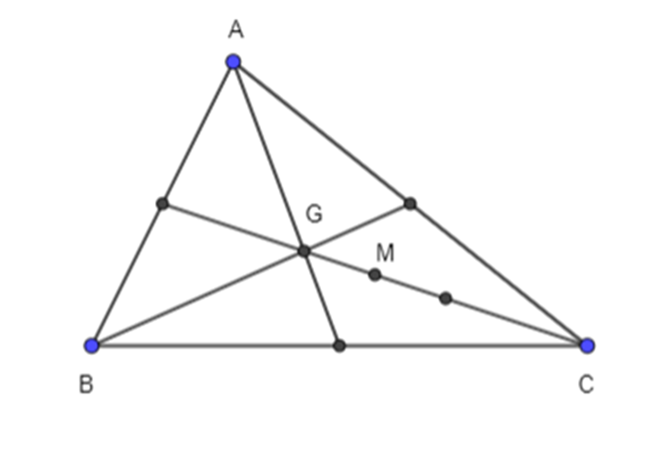
a) Gọi G là trọng tâm tam giác ABC, có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {GM} + \overrightarrow {MA} + \overrightarrow {GM} + \overrightarrow {MB} + \overrightarrow {GM} + \overrightarrow {MC} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow {MC} - 3\overrightarrow {GM} \)

Xét \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {MC} - 3\overrightarrow {GM} = \overrightarrow 0 \Rightarrow \overrightarrow {MC} = 3\overrightarrow {GM} \)

Suy ra M là điểm nằm giữa C và G sao cho \(MG = \frac{1}{4}CG\).

b) Ta có: \[\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} \]

\[ = \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {OM} + \overrightarrow {MB} + 2\overrightarrow {OM} + 2\overrightarrow {MC} \]

\[ = 4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right)\]

\[ = 4\overrightarrow {OM} + \overrightarrow 0 = 4\overrightarrow {OM} \].

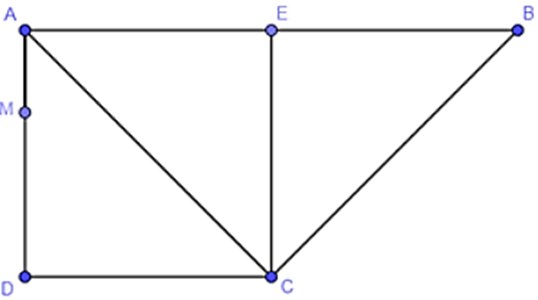
Gọi E là chân đường vuông góc hạ từ C xuống AB

Tứ giác ADCE là hình vuông Þ CE = 3a

\( \Rightarrow CE = \frac{1}{2}AB\) Þ ∆ACB vuông tại C

Theo định lý Py-ta-go ta tính được \(AC = CB = 3\sqrt 2 a\)

\(T = \left( {\overrightarrow {MB} + 2\overrightarrow {MC} } \right)\,.\,\overrightarrow {CB} = \left( {\overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {MA} + 2\overrightarrow {AC} } \right)\,.\,\overrightarrow {CB} \)

\( = \left( {3\overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {AC} } \right)\,.\,\overrightarrow {CB} \)

\( = \left( {\overrightarrow {DA} + \overrightarrow {AB} + 2\overrightarrow {AC} } \right)\,.\,\overrightarrow {CB} \)

\( = \overrightarrow {DA} \,.\,\overrightarrow {CB} + \overrightarrow {AB} \,.\,\overrightarrow {CB} + 2\overrightarrow {AC} \,.\,\overrightarrow {CB} \)

\( = 3a.\,3\sqrt 2 a\,.\,\cos 45^\circ + 6a.\,3\sqrt 2 a\,.\,\cos 45^\circ + 2AC.\,CB\,.\,\cos 90^\circ \)

= 27a²

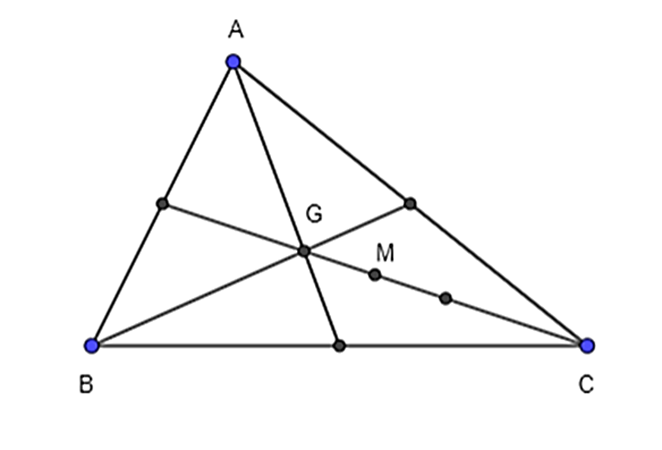
a) Gọi G là trọng tâm tam giác ABC, có:

\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {GM} + \overrightarrow {MA} + \overrightarrow {GM} + \overrightarrow {MB} + \overrightarrow {GM} + \overrightarrow {MC} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow {MC} - 3\overrightarrow {GM} \)

Xét \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {MC} - 3\overrightarrow {GM} = \overrightarrow 0 \Rightarrow \overrightarrow {MC} = 3\overrightarrow {GM} \)

Suy ra M là điểm nằm giữa C và G sao cho \(MG = \frac{1}{4}CG\)

b) Ta có: \[\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} \]

\[ = \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {OM} + \overrightarrow {MB} + 2\overrightarrow {OM} + 2\overrightarrow {MC} \]

\[ = 4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right)\]

\[ = 4\overrightarrow {OM} + \overrightarrow 0 = 4\overrightarrow {OM} \]

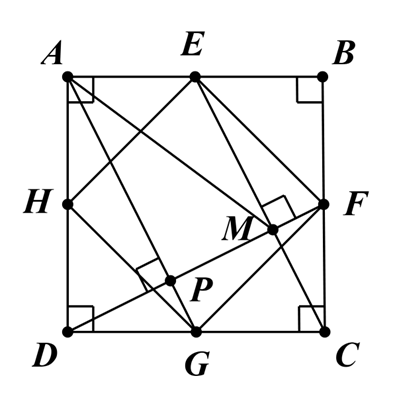
a) Xét ∆AEH và ∆BEF, có:

AE = BE (E là trung điểm AB);

AH = BF (do \(AH = \frac{1}{2}AD,\;BF = \frac{1}{2}BC\) và AD = BC);

\(\widehat {HAE} = \widehat {EBF} = 90^\circ \)

Do đó ∆AEH = ∆BEF (c.g.c).

Suy ra HE = EF (cặp cạnh tương ứng).

Chứng minh tương tự, ta được EF = GF và GH = GF.

Do đó tứ giác EFGH là hình thoi (1)

Ta có BE = BF (do \(BE = \frac{1}{2}AB,\;BF = \frac{1}{2}BC\) và AB = BC)

và \(\widehat {EBF} = 90^\circ \) (do ABCD là hình vuông).

Suy ra ∆BEF vuông cân tại B.

Do đó \(\widehat {BEF} = 45^\circ \)

Chứng minh tương tự, ta được \(\widehat {AEH} = 45^\circ \)

Ta có \(\widehat {AEH} + \widehat {HEF} + \widehat {FEB} = 180^\circ \) (kề bù).

\( \Leftrightarrow \widehat {HEF} = 180^\circ - \widehat {AEH} - \widehat {FEB} = 180^\circ - 45^\circ - 45^\circ = 90^\circ \;\left( 2 \right)\)

Từ (1), (2), suy ra tứ giác EFGH là hình vuông.

b) Xét ∆CBE và ∆DCF, có:

CB = DC (ABCD là hình vuông);

\(\widehat {CBE} = \widehat {DCF} = 90^\circ \)

BE = CF (do \(BE = \frac{1}{2}AB,\;CF = \frac{1}{2}BC\) và AB = BC).

Do đó ∆CBE = ∆DCF (c.g.c).

Suy ra \(\widehat {ECB} = \widehat {FDC}\) (cặp góc tương ứng).

Mà \(\widehat {DFC} + \widehat {FDC} = 90^\circ \) (∆DFC vuông tại C).

Do đó \(\widehat {DFC} + \widehat {ECB} = 90^\circ \)

Tam giác CFM, có: \(\widehat {CMF} = 180^\circ - \left( {\widehat {DFC} + \widehat {ECB}} \right) = 90^\circ \)

Vậy DF ^ CE tại M.

Gọi P là giao điểm của AG và DF.

Chứng minh tương tự như trên, ta được AG ^ DF tại P.

Mà CE ^ DF (chứng minh trên).

Suy ra CE // AG.

∆DMC có: G là trung điểm của DC (giả thiết) và PG // MC (chứng minh trên).

Suy ra GP là đường trung bình của ∆DMC.

Do đó P là trung điểm DM.

∆AMD có: AP vừa là đường trung tuyến, vừa là đường cao.

Vậy ∆AMD cân tại A.

c) Xét ∆DMC và ∆DCF, có:

\(\widehat {MDC}\) chung;

\(\widehat {DMC} = \widehat {DCF} = 90^\circ \)

Do đó ∆DMC ᔕ ∆DCF (g.g).

Suy ra \(\frac{{DM}}{{DC}} = \frac{{MC}}{{CF}} = \frac{{DC}}{{DF}}\) (*)

Ta có \({S_{DMC}} = \frac{1}{2}MC\,.\,MD\) và \({S_{DCF}} = \frac{1}{2}DC\,.\,CF\)

Suy ra \(\frac{{{S_{DMC}}}}{{{S_{DCF}}}} = \frac{{MC\,.\,MD}}{{DC\,.\,CF}} = \frac{{D{M^2}}}{{D{C^2}}}\)

Do đó \({S_{DMC}} = \frac{{D{M^2}}}{{D{C^2}}}.\,{S_{DCF}} = \frac{{D{M^2}}}{{D{C^2}}}.\,\frac{1}{2}CD\,.\,CF = \frac{{D{M^2}}}{{{a^2}}}\,.\,\frac{1}{2}a\,.\,\frac{a}{2} = \frac{{D{M^2}}}{4}\)

Tam giác CDF vuông tại C:

\(DF = \sqrt {D{C^2} + C{F^2}} = \sqrt {D{C^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\)

Từ (*), ta có: DM.DF = DC².

\( \Leftrightarrow DM\,.\,\frac{{a\sqrt 5 }}{2} = {a^2}\)

\( \Rightarrow DM\, = \frac{{2a\sqrt 5 }}{5}\)

Vậy \({S_{DMC}} = \frac{{D{M^2}}}{4} = {\left( {\frac{{2a\sqrt 5 }}{5}} \right)^2}\,.\,\frac{1}{4} = \frac{{{a^2}}}{5}\).

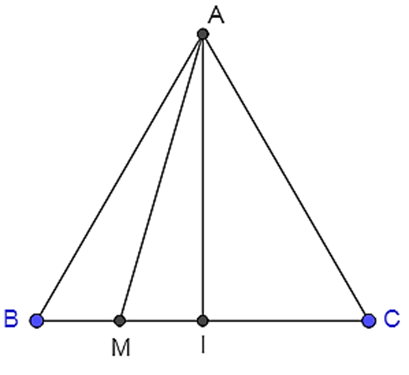
Gọi M là trung điểm của BI

\( \Rightarrow MI = \frac{1}{4}BC = \frac{a}{4}\)

Ta có: \(\overrightarrow {AB} + \overrightarrow {AI} = 2\overrightarrow {AM} \)

\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AI} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM\)

Xét ∆AMI có: AI ^ BC

\(AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)

\(MI = \frac{a}{4}\)

\( \Rightarrow AM = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{a}{4}} \right)}^2}} = \frac{{a\sqrt {13} }}{4}\)

\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AI} } \right| = \left| {2\overrightarrow {AM} } \right| = \frac{{a\sqrt {13} }}{2}\)

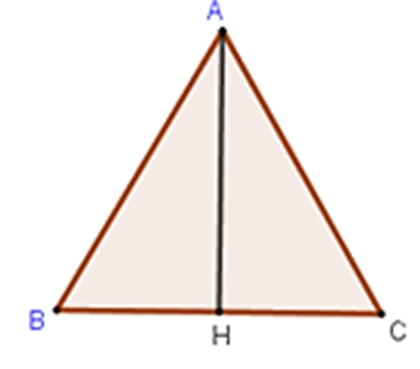
Tam giác ABC đều cạnh a, trung điểm H của BC nên AC = AB = BC = a và \(BH = HC = \frac{a}{2}\)

Tam giác ABH vuông tại H nên

\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\)

Do đó \(\left| {\overrightarrow {HB} } \right| = HB = \frac{a}{2}\) nên A đúng.

\(\left| {\overrightarrow {AH} } \right| = AH = \frac{{a\sqrt 3 }}{2}\) nên B đúng.

\(\left| {\overrightarrow {CH} } \right| = CH = \frac{a}{2}\) nên C sai.

\(\left| {\overrightarrow {BH} } \right| = \left| {\overrightarrow {HC} } \right| = \frac{a}{2}\) nên D đúng.

Đáp án cần chọn là: C

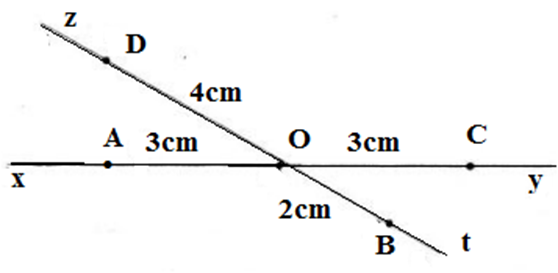
Các bạn vẽ hình theo các bước:

• Vẽ hai đường thẳng xy và zt cắt nhau tại O

• Trên đường thẳng xy:

Lấy A thuộc tia Ox, lấy C thuộc tia Oy sao cho OA = OC = 3 cm.

• Trên đường thẳng zt:

+ Lấy B thuộc tia Ot sao cho OB = 2 cm

+ Lấy D thuộc tia Oz sao cho OD = 2OB = 2 . 2 = 4 (cm).

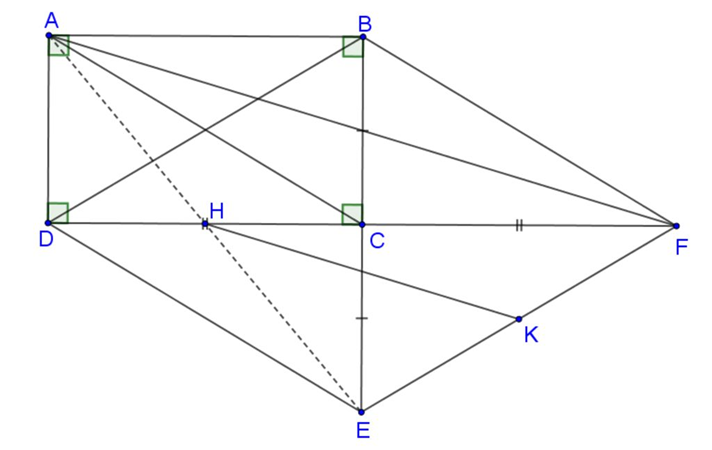
a) Xét tứ giác BDEF, ta có:

C là trung điểm của BE (vì E đối xứng B qua C)

C là trung điểm của DF (vì F đối xứng D qua C)

Nên tứ giác BDEF là hình bình hành

Lại có BE ^ DF tại C (vì ABCD là hình chữ nhật)

Vậy BDEF là hình thoi

b) Ta có AC = BD (vì ABCD là hình chữ nhật)

Mà BD = DE (vì BDEF là hình thoi)

Vậy AC = DE

c) Ta có AD = BC (vì ABCD là hình chữ nhật)

Mà BC = CE (vì E đối xứng B qua C)

Nên AD = CE

Xét tứ giác ADEC, ta có:

AC = DE(cmt)

AD = CE(cmt)

 Nên tứ giác ADEC là hình bình hành

Lại có H là trung điểm của CD

Do đó H cũng là trung điểm của AE

Xét ∆AEF, ta có:

H là trung điểm của AE (cmt)

K là trung điểm của EF (gt)

Nên HK là đường trung bình của ∆AEF

Do đó HK // AF

d) Ta có S_∆AEF = S_∆AHF + S_∆EHF

\( \Rightarrow 30 = \frac{1}{2}AD\,.\,HF + \frac{1}{2}EC\,.\,HF\)

\( \Rightarrow \frac{1}{2}HF\,.\,\left( {AD + EC} \right) = 30\)

Þ HF.(AD + AD) = 60

Þ 2HF.AD = 60

\( \Rightarrow 2\,.\,\frac{3}{2}CD\,.\,AD = 60\)

Þ CD.AC = 20

Þ S_ABCD = 20 (cm²)

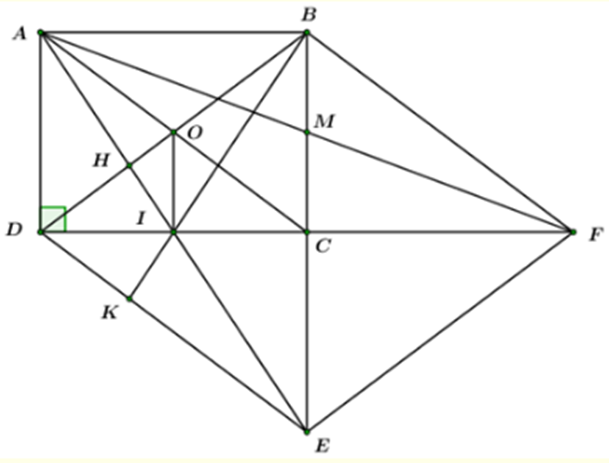
a) Ta có: E là điểm đối xứng với B qua C

Suy ra C là trung điểm của BE nên BC = EC

Xét tứ giác ACED ta có:

AD // EC (AD // BC)

AD = CE (= BC)

Suy ra ACED là hình bình hành.

b) Xét ∆ABM và ∆FCM ta có:

\[\widehat {ABM} = \widehat {FCM} = 90^\circ \]

MB = MC (gt)

\(\widehat {AMB} = \widehat {CMF}\) (Hai góc đối đỉnh)

Þ ∆ABM = ∆FCM (g.c.g)

Þ AB = CF (hai cạnh tương ứng)

Mà AB = DC (gt) Þ DC =F

Xét tứ giác BDEF ta có:

BE ^ DF

BE Ç DF = C

C là trung điểm của BE và DF

Þ BDEF là hình thoi

c) Gọi AC Ç BD = H; AI Ç BD = O

Ta có: ACED là hình bình hành

Mà AE Ç CD = I

Þ I là trung điểm của CD

Lại có O là trung điểm của AC

Þ H là trực tâm của ∆ACD

\( \Rightarrow \frac{{IH}}{{AI}} = \frac{1}{3}\)

Mà I là trung điểm của AE \( \Rightarrow AI = \frac{1}{2}AE \Rightarrow IH = \frac{1}{6}AE\)

Ta có: BDEF là hình thoi

Þ DF là tia phân giác của \(\widehat {BDE}\) (tính chất hình thoi)

\( \Rightarrow \widehat {BDC} = \widehat {CDE}\)

Ta có BDEF là hình thoi

Þ BD = DE (hai cạnh bên)

Xét ∆BDI và ∆EDI ta có:

DI chung

\(\widehat {IDB} = \widehat {IDE}\) (cmt)

BD = DE (cmt)

Þ ∆BDI = ∆EDI (c.g.c)

\( \Rightarrow \widehat {DBI} = \widehat {DEI}\) (hai góc tương ứng)

Và IE = IB (hai cạnh tương ứng)

Xét ∆HBI và ∆KEI ta có:

\(\widehat {HBI} = \widehat {KEI}\) (cmt)

IE = IB (cmt)

\(\widehat {HIB} = \widehat {KIE}\) (hai góc đối đỉnh)

Do đó ∆HBI = ∆KEI (g.c.g)

Suy ra HI = IK (hai cạnh tương ứng).

Vậy \(IK = \frac{1}{6}AE\) (đpcm)

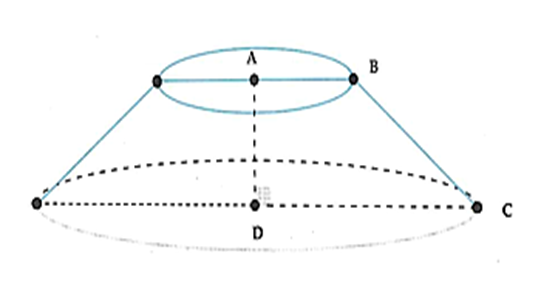
Khi cho hình thang ABCD quay quanh trục AD ta thu được khối nón cụt có đường cao AD, bán kính của đáy lớn là DC, bán kính đáy nhỏ là AB.

Áp dụng công thức tích thể tích khối nón cụt, ta có thể tích của khối tròn xoay tạo thành là:

\(V = \frac{1}{3}h.\pi \left( {{R_1}^2 + {R_2}^2 + {R_1}.{R_2}} \right)\)

\( = \frac{1}{3}AD.\pi \left( {A{B^2} + D{C^2} + AB\,.\,DC} \right)\)

\( = \frac{1}{3}\,.\,a\,.\,\pi \left( {{a^2} + 4{a^2} + a\,.\,2a} \right) = \frac{{7\pi {a^3}}}{3}\)

Vậy thể tích khối tròn xoay là \(\frac{{7\pi {a^3}}}{3}\).

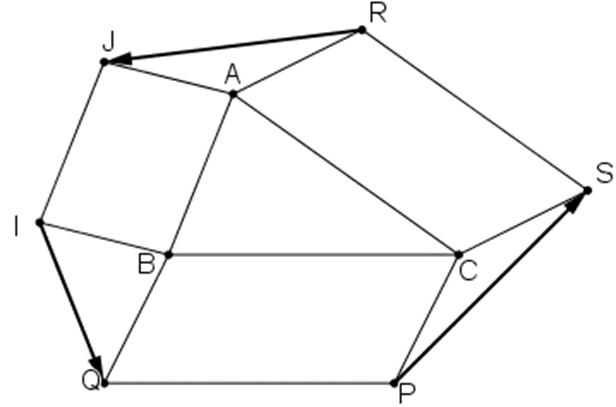
Ta có: AJIB là hình bình hành nên \(\overrightarrow {AJ} = \overrightarrow {BI} \)

\( \Rightarrow \overrightarrow {AJ} + \overrightarrow {IB} = \overrightarrow {BI} + \overrightarrow {IB} = \overrightarrow {BB} = \overrightarrow 0 \)

Tương tự như vậy:

• BCPQ là hình bình hành nên \(\overrightarrow {BQ} + \overrightarrow {PC} = \overrightarrow 0 \)

• CARS là hình bình hành nên \(\overrightarrow {CS} + \overrightarrow {RA} = \overrightarrow 0 \)

Do đó: \(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PQ} \)

\( = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)

\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right)\)

\( = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)

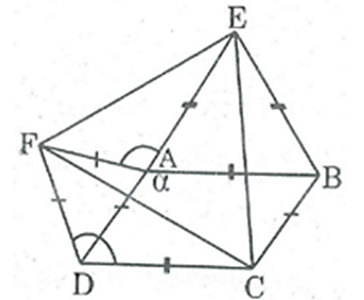
Ta có: \(\widehat {BAD} + \widehat {ADC} = 180^\circ \) (hai góc trong cùng phía bù nhau)

\( \Rightarrow \widehat {ADC} = 180^\circ - \widehat {BAD} = 180^\circ - \alpha \)

\(\widehat {CDF} = \widehat {ADC} + \widehat {ADF} = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \)

Suy ra: \(\widehat {CDF} = \widehat {EAF}\)

 Xét ∆AEF và ∆DCF:

AF = DF (Vì ∆ADF đều)

AE = DC (vì cùng bằng AB)

\(\widehat {CDF} = \widehat {EAF}\) (chứng minh trên)

Do đó: ∆AEF = ∆DCF (c.g.c) Þ EF = CF (1)

\(\widehat {CBE} = \widehat {ABC} + 60^\circ = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \)

Xét ∆BCE và ∆DFC: BE = CD ( vì cùng bằng AB)

\(\widehat {CBE} = \widehat {CDF} = 240^\circ - \alpha \)

BC = DF (vì cùng bằng AD)

Do đó ∆BCE = ∆DFC (c.g.c) Þ CE = CF (2)

Từ (1) và (2) suy ra: EF = CF = CE

Vậy ∆ECF đều.

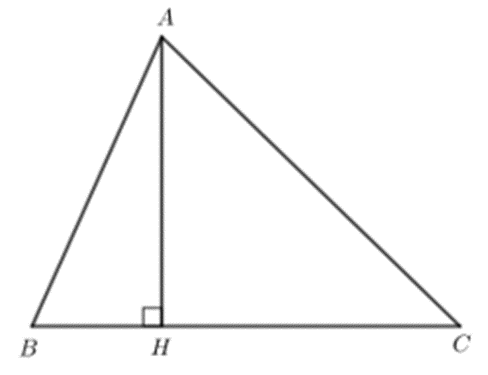
Tam giác ABH vuông tại H nên \(\widehat {AHB} = 90^\circ \) là góc lớn nhất trong tam giác ABH.

Do đó cạnh AB là cạnh lớn nhất trong tam giác ABH.

Suy ra AH < AB (1).

Tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB (2).

Từ (1) và (2) ta có AH < AB < AC.

Thứ tự độ tăng dần các đoạn thẳng AB, AH, AC là AH; AB; AC.

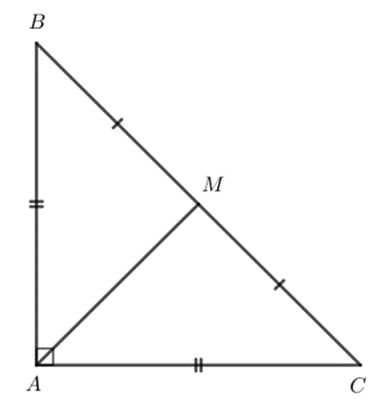
Xét ∆AMB và ∆AMC có:

AM chung

BM = CM (M là trung điểm của BC)

AB = AC (tam giác ABC cân tại A)

Suy ra ∆AMB = ∆AMC (c.c.c)

Do đó \(\widehat {MAB} = \widehat {MAC}\) (2 góc tương ứng)

Mà \(\widehat {MAB} + \widehat {MAC} = 90^\circ \) nên \(\widehat {MAB} = \widehat {MAC} = 45^\circ \)

Tam giác ABC vuông cân tại A nên \(\widehat {ABC} = \widehat {ACB}\) và \(\widehat {ABC} + \widehat {ACB} = 90^\circ \)

Suy ra \(\widehat {ABC} = \widehat {ACB} = 45^\circ \)

Tam giác MAB có \(\widehat {MAB} = \widehat {MBA} = 45^\circ \) nên tam giác MAB cân tại M (1)

Xét tam giác MAB có: \(\widehat {AMB} = 180^\circ - \widehat {MBA} - \widehat {MAB} = 180^\circ - 45^\circ - 45^\circ = 90^\circ \)

Suy ra AM ^ BM hay tam giác MAB vuông tại M (2)

Từ (1) và (2) suy ra tam giác MAB vuông cân tại M.

Vậy tam giác MAB vuông cân tại M.

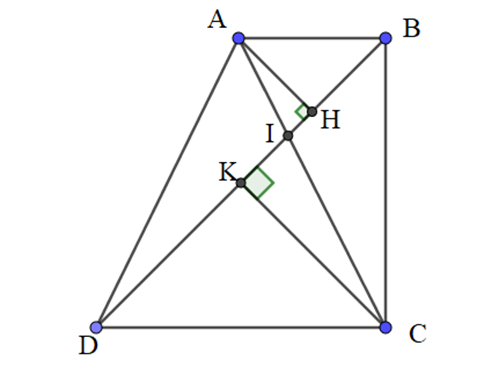
S_ABCD = S_IAB + S_IBC + S_ICD + S_IDA

\( = \frac{1}{2}IA\,.\,IB\,.\,\sin \widehat {AIB} + \frac{1}{2}IB\,.\,IC\,.\,\sin \widehat {BIC} + \frac{1}{2}IC\,.\,ID\,.\,\sin \widehat {CID} + \frac{1}{2}ID\,.\,IA\,.\,\sin \widehat {DIA}\)

\( = \frac{1}{2}IA\,.\,IB\,.\,\sin \alpha + \frac{1}{2}IB\,.\,IC\,.\,\sin \alpha + \frac{1}{2}IC\,.\,ID\,.\,\sin \alpha + \frac{1}{2}ID\,.\,IA\,.\,\sin \alpha \)

\( = \frac{1}{2}\sin \alpha \left( {IA\,.\,IB\, + IB\,.\,IC\, + IC\,.\,ID\, + ID\,.\,IA} \right)\)

\[ = \frac{1}{2}\sin \alpha \left[ {IB\,\left( {IA\, + IC} \right)\, + ID\,\left( {IA\, + IC} \right)\,} \right]\]

\[ = \frac{1}{2}\sin \alpha \left( {IB + ID} \right)\left( {IA\, + IC} \right)\]

\[ = \frac{1}{2}AC\,.\,BD\,.\,\sin \alpha \]

\[ = \frac{1}{2}m\,.\,n\,.\,\sin \alpha \].

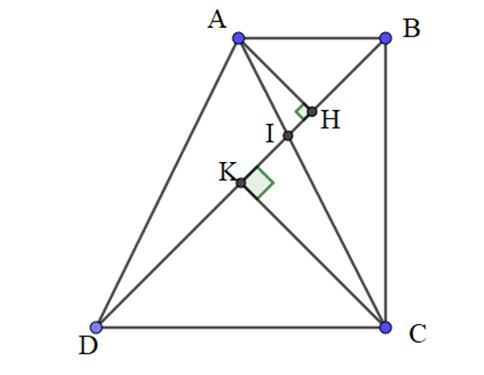
Ta có: sin α = sin (180° − α)

S_ABCD = S_IAB + S_IBC + S_ICD + S_IDA

\( = \frac{1}{2}IA\,.\,IB\,.\,\sin \widehat {AIB} + \frac{1}{2}IB\,.\,IC\,.\,\sin \widehat {BIC} + \frac{1}{2}IC\,.\,ID\,.\,\sin \widehat {CID} + \frac{1}{2}ID\,.\,IA\,.\,\sin \widehat {DIA}\)

\( = \frac{1}{2}IA\,.\,IB\,.\,\sin \alpha + \frac{1}{2}IB\,.\,IC\,.\,\sin \alpha + \frac{1}{2}IC\,.\,ID\,.\,\sin \alpha + \frac{1}{2}ID\,.\,IA\,.\,\sin \alpha \)

\( = \frac{1}{2}\sin \alpha \left( {IA\,.\,IB\, + IB\,.\,IC\, + IC\,.\,ID\, + ID\,.\,IA} \right)\)

\[ = \frac{1}{2}\sin \alpha \left[ {IB\,\left( {IA\, + IC} \right)\, + ID\,\left( {IA\, + IC} \right)\,} \right]\]

\[ = \frac{1}{2}\sin \alpha \left( {IB + ID} \right)\left( {IA\, + IC} \right)\]

\[ = \frac{1}{2}AC\,.\,BD\,.\,\sin \alpha \] (đpcm)