Giải bởi Vietjack
Lời giải
Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.
Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\end{array} \right.\).
Theo đề, ta có từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B.
⇒ Từ x tấn nguyên liệu loại I, có thể chiết xuất được 20x kg chất A và 0,6x kg chất B.
Theo đề, ta có từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B.
⇒ Từ y tấn nguyên liệu loại II, có thể chiết xuất được 10y kg chất A và 1,5y kg chất B.
Như vậy ta chiết xuất được 20x + 10y (kg) chất A và 0,6x + 1,5y (kg) chất B.
Khi đó ta có hệ điều kiện là:
\(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\20x + 10y \ge 140\\0,6x + 1,5y \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\,\,\,\,\,\left( * \right)\)
Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 4x + 3y đạt giá trị nhỏ nhất.
Vẽ và xác định miền nghiệm của (*):
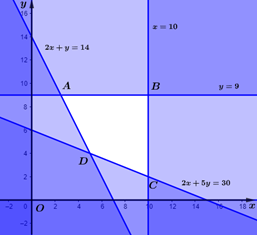
Ta có:
⦁ Miền nghiệm của (*) là tứ giác ABCD (kể cả biên).
⦁ \(A\left( {\frac{5}{2};9} \right),\,B\left( {10;9} \right),\,C\left( {10;2} \right),\,D\left( {5;4} \right)\).
⦁ F(A) = 37, F(B) = 67, F(C) = 46, F(D) = 32.
Suy ra minF(x; y) = F(D) = 32 khi và chỉ khi x = 5, y = 4.
Vậy để chi phí mua nguyên liệu là ít nhất thì cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.
Do đó ta chọn phương án A.Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC = AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng: MA2 = MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM // EF.
Cho tam giác ABC có AB = 2, AC = 3, \[\widehat {BAC} = 60^\circ \]. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn \(\overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AC} \).
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
b) Biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {BD} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
c) Chứng minh AM ⊥ BD.
Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:
a) Giỏi cả ba môn.
b) Giỏi đúng 1 môn.
