Phương trình: |x| + 1 = x2 + m có 1 nghiệm duy nhất khi và chỉ khi:
A. m = 0
B. m = 1
C. m = −1
D. Không tồn tại giá trị m thỏa mãn
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: D
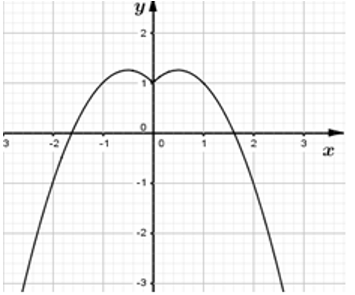
|x| + 1 = x2 + m ⇔ m = f(x) =
Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số y = −x2 + x + 1
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại m để phương trình m = f(x) có duy nhất 1 nghiệm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình mx2 – mx + 1 = 0 có nghiệm.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc [−20; 20] để phương trình x2 − 2mx + 144 = 0 có nghiệm. Tổng của các phần tử trong S bằng:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn
[−5; 10] để phương trình (m + 1)x = (3m2 − 1)x + m − 1 có nghiệm duy nhất. Tổng các phần tử trong S bằng:
Tìm tất cả các giá trị thực của tham số m để phương trình có một nghiệm gấp đôi nghiệm còn lại
Gọi S là tập hợp các giá trị nguyên của tham số m thuộc đoạn [−3; 5] để phương trình có nghiệm. Tổng các phần tử trong tập S bằng:
Có bao nhiêu giá trị nguyên của m để phương trình:
có đúng 3 nghiệm thuộc
Giả sử các phương trình sau đây đều có nghiệm. Nếu biết các nghiệm của phương trình: x2 + px + q = 0 là lập phương các nghiệm của phương trình x2 + mx + n = 0. Thế thì: