Đáp án cần chọn là: D

Phương trình có nghiệm khi Δ' = m² – 144 ≥ 0 ⇔ m² ≥ 12² ⇔  $\left[\begin{array}{c}m\ge 12\\ m\le -12\end{array}\right.$

Mà m ∈ Z và m ∈ [−20; 20] ⇒ S = {−20; −19; −18;...; −12; 12; 13; 14;...; 20}

Do đó tổng các phần tử trong tập S bằng 0.

Đáp án cần chọn là: A

Ta có: $\left\{\begin{array}{c}S=x_1+x_2=\left(1-\sqrt{2}\right)+\left(1+\sqrt{2}\right)=2\\ P=x_1.x_2=\left(1-\sqrt{2}\right).\left(1+\sqrt{2}\right)=-1\end{array}\right.$ 

⇒ PT: x² – Sx + P = 0 ⇔ x² − 2x – 1 = 0.

Đáp án cần chọn là: B

Phương trình viết lại (3m² – m − 2)x = 1 − m.

Phương trình đã cho có nghiệm duy nhất khi 3m² – m – 2 ≠ 0 ⇔  $\left\{\begin{array}{c}m\ne 1\\ m\ne -\frac{2}{3}\end{array}\right.$

Do m ∈ Z và m ∈ [−5; 10] ⇒ m ∈ {−5; −4; −3; −2; −1; 0; 2; 3; 4; 5; 6; 7; 8; 9; 10}.

Do đó, tổng các phần tử trong S bằng 39.

Đáp án cần chọn là: C

Phương trình  $\iff \left\{\begin{array}{c}4x-17\ge 0\\ {\left|x^2-4x-5\right|}^2={\left(4x-17\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{c}x\ge \frac{17}{4}\\ {\left(x^2-4x-5\right)}^2={\left(4x-17\right)}^2\end{array}\right.$

$\begin{array}{l}\iff \left\{\begin{array}{c}x\ge \frac{17}{4}\\ (x^2-8x+12)(x^2-22)=0\end{array}\right.\iff \left\{\begin{array}{c}x\ge \frac{17}{4}\\ \left[\begin{array}{c}{x}^2-8x+12=0\\ x^2-22=0\end{array}\right.\end{array}\right.\\ \iff \left\{\begin{array}{c}x\ge \frac{17}{4}\\ \left[\begin{array}{c}x=2\vee x=6\\ x=\pm \sqrt{22}\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}x=6\\ x=\sqrt{22}\end{array}\right.\\ \Rightarrow P={\left(\sqrt{22}\right)}^2+6=28\end{array}$

Đáp án cần chọn là: A

Điều kiện:  $\left\{\begin{array}{c}3x^2+6x+16\ge 0\\ x^2+2x\ge 0\\ x^2+2x+4\ge 0\end{array}\right.\iff \left[\begin{array}{c}x\le -2\\ x\ge 0\end{array}\right.$

Đặt  $t=\sqrt{x^2+2x}(t\ge 0)\iff t^2=x^2+2x$

Phương trình trở thành:  $\sqrt{3t^2+16}+t=2\sqrt{t^2+4}$

  $\begin{array}{l}\iff 3t^2+16+t^2+2t\sqrt{3t^2+16}=4t^2+16\\ \iff 2t\sqrt{3t^2+16}=0\\ \iff t=0\end{array}$

Với $t=0\iff x^2+2x=0\iff \left[\begin{array}{c}x=0\\ x=-2\end{array}\right.$

Vậy tập nghiệm của phương trình là: S =$\left\{0;-2\right\}$

Đáp án cần chọn là: D

Trường hợp 1: x < −2

Phương trình thành 3 – x – 2x – 4 = 3 ⇔ 3x = −4 ⇔ x = −$\frac{4}{3}$  (l)

Trường hợp 2: −2 ≤ x ≤ 3

Phương trình thành 3 – x + 2x + 4 = 3 ⇔ x = −4 (l)

Trường hợp 3: x > 3

Phương trình thành x – 3 + 2x + 4 = 3 ⇔ 3x = 2 ⇔ x =$\frac{2}{3}$ (l)

Vậy S = ∅

Đáp án cần chọn là: D

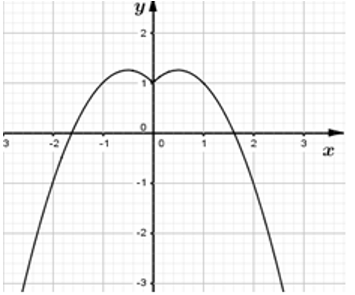
|x| + 1 = x² + m ⇔ m = f(x) =  $\left\{\begin{array}{c}-x^2+x+1khix\ge 0\\ -x^2-x+1khix<0\end{array}\right.$

Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:

+ Vẽ đồ thị hàm số y = −x² + x + 1

+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.

+ Xóa bỏ phần bên trái trục tung trước đó đi.

Dựa vào đồ thị ta suy ra không tồn tại m để phương trình m = f(x) có duy nhất 1 nghiệm.

Đáp án cần chọn là: D

$\frac{x-m}{x+1}=\frac{x-2}{x-1}$$\iff \left\{\begin{array}{c}x\ne \pm 1\\ mx=m+2\end{array}\right.$

Phương trình đã cho có nghiệm  $\Rightarrow \left\{\begin{array}{c}m\ne 0\\ x=1+\frac{2}{m}\ne \pm 1\end{array}\right.\iff \left\{\begin{array}{c}m\ne 0\\ m\ne -1\end{array}\right.$

Vì m ∈ Z, m ∈ [−3; 5] nên m ∈ S = {−3; −2; 1; 2; 3; 4; 5}.

Đáp án cần chọn là: D

Ta có:  $\Delta ={\left(4m-1\right)}^2-\mathrm{4.2.}\left(2m-1\right)={\left(4m-3\right)}^2$

$2{\left(x^2+2x\right)}^2-\left(4m-1\right)\left(x^2+2x\right)+2m-1=0\iff \left[\begin{array}{c}{x}^2+2x=\frac{1}{2}\left(1\right)\\ x^2+2x=2m-1\left(2\right)\end{array}\right.$

$\left(1\right)\iff x^2+2x-\frac{1}{2}=0\iff \left[\begin{array}{c}x=\frac{-2+\sqrt{6}}{2}\notin \left[-3;0\right]\\ x=\frac{-2-\sqrt{6}}{2}\in \left[-3;0\right]\end{array}\right.$

Do đó (1) chỉ có 1 nghiệm thuộc $\left[-3;0\right]$

Để phương trình đã cho có 3 nghiệm thuộc đoạn $\left[-3;0\right]$ thì phương trình (2) phải có hai nghiệm phân biệt thuộc đoạn $\left[-3;0\right]$và hai nghiệm này phải khác $\frac{-2-\sqrt{6}}{2}$

(2) $\iff {\left(x+1\right)}^2=2m$

Phương trình (2) có hai nghiệm phân biệt khác $\frac{-2-\sqrt{6}}{2}$ và thuộc đoạn $\left[-3;0\right]$

$\iff \left\{\begin{array}{c}2m>0\\ {\left(\frac{-2-\sqrt{6}}{2}+1\right)}^2\ne 2m\\ -3\le -1+\sqrt{2m}\le 0\\ -3\le -1-\sqrt{2m}\le 0\end{array}\right.\iff \left\{\begin{array}{c}m>0\\ m\ne \frac{3}{4}\\ m\le \frac{1}{2}\\ m\le 2\end{array}\right.$

Không có giá trị nào của m nguyên thỏa mãn.

Đáp án cần chọn là: C

Điều kiện: 12 – x ≥ 0 ⇔ x ≤ 12

Đặt $\sqrt[3]{x+24}=u;\sqrt{12-x}=v$  ⇒ Hệ phương trình: $\left\{\begin{array}{c}u+v=6\left(1\right)\\ u^3+v^2=36\left(2\right)\end{array}\right.$ 

 Từ (1) ⇒ v = 6 – u. Thay vào (2) ta được:

u³ + (6 − u)² = 36 ⇔ u³ + u² − 12u = 0 ⇔ u(u² + u − 12) = 0 

+) Với u = 0 $\iff \sqrt[3]{x+24}=0$ ⇔ x = −24 (tm)

+) Với u = 3 ⇔ $\sqrt[3]{x+24}=3$ ⇔ x + 24 = 27 ⇔ x = 3 (tm)

+) Với u = −4 ⇔ $\sqrt[3]{x+24}=-4$ ⇔ x + 24 = −64 ⇔ x = −88 (tm)

Vậy phương trình có 3 nghiệm.

Đáp án cần chọn là: B

Điều kiện: x > 0

Ta có:  $5\sqrt{x}+\frac{5}{2\sqrt{x}}=2x+\frac{1}{2x}+4$ $\iff$ $5(\sqrt{x}+\frac{1}{2\sqrt{x}})=2(x+\frac{1}{4x})+4$

Đặt $\sqrt{x}+\frac{1}{2\sqrt{x}}=t(t>0)\iff t^2=x+\frac{1}{4x}+1\iff x+\frac{1}{4x}=t^2-1$

Khi đó phương trình trở thành:  $5t=2(t^2-1)+4\iff 2t^2-5t+2=0$

$\iff \left[\begin{array}{c}t=2\left(tm\right)\\ t=\frac{1}{2}\left(tm\right)\end{array}\right.$

+ Với  $t=\frac{1}{2}\Rightarrow x+\frac{1}{4x}=-\frac{3}{4}\iff 4x^2+3x+1=0$ (vô nghiệm)

+ Với $t=2\Rightarrow x+\frac{1}{4x}=3\iff 4x^2-12x+1=0$ có hai nghiệm phân biệt

Vậy tổng 2 nghiệm của phương trình là: 3

Đáp án cần chọn là: A

Nếu m = 0 thì phương trình trở thành 1 = 0: vô nghiệm.

Khi m ≠ 0, phương trình đã cho có nghiệm khi và chỉ khi

      Δ = m² − 4m ≥ 0 ⇔  $\left[\begin{array}{c}m\le 0\\ m\ge 4\end{array}\right.$

Kết hợp điều kiện m ≠ 0, ta được  $\left[\begin{array}{c}m<0\\ m\ge 4\end{array}\right.$

Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.

Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.

Đáp án cần chọn là: A

Phương trình có hai nghiệm phân biệt ⇔ Δ > 0

⇔ m² − 8m + 16 > 0 ⇔ (m − 4)² > 0 ⇔ m ≠ 4. (∗)

Theo định lí Viet và yêu cầu đề bài, ta có  $\left\{\begin{array}{c}{x}_1.x_2=\frac{m-1}{3};x_1+x_2=\frac{m+2}{3}\\ x_1=2x_2\end{array}\right.$

 $\iff \left\{\begin{array}{c}{x}_1=\frac{2}{9}(m+2),x_2=\frac{1}{9}(m+2)\\ x_1.x_2=\frac{m-1}{3}\end{array}\right.$

$\Rightarrow \text{\hspace{0.17em}}\frac{2}{81}{(m+2)}^2=\frac{m-1}{3}\iff 2m^2-19m+35=0\iff \left[\begin{array}{c}m=\frac{5}{2}\\ m=7\end{array}\right.$(thỏa mãn (*))

Đáp án cần chọn là: C

Gọi x₁, x₂ là nghiệm của x² + px + q = 0

Gọi x₃, x₄ là nghiệm của x² + mx + n = 0

- Khi đó, theo Vi-et: x₁ + x₂ = −p, x₃ + x₄ = −m, x₃.x₄ = n.

- Theo yêu cầu ta có:$\left\{\begin{array}{c}{x}_1=x_3^3\\ x_2=x_4^3\end{array}\right.\Rightarrow x_1+x_2=x_3^3+x_4^3\iff x_1+x_2={(x_3+x_4)}^3-3x_3{x}_4(x_3+x_4)$

⇒ −p = −m³ + 3mn⇒ p = m³ − 3mn.

Đáp án cần chọn là: B

Ta có: $x^2+\frac{4}{x^2}-4\left(x-\frac{2}{x}\right)+k-1=0$

$\iff {\left(x-\frac{2}{x}\right)}^2-4\left(x-\frac{2}{x}\right)+k+3=0\left(1\right)$

Đặt $t=x-\frac{2}{x}hay{x}^2-tx-2=0$, phương trình trở thành $t^2-4t+k+3=0$ (2)

Nhận xét: với mỗi nghiệm t của phương trình (2) cho ta hai nghiệm trái dấu của phương trình (1)

Ta có :

Δ′ = 4 − (k + 3) = 1 – k ⇒ phương trình (2) có hai nghiệm phân biệt

$t_1=2-\sqrt{1-k},t_2=2+\sqrt{1-k}$ với k < 1

+ Với $t_1=2-\sqrt{1-k}$ thì phương trình $x^2-\left(2-\sqrt{1-k}\right)x-2=0$ có 1 nghiệm

$x>1\iff af\left(1\right)<0\iff 1^2-\left(2-\sqrt{1-k}\right).1-2<0\iff k>-8$

+ Với $t_2=2+\sqrt{1-k}$ thì phương trình $x^2-\left(2+\sqrt{1-k}\right)x-2=0$ có 1 nghiệm

 $x>1\iff af\left(1\right)<0\iff 1^2-\left(2+\sqrt{1-k}\right).1-2<0\iff -3-\sqrt{1-k}<0$ (luôn đúng với k < 1)

Vậy kết hợp điều kiện k < 1 ta được -8 < k < 1