Đề kiểm tra Giữa Học kì 1 Vật lí 10 - Đề 02 có đáp án
-
1062 lượt thi
-
35 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Bước nào sau đây không có trong phương pháp tìm hiểu thế giới tự nhiên dưới góc độ vật lí.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương pháp tìm hiểu thế giới tự nhiên dưới góc độ vật lí được thực hiện theo tiến trình gồm các bước:
Bước 1: Quan sát, suy luận.
Bước 2: Đề xuất vấn đề.
Bước 3: Hình thành giả thuyết.
Bước 4: Kiểm tra giả thuyết
Bước 5: Rút ra kết luận.
Câu 2:
Đâu là sai số ngẫu nhiên khi đo tốc độ bằng đồng hồ bấm giây và thước đo chiều dài?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sai số ngẫu nhiên là kết quả của những thay đổi trong các lần đo do các điều kiện thay đổi ngẫu nhiên gây ra. Giá trị những sai lệch này khác nhau trong các lần đo. Tất cả các yếu tố như: thao tác bấm đồng hồ, vị trí đặt mắt nhìn thước, điều kiện thời tiết khi đo đều là các sai số ngẫu nhiên.
Câu 3:
Hai đại lượng nào sau đây là đại lượng vectơ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đại lượng vecto là đại lượng cho biết phương, chiều và độ lớn.
Độ dịch chuyển và vận tốc là các đại lượng vecto.
Câu 4:
Một vật chuyển động trên một đường thẳng Ox, chiều dương là chiều Ox. Trong một khoảng thời gian xác định, trường hợp nào sau đây độ lớn vận tốc trung bình của vật có thể nhỏ hơn tốc độ trung bình của nó?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nếu vật chuyển động dọc theo một đường thẳng mà không đổi chiều thì độ dịch chuyển và quãng đường đi được trong bất kì khoảng thời gian nào cũng như nhau. Kết quả là, độ lớn của vận tốc trung bình và tốc độ trung bình sẽ giống nhau. Tuy nhiên, nếu vật đảo ngược chiều chuyển động thì độ dịch chuyển sẽ nhỏ hơn quãng đường đi được. Trong trường hợp này, độ lớn của vận tốc trung bình sẽ nhỏ hơn tốc độ trung bình.
Câu 5:
Dùng một thước đo có chia độ đến milimét, đo 5 lần khoảng cách d giữa hai điểm A và B đều cho cùng một giá trị 1,245 m. Kết quả đo được viết
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
- Giá trị trung bình: d = 1,245 m.
- Sai số ngẫu nhiên: \[\overline {\Delta d} = 0\]
- Sai số hệ thống bằng nửa độ chia nhỏ nhất trên dụng cụ: Δd′ = 0,0005 m
\[ \Rightarrow \] Sai số của phép đo: \[\Delta d = \overline {\Delta d} + \Delta d' = 0 + 0,0005 = 0,0005\] m
\[ \Rightarrow \] Kết quả của phép đo: d = (1,245 ± 0,0005) m
Câu 6:
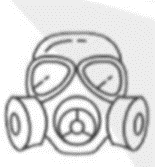
Biển báo dưới đây có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Biển báo có dạng nền trắng. Biển báo trên là biển báo đeo mặt nạ phòng độc
Câu 7:
Tốc độ trung bình được tính bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tốc độ trung bình được tính bằng quãng đường đi được chia cho khoảng thời gian đi hết quãng đường đó.
Câu 8:
Vận tốc được tính bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vận tốc được tính bằng độ dịch chuyển chia cho khoảng thời gian dịch chuyển.
Câu 9:
Tốc độ trung bình là đại lượng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tốc độ trung bình là đại lượng đặc trưng cho độ nhanh, chậm của chuyển động và được tính bằng thương số giữa quãng đường đi được với khoảng thời gian đi hết quãng đường đó.
Câu 10:
Một xe ô tô xuất phát từ tỉnh A, đi đến tỉnh B cách A 20 km; rồi lại trở về vị trí xuất phát ở tỉnh A. Kết luận nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ô tô đi từ A đến B, sau đó lại về A.
Quãng đường ô tô đó đi được là: 20 + 20 = 40 km
Vị trí đầu của ô tô là ở A. Vị trí cuối của ô tô vẫn là A.
Vậy độ dịch chuyển của ô tô bằng 0.
Câu 11:
Một con nhện bò dọc theo hai cạnh của một chiếc bàn hình chữ nhật. Biết hai cạnh bàn có chiều dài lần lượt là 0,8 m và 1,2 m. Độ dịch chuyển của con nhện khi nó đi được quãng đường 2,0 m là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Khi con nhện đi được quãng đường 2 m.
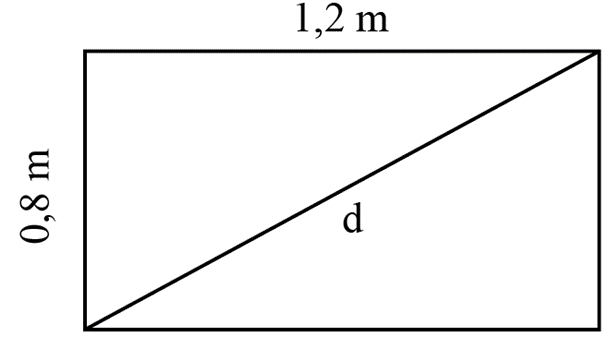
Độ dịch chuyển: \[d = \sqrt {0,{8^2} + 1,{2^2}} = 1,44\,m\]
Câu 12:
Sử dụng dữ liệu sau để trả lời các câu hỏi 12, 13, 14, 15.
Một xe máy chuyển động trên đường thẳng theo hướng từ Đông sang Tây. Sau một khoảng thời gian t1 là 20 phút, xe máy cách vị trí xuất phát 15 km. Tiếp sau đó một khoảng thời gian t2 là 30 phút, xe máy cách vị trí xuất phát là 35 km.
Độ dịch chuyển của xe máy từ thời điểm t1 đến t2 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Sau khoảng thời gian t1, xe máy cách vị trí xuất phát là 15 km.
Sau khoảng thời gian t2, xe máy cách vị trí xuất phát là 35 km.
Do đó, độ dịch chuyển của xe máy từ thời điểm t1 đến t2:
35 – 15 = 20 km.Câu 13:
Tốc độ của xe máy trong khoảng thời gian t1 là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quãng đường xe máy đã đi trong khoảng thời gian t1 là 15 km.
Thời gian xe máy đi là: 20 p = \[\frac{1}{3}\] h.
Tốc độ của xe máy trong khoảng thời gian t1 là:
\[{v_{tb}} = \frac{{{s_1}}}{{{t_1}}} = 15:\frac{1}{3} = 45\]km/h.
Câu 14:
Vận tốc của xe máy trong khoảng thời gian t2 là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Độ dịch chuyển của xe máy trong khoảng thời gian t2 là 20 km.
Khoảng thời gian dịch chuyển là 30 p = 0,5 h.
Vận tốc của xe máy trong khoảng thời gian này là:
\[v = \frac{d}{t} = \frac{{20}}{{0,5}} = 40\,km/h\]
Xe máy chuyển động theo hướng từ Đông sang Tây.
Nên vận tốc của xe là 40 km/h theo hướng Đông – Tây.
Câu 15:
Tốc độ trung bình của xe máy trên toàn bộ đoạn đường là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quãng đường xe máy đã đi là 35 km.
Thời gian xe máy đi hết quãng đường là: 20 + 30 = 50 p = \[\frac{5}{6}\] h.
Tốc độ trung bình của xe máy trên cả đoạn đường là: \[{v_{tb}} = \frac{s}{t} = 35:\frac{5}{6} = 42\]km/h
Câu 16:
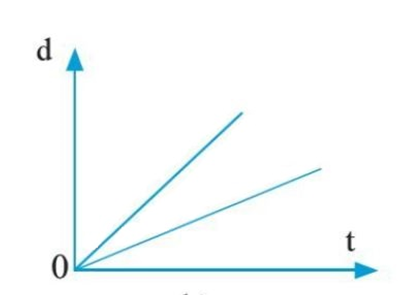
Đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng dưới đây, cho biết điều gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng là một đường thẳng xiên góc. Độ dốc của đường thẳng này cho biết giá trị của vận tốc.
Đồ thị trên có 2 đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng khác nhau, đường nào có độ dốc lớn hơn, thì có tốc độ lớn hơn.
Câu 17:
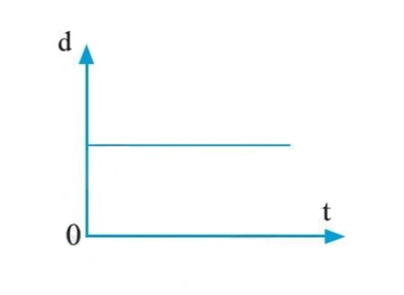
Đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng dưới đây, cho biết điều gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng là một đường thẳng xiên góc. Độ dốc của đường thẳng này cho biết giá trị của vận tốc.
Đồ thị trên có độ dốc bằng không, vật đứng yên.
Câu 18:
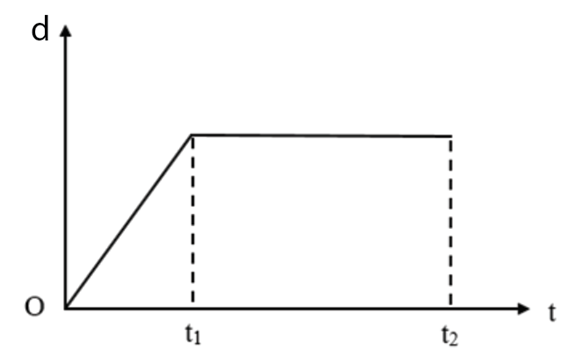
Đường biểu diễn độ dịch chuyển – thời gian của chuyển động thẳng của một chiếc xe có dạng như hình vẽ. Trong khoảng thời gian nào, tốc độ của xe không thay đổi?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trong khoảng thời gian từ O đến t1 đường biểu diễn là đường thẳng xiên góc, độ dịch chuyển tăng đều, khi đó tốc độ của xe không đổi.
Câu 19:
Một ca nô đi trên mặt nước yên lặng với vận tốc có độ lớn là 16 m/s, vận tốc của dòng nước có độ lớn là 2 m/s. Góc giữa vectơ vận tốc của ca nô và vectơ vận tốc của dòng nước là α (0 < α < 180o). Độ lớn vận tốc tổng hợp của ca nô có thể là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vận tốc tổng hợp của ca nô lớn nhất khi α = 0 \[ \Rightarrow \] vmax = 16 + 2 = 18 m/s.
Vận tốc tổng hợp của ca nô nhỏ nhất khi α = 180° \[ \Rightarrow \] vmin = 16 – 2 = 14 m/s.
Do vậy khi 0 < α < 180° thì 14 m/s < v < 18 m/s.
\[ \Rightarrow \] v = 16 m/s là giá trị có thể có của độ lớn vận tốc tổng hợp của cano.
Câu 20:
Độ dốc của đồ thị vận tốc – thời gian cho chúng ta biết đại lượng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Độ dốc của đồ thị vận tốc – thời gian cho chúng ta biết đại lượng gia tốc.
Câu 21:
Diện tích khu vực dưới đồ thị vận tốc – thời gian cho chúng ta biết đại lượng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Diện tích khu vực dưới đồ thị vận tốc – thời gian cho chúng ta biết đại lượng độ dịch chuyển.
Câu 22:
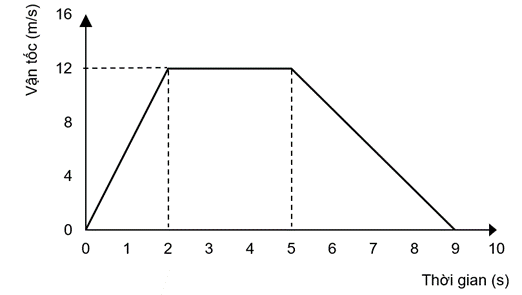
Hình dưới là đồ thị vận tốc - thời gian của một chiếc xe chuyển động thẳng. Trường hợp nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
A – Trong khoảng thời gian từ 2s đến 5 s xe chuyển động với vận tốc không đổi là 12 m/s.
B – Tại thời điểm t = 9 s, vận tốc của xe là 0 m/s.
C – Trong 4 s cuối, gia tốc của xe là: \[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 12}}{{9 - 5}} = - \frac{{12}}{4} = - 3{\rm{ m/}}{{\rm{s}}^2}\]
Có nghĩa là, trong 4 s cuối vận tốc của xe giảm dần, gia tốc của xe lúc đó có độ lớn là 3 m/s2.
D. Trong 2 s đầu, gia tốc của xe là: \[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{12 - 0}}{{2 - 0}} = \frac{{12}}{2} = 6{\rm{ m/}}{{\rm{s}}^2}\].
Câu 23:
Từ trạng thái đứng yên, một vật chuyển động với gia tốc 4 m/s2 trong 3 s. Vận tốc của vật sau 3 s là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_2} - {v_1}}}{{\Delta t}} \Rightarrow {v_2} = a.\Delta t + {v_1}\]
Vận tốc ban đầu của vật là v1 = 0 m/s
Vậy vận tốc của vật sau 3 s là: \[{v_2} = a.\Delta t + {v_1} = 4.3 + 0 = 12{\rm{ m/s}}\].
Câu 24:
Một chiếc xe đang chạy trên đường thẳng thì tài xế tăng tốc độ với gia tốc bằng 2 m/s2 trong khoảng thời gian 10 s. Độ thay đổi vận tốc trong khoảng thời gian này là?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[a = \frac{{\Delta v}}{{\Delta t}} \Rightarrow \Delta v = a.\Delta t = 2.10 = 20{\rm{ m/s}}\]
Vậy độ thay đổi vận tốc trong khoảng thời gian này là 20 m/s.
Câu 25:
Phát biểu nào dưới đây là sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Trong chuyển động thẳng biến đổi đều, quãng đường được xác định là: \[s = {v_0}t + \frac{1}{2}a{t^2}\]. Do đó, ngoài thời gian, quãng đường đi được còn phụ thuộc vào vận tốc ban đầu và độ lớn gia tốc của vật.
Câu 26:
Khi ô tô đang chạy với vận tốc 10 m/s trên đoạn đường thẳng thì người lái xe tăng ga. Sau 20 s, ô tô đạt vận tốc 14 m/s. Gia tốc a và vận tốc v của ô tô sau 40 s kể từ lúc bắt đầu tăng ga là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gia tốc của ô tô là: \[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{14 - 10}}{{20}} = \frac{4}{{20}} = 0,2{\rm{ m/}}{{\rm{s}}^2}\]
Vận tốc của ô tô sau 40 s kể từ lúc bắt đầu tăng ga là:
v = v0 + a.t = 10 + 0,2.40 = 18 m/s.
Câu 27:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nhiều thì nghiệm do các nhà khoa học tiến hành đã cho thấy gia tốc của một vật rơi tự do trên bề mặt Trái Đất, gia tốc \[\overrightarrow g \] có giá trị phụ thuộc vào vị trí mà vật rơi. Nên nếu các vật rơi ở cùng 1 vị trí, chúng sẽ có gia tốc như nhau.
Câu 28:
Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25 m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,5 m (theo phương ngang)? Lấy g = 10 m/s2. Vận tốc của viên bi khi nó bắt đầu rời khỏi mép bàn là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Chuyển động của hòn bi coi như là một chuyển động ném ngang với độ cao ban đầu h = 1,25 m và có tầm xa theo phương ngang L = 1,5 m.
Theo phương thẳng đứng, viên bi rơi tự do với vận tốc ban đầu theo phương thẳng đứng là 0. Thời gian hòn bi rơi hết độ cao 1,25 m là: \[t = \sqrt {\frac{{2h}}{g}} = 0,5{\rm{ s}}\].
Tầm xa: \[L = {v_o}.t \Rightarrow {v_o} = \frac{L}{t} = \frac{{1,5}}{{0,5}} = 3\,m/s\]
Câu 29:
Một chiếc thuyền đi xuôi dòng 1,6 km rồi quay đầu đi ngược dòng 1,2 km. Toàn bộ chuyến đi mất 45 phút. Tìm:
Tốc độ trung bình của thuyền.
 Xem đáp án
Xem đáp án
Đổi 45 phút = 0,75 h
Quãng đường đi được: \[s = 1,6 + 1,2 = 2,8\,km\]
Tốc độ trung bình của thuyền: \[{v_{tb}} = \frac{s}{t} = \frac{{2,8}}{{0,75}} = 3,7\,km/h\]
Câu 30:
Một chiếc thuyền đi xuôi dòng 1,6 km rồi quay đầu đi ngược dòng 1,2 km. Toàn bộ chuyến đi mất 45 phút. Tìm:
Độ dịch chuyển của thuyền.
 Xem đáp án
Xem đáp án
Đổi 45 phút = 0,75 h
Chọn chiều dương là chiều chuyển động ban đầu (lúc xuôi dòng).
Độ dịch chuyển: \[d = 1,6 - 1,2 = 0,4\,km\] hướng xuôi dòng
Câu 31:
Một chiếc thuyền đi xuôi dòng 1,6 km rồi quay đầu đi ngược dòng 1,2 km. Toàn bộ chuyến đi mất 45 phút. Tìm:
Vận tốc trung bình của thuyền.
 Xem đáp án
Xem đáp án
Đổi 45 phút = 0,75 h
Vận tốc trung bình: \[v = \frac{d}{t} = \frac{{0,4}}{{0,75}} = 0,53\,km/h\] hướng xuôi dòng.
Câu 32:
Một vận động viên ném một quả bóng theo phương thẳng đứng lên trên với tốc độ ban đầu là 18,0 m/s.
Quả bóng lên cao bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn trục tọa độ có phương thẳng đứng.
Chiều dương là chiều chuyển động của quả bóng khi được ném lên trên.
Gốc tọa độ tại vị trí ném.
Khi quả bóng lên đến độ cao cực đại thì vận tốc tại đó bằng 0.
Gia tốc trọng trường có phương thẳng đứng, chiều dương hướng xuống (ngược chiều chuyển động của quả bóng khi ném lên).
\[{v^2} - v_0^2 = 2as \Leftrightarrow 0 - {18^2} = 2.\left( { - 9,8} \right).s \Leftrightarrow s = 16,5\,m\]
Câu 33:
Một vận động viên ném một quả bóng theo phương thẳng đứng lên trên với tốc độ ban đầu là 18,0 m/s.
Sau thời gian bao lâu nó trở về điểm ném?
 Xem đáp án
Xem đáp án
Chọn trục tọa độ có phương thẳng đứng.
Chiều dương là chiều chuyển động của quả bóng khi được ném lên trên.
Gốc tọa độ tại vị trí ném.
Thời gian quả bóng trở về vị trí ném ban đầu bằng 2 lần thời gian bóng rơi từ độ cao 16,5 m xuống vị trí ném (thời gian rơi bằng thời gian vật rơi tự do từ độ cao 16,5 m).
\[ \Rightarrow t = 2{t_2} = 2.\sqrt {\frac{{2s}}{g}} = 2.\sqrt {\frac{{2.16,5}}{{9,8}}} = 3,66\,s\]
Câu 34:
Đồ thị vận tốc – thời gian của một vật chuyển động dọc theo trục x được thể hiện trong hình 1.5. Xác định gia tốc trung bình của vật trong các khoảng thời gian:
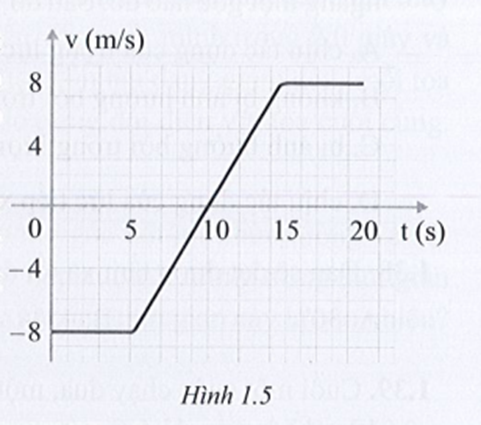
t = 5,00 s đến t = 15,0 s.
 Xem đáp án
Xem đáp án
Gia tốc trung bình trong khoảng thời gian từ t = 5,00 s đến t = 15,0 s
\[a = \frac{{8 - \left( { - 8} \right)}}{{15 - 5}} = 1,6\,m/{s^2}\]
Câu 35:
Đồ thị vận tốc – thời gian của một vật chuyển động dọc theo trục x được thể hiện trong hình 1.5. Xác định gia tốc trung bình của vật trong các khoảng thời gian:
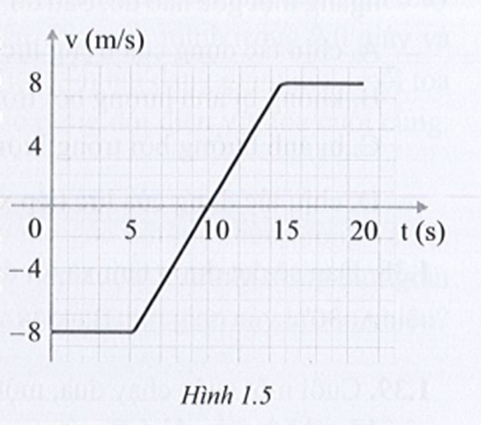
t = 0 đến t = 20,0 s.
 Xem đáp án
Xem đáp án
Gia tốc trung bình trong khoảng thời gian từ t = 0 s đến t = 20,0 s
\[a = \frac{{8 - \left( 8 \right)}}{{20 - 0}} = 0,8\,m/{s^2}\]
