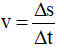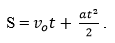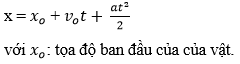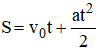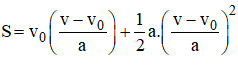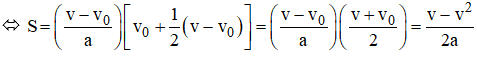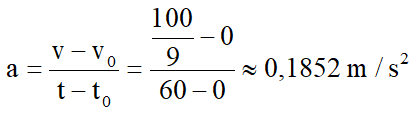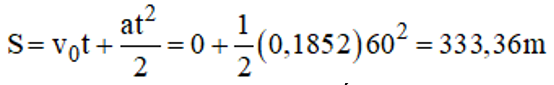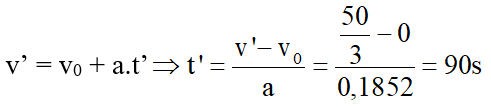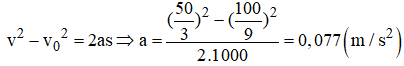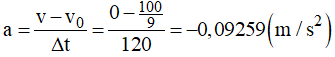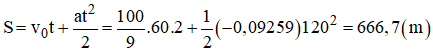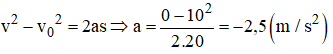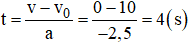15 câu hỏi trắc nghiệm thuộc Bài 3: Chuyển động thẳng biến đổi đều

Câu 1:

Viết công thức tính vận tốc tức thời của một vật chuyển động tại một điểm trên quỹ đạo. Cho biết yêu cầu về độ lớn của các đại lượng trong công thức đó.

Xem đáp án

Công thức tính vận tốc tức thời:

Với Δs: Độ dời vật thực hiện được trong thời gian rất ngắn Δt

Câu 2:

Vectơ vận tốc tức thời tại một điểm của một chuyển động thẳng được xác định:

Xem đáp án

- Điểm đặt: đặt vào vật chuyển động

- Hướng: là hướng của chuyển động

- Độ dài: tỉ lệ với độ lớn của vận tốc tức thời theo một tỉ lệ xích quy ước.

Câu 3:

Chuyển động thẳng nhanh dần đều, chậm dần đều là gì?

Xem đáp án

+ Chuyển động thẳng nhanh dần đều là chuyển động thẳng có độ lớn của vận tốc tức thời tăng dần theo thời gian.

+ Chuyển động thẳng chậm dần đều là chuyển động thẳng có độ lớn của vận tốc tức thời giảm dần theo thời gian.

Câu 4:

Viết công thức tính vận tốc của chuyển động thẳng nhanh, chậm dần đều. Nói rõ dấu của các loại đại lượng tham gia vào công thức đó.

Xem đáp án

Công thức tính vận tốc: v = v_o + at.

+ Nếu chuyển động cùng chiều với chiều dương của trục tọa độ đã chọn thì v₀ > 0.

+ Chuyển động là nhanh dần đều thì dấu a cùng dấu v₀ ngược lại, nếu chuyển động là chậm dần đều thì dấu a trái dấu v₀.

Câu 5:

Gia tốc của chuyển động thẳng nhanh, chậm dần đều có đặc điểm gì? Gia tốc được đo bằng đơn vị nào? Chiều của vectơ gia tốc của các chuyển động này có đặc điểm gì?

Xem đáp án

+ Gia tốc của chuyển động thẳng nhanh, chậm dần đều cho biết vận tốc biến thiên nhanh hay chậm theo thời gian. Gia tốc là đại lượng vectơ có điểm đặt, phương, chiều và độ lớn.

+ Gia tốc được đo bằng đơn vị: m/s².

+ Đặc điểm của chiều của vectơ gia tốc:

a.v > 0 ⇒ Chuyển động thẳng nhanh dần đều. Vectơ a cùng phương, cùng chiều với vectơ v

a.v < 0 ⇒ Chuyển động thẳng chậm dần đều. Vectơ a cùng phương, ngược chiều với vectơ v

Câu 6:

Viết công thức tính quãng đường đi được của chuyển động thẳng nhanh, chậm dần đều. Nói rõ dấu của các đại lượng tham gia vào công thức đó. Quãng đường đi được trong các chuyển động này phụ thuộc vào thời gian theo hàm số dạng gì?

Xem đáp án

Công thức tính quãng đường đi:

+ Chuyển động theo chiều (+) thì v_o > 0.

+ Nhanh dần đều: a.v > 0 tức a cùng dấu với v_o và v.

+ Chậm dần đều: a.v < 0 tức a trái dấu với v_o và v.

Nhận xét: Quãng đường đi được trong các chuyển động thẳng biến đổi đều phụ thuộc vào thời gian theo hàm số bậc hai.

Câu 7:

Viết phương trình chuyển động của chuyển động thẳng nhanh, chậm dần đều.

Xem đáp án

Phương trình chuyển động của chuyển động thẳng nhanh, chậm dần đều:

Câu 8:

Thiết lập công thức tính gia tốc của chuyển động thẳng biến đổi đều theo vận tốc và quãng đường đi được.

Xem đáp án

Từ công thức v = v₀ + at => $t = \frac{v - v_{0}}{a}$ thế vào công thức:

$S = v_{0} t + \frac{{at}^{2}}{2}$ ta được:

$S = v_{0} (\frac{v - v_{0}}{a}) + \frac{1}{2} a {(\frac{v - v_{0}}{a})}^{2} \Leftrightarrow S = (\frac{v - v_{0}}{a}) [v_{0} + \frac{1}{2} (v - v_{0})] = (\frac{v - v_{0}}{a}) (\frac{v + v_{0}}{a}) = \frac{v^{2} + v_{0}^{2}}{a} \Leftrightarrow v^{2} + v_{0}^{2} = 2 aS \Rightarrow a = \frac{v^{2} + v_{0}^{2}}{2 S}$

Câu 9:

Câu nào đúng?

A. Gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều

B. Chuyển động thẳng nhanh dần đều có gia tốc lớn thì có vận tốc lớn

C. Chuyển động thẳng biến đổi đều có gia tốc tăng, giảm đều theo thời gian

D. Gia tốc trong chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi

Xem đáp án

Chọn D.

A, B sai vì tính chất nhanh dần chậm dần của chuyển động thẳng biến đổi đều chỉ xác định dựa vào dấu của tích a.v tại thời điểm mà ta xét. Do vậy ta không thể khẳng định được gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều hoặc chuyển động thẳng nhanh dần đều có gia tốc lớn thì có vận tốc lớn.

C sai vì chuyển động thẳng biến đổi đều có vận tốc tăng, giảm đều theo thời gian (tức gia tốc a không thay đổi về độ lớn)

D đúng vì trong chuyển động thẳng nhanh dần đều a.v > 0 nên phương và chiều của a cùng phương, cùng chiều với v, phương và chiều của v là phương và chiều của chuyển động.

Câu 10:

Trong công thức tính vận tốc của chuyển động thẳng nhanh dần đều v = v_o + at thì

A. v luôn luôn dương

B. a luôn luôn dương

C. a luôn luôn cùng dấu với v

D. a luôn luôn ngược dấu với v

Xem đáp án

Chọn C.

a luôn luôn cùng chiều với v tức a.v > 0. Trong chậm dần đều a.v < 0.

Câu 11:

Công thức nào dưới đây là công thức liên hệ giữa vận tốc, gia tốc và quãng đường đi được của chuyển động thẳng nhanh dần đều?

A. $v + v_{0} = \sqrt{2 a s}$

B. $v^{2} + v_{0}^{2} = 2 a s$

C. $v - v_{0} = \sqrt{2 a s}$

D. $v^{2} - v_{0}^{2} = 2 a s$

Xem đáp án

Chọn D.

Từ công thức v = v_o + at

thế vào công thức:

Ta được:

Câu 12:

Một đoàn tàu rời ga chuyển động thẳng nhanh dần đều. Sau 1 phút tàu đạt tốc độ 40 km/h.

a) Tính gia tốc của đoàn tàu.

b) Tính quãng đường mà tàu đi được trong 1 phút.

c) Nếu tiếp tục tăng tốc như vậy thì sau bao lâu nữa tàu sẽ đạt tốc độ 60 km/h.

Xem đáp án

a) Đổi v = 40 km/h = 100/9 m/s, t = 1 phút = 60s.

Ban đầu t₀ = 0 thì v₀ = 0.

Gia tốc của đoàn tàu là:

b) Quãng đường tàu đi được trong thời gian t = 1 phút = 60 s là:

c) Gọi t’ là thời gian tàu đạt tốc độ v’ = 60 km/h = 50/3 m/s kể từ lúc ban đầu t₀ = 0.

Ta có:

Như vậy nếu tính từ lúc đạt tốc độ v = 40 km/h thì sau khoảng thời gian ∆t = t’ – t = 90 – 60 = 30 s thì xe đạt tốc độ v’ = 60 km/h.

Câu 13:

Một ô tô đang chạy thẳng đều với tốc độ 40 km/h bỗng tăng ga chuyển động nhanh dần đều. Tính gia tốc của xe, biết rằng sau khi chạy được quãng đường 1 km thì ô tô đạt tốc độ 60 km/h.

Xem đáp án

Ta có: v_o = 40 km/h = 100/9 m/s; s = 1 km = 1000 m; v = 60 km/h = 50/3 m/s

Áp dụng công thức liên hệ gia tốc, vận tốc và quãng đường.

Ta có gia tốc của xe được tính bằng công thức:

Câu 14:

Một đoàn tàu đang chạy với tốc độ 40 km/h thì hãm phanh, chuyển động thẳng chậm dần đều để vào ga. Sau 2 phút thì tàu dừng lại ở sân ga.

a) Tính gia tốc của đoàn tàu.

b) Tính quãng đường mà tàu đi được trong thời gian hãm phanh.

Xem đáp án

Ta có: Ban đầu v₀ = 40 km/h = 100/9 m/s.

Sau đó Δt = 2 phút = 120 s thì tàu dừng lại: v = 0

a) Gia tốc của đoàn tàu là:

b) Quãng đường mà tàu đi đi được trong thời gian hãm phanh là:

Câu 15:

Một xe máy đang đi với tốc độ 36 km/h bỗng người lái xe thấy có một cái hố trước mặt, cách xe 20 m. Người ấy phanh gấp và xe đến sát miệng hố thì dừng lại.

a) Tính gia tốc của xe.

b) Tính thời gian hãm phanh.

Xem đáp án

Ta có: ban đầu xe có v₀ = 36 km/h = 10 m/s

Sau đó xe hãm phanh, sau quãng đường S = 20 m xe dừng lại: v = 0

a) Gia tốc của xe là:

b) Thời gian hãm phanh là:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Vật lý 10 Chương 1: Động học chất điểm

Bài 3: Chuyển động thẳng biến đổi đều

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương