Giải bài tập Toán 10 Bài tập cuối chương 5

A. Trắc nghiệm

Bài 5.17 trang 89 Toán 10 Tập 1: Khi cân một bao gạo bằng một cân treo với thang chia 0,2 kg thì độ chính xác d là:

A. 0,1 kg.

B. 0,2kg.

C. 0,3 kg.

D. 0,4kg.

Lời giải:

Cân một bao gạo bằng một cân treo với thang chia 0,2 kg.

Mà trong các phép đo, độ chính xác d của số gần đúng bằng một nửa đơn vị của thước đo.
Khi đó d = 0,1 kg.

Chọn A.

Bài 5.18 trang 89 Toán 10 Tập 1: Trong hai mẫu số liệu, mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn là đúng hay sai?

A. Đúng.

B. Sai.

Lời giải:

Ta có độ lệch chuẩn bằng căn bậc hai của phương sai.

Do đó, mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn.

Chọn A.

Bài 5.19 trang 89 Toán 10 Tập 1: Có 25% giá trị của mẫu số liệu nằm giữa Q₁ và Q₃, đúng hay sai?

A. Đúng.

B. Sai.

Lời giải:

Ta có giá trị Q₂ chia mẫu số liệu thành hai phần bằng nhau.

+ Xét nửa số liệu bên trái: giữa Q₁ và Q₂ là nửa của nửa số liệu bên trái.

+ Xét nửa số liệu bên phải: giữa Q₃ và Q₂ là nửa của nửa số liệu bên phải.

Do đó có 50% giá trị của số liệu nằm nữa hai giá trị Q₁ và Q₃.

Vì vậy phát biểu đã cho là sai.

Chọn B.

Bài 5.20 trang 89 Toán 10 Tập 1: Số đặc trưng nào sau đây đo độ phân tán của mẫu số liệu?

A. Số trung bình.

B. Mốt.

C. Trung vị.

D. Độ lệch chuẩn.

Lời giải:

Độ lệch chuẩn đặc trưng cho độ phân tán của mẫu số liệu.

Số trung bình, mốt, trung vị đo xu thế trung tâm của mẫu số liệu.

Chọn D.

Bài 5.21 trang 89 Toán 10 Tập 1: Điểm trung bình môn học kì I một số môn học của An là: 8; 9; 7; 6; 5; 7; 3. Nếu An được cộng thêm mỗi môn 0,5 điểm chuyên cần thì các số đặc trưng nào sau đây của mẫu số liệu không thay đổi?

A. Số trung bình.

B. Trung vị.

C. Độ lệch chuẩn.

D. Tứ phân vị.

Lời giải:

Nếu An được cộng thêm mỗi môn 0,5 điểm chuyên cần, tức là mỗi số trong dãy số liệu trên đều tăng 0,5.

Do đó, trung vị tăng 0,5 và tứ phân vị cũng tăng 0,5.

Khi cộng thêm mỗi môn 0,5 điểm chuyên cần, tức là tổng điểm 7 môn đó tăng 3,5 điểm.

Ta lấy phần tăng đó chia đều cho 7 thì điểm trung bình tăng 0,5.

Nên độ lệch của mỗi giá trị so với số trung bình vẫn không đổi $|x_i-\overline{x}|$.

Do đó độ lệch chuẩn không thay đổi.

Chọn C

B. Tự luận

Bài 5.22 trang 89 Toán 10 Tập 1: Lương khởi điểm của 5 sinh viên vừa tốt nghiệp tại một trường đại học (đơn vị triệu đồng) là:

3,5     9,2     9,2     9,5     10,5.

a) Giải thích tại sao nên dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này.

b) Nên dùng khoảng biến thiên hay khoảng tứ phân vị để đo độ phân tán? Vì sao?

Lời giải

a) Trong 5 sinh viên trên, có một sinh viên có mức lương rất thấp so với các sinh viên còn lại (3,5 triệu đồng, thấp hơn rất nhiều so với các giá trị còn lại trong dãy số liệu). Vì vậy, nên dùng trung vị để đo mức lương sau khi tốt nghiệp.

b) Nên dùng khoảng tứ phân vị để đo độ phân tán vì độ phân tán không bị ảnh hưởng bởi giá trị bất thường.

Bài 5.23 trang 89 Toán 10 Tập 1: Điểm Toán và Tiếng Anh của 11 học sinh lớp 10 được cho trong bảng sau:

Hãy so sánh mức độ học đều của học sinh môn Tiếng Anh và môn Toán thông qua các số đặc trưng: khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn.

Lời giải

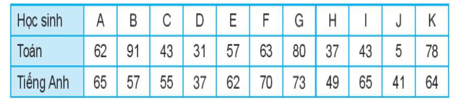
∙ Môn Toán:

Điểm môn Toán của 11 bạn học sinh lớp 10 xếp theo thứ tự không giảm là:

5; 31; 37; 43; 43; 57; 62; 63; 78; 80; 91.

Số trung bình cộng điểm Toán:

$\overline{X}=\frac{5+31+37+43+43+57+62+63+78+80+91}{11}\approx 53,64.$

Ta có giá trị lớn nhất của mẫu số liệu là 91 và giá trị nhỏ nhất là 5. Khi đó, khoảng biến thiên là: R = 91 – 5 = 86.

Vì n = 11 là số lẻ nên trung vị Q₂ = 57.

Nửa bên trái trung vị có 5 giá trị nên tứ phân vị thứ nhất Q₁ = 37.

Nửa bên phải trung vị có 5 giá trị nên tứ phân vị thứ ba Q₃ = 78.

Suy ra khoảng tứ phân vị là: Δ_Q = Q₃ – Q₁ = 78 – 37 = 41.

Ta có bảng sau:

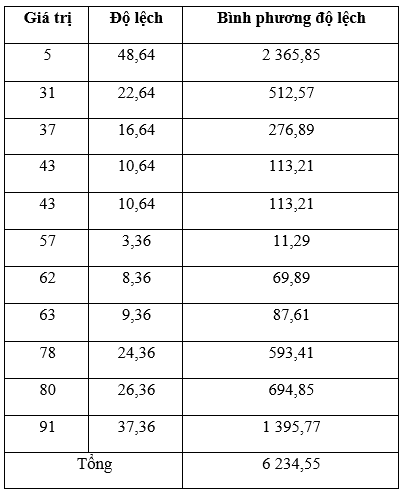
Phương sai: $s^2\approx \frac{6234,55}{11}\approx 566,78$.

Độ lệch chuẩn: $s=\sqrt{s^2}\approx \sqrt{566,78}\approx 23,81$.

∙ Môn Tiếng Anh:

Điểm môn Tiếng Anh của 11 bạn học sinh lớp 10 xếp theo thứ tự không giảm là:

37; 41; 49; 55; 57; 62; 64; 65; 65; 70; 73.

Số trung bình cộng điểm Tiếng Anh:

$\overline{X^{\text{'}}}=\frac{37+41+49+55+57+62+64+65+65+70+73}{11}=58.$

Ta có giá trị lớn nhất của mẫu số liệu là 73 và giá trị nhỏ nhất là 37. Khi đó khoảng biến thiên là: R' = 73 – 37 = 36.

Vì n = 11 là số lẻ nên trung vị Q'₂ = 62.

Nửa bên trái trung vị có 5 giá trị nên tứ phân vị thứ nhất Q'₁ = 49.

Nửa bên phải trung vị có 5 giá trị nên tứ phân vị thứ ba Q'₃ = 65.

Suy ra khoảng tứ phân vị là: Δ'_Q = Q'₃ – Q'₁ = 65 – 49 = 16.

Ta có bảng sau:

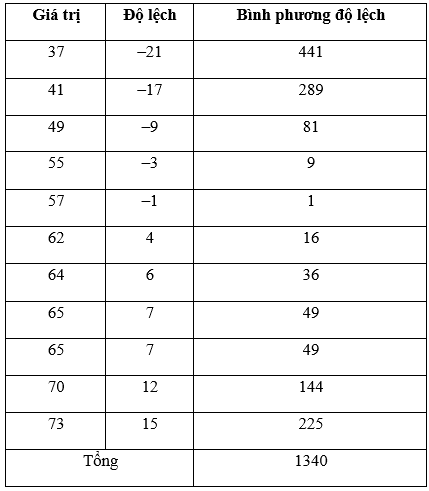
Phương sai: ${s^{\text{'}}}^2=\frac{1340}{11}\approx 121,81$.

Độ lệch chuẩn: $s^{\text{'}}=\sqrt{{s^{\text{'}}}^2}\approx \sqrt{121,81}\approx 11,04$.

Nhận xét:

∙ Vì 23,81 > 11,04 nên độ lệch chuẩn của mẫu số liệu điểm môn Toán lớn hơn môn Tiếng Anh.

Do đó, độ phân tán của số liệu điểm môn Toán cao hơn môn Tiếng Anh hay 11 bạn học sinh lớp 10 này học đều môn Tiếng Anh hơn môn Toán.

∙ Vì 86 > 36 nên khoảng biến thiên của mẫu số liệu điểm môn Toán lớn hơn môn Tiếng Anh.

Do đó, độ phân tán của số liệu điểm môn Toán cao hơn môn Tiếng Anh hay 11 bạn học sinh lớp 10 này học đều môn Tiếng Anh hơn môn Toán.

∙ Vì 41 > 16 nên khoảng tứ phân vị của mẫu số liệu điểm môn Toán lớn hơn môn Tiếng Anh.

Do đó, độ phân tán của số liệu điểm Toán cao hơn môn Tiếng Anh hay 11 bạn học sinh lớp 10 này học đều môn Tiếng Anh hơn môn Toán.

Bài 5.24 trang 90 Toán 10 Tập 1: Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người).

a) Tìm số trung bình và trung vị của mẫu số liệu trên.

b) Giải thích tại sao số trung bình và trung vị lại có sự sai khác nhiều.

c) Nên sử dụng số trung bình hay trung vị đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ?

Lời giải:

Ta thấy có tất cả 11 tỉnh thành nên n = 11.

Số trung bình của dãy số liệu trên là:

$\frac{7,52+1,09+1,25+1,27+1,81+2,01+1,19+1,79+0,81+1,85+0,97}{11}=1,96$

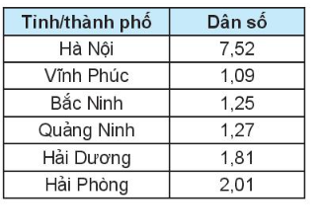
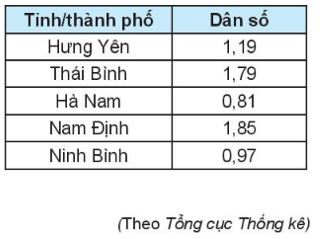
Sắp xếp dãy số liệu trên theo thứ tự không giảm, ta được:

0,81; 0,97; 1,09; 1,19; 1,25; 1,27; 1,79, 1,81; 1,85; 2,01; 7,52.

Vì n = 11 là một số lẻ nên trung vị là số chính giữa là: Q₂ = 1,27.

b) Ta thấy 7,52 lệch hẳn so với các số liệu còn lại trong dãy số liệu nên đây là giá trị bất thường của mẫu số liệu. Mà số trung bình thì ảnh hưởng bởi giá trị bất thường.

Do đó, số trung bình và trung vị có sự sai khác nhiều.

c) Do có giá trị 7,52 là giá trị khác biệt so với các giá trị còn lại nên gây ảnh hưởng đến số trung bình.

Do đó, ta nên sử dụng số trung vị để đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc Bộ.

Bài 5.25 trang 90 Toán 10 Tập 1: Hai mẫu số liệu sau đây cho biết số lượng trường Trung học phổ thông ở mỗi tỉnh/thành phố thuộc Đồng bằng sông Hồng và Đồng bằng sông Cửu Long năm 2017:

Đồng bằng sông Hồng: 187  34   35   46   54    57   37   39   23   57   27.

Đồng bằng sông Cửu Long: 33   34   33   29   24   39   42   24   23   19   24   15   26.

(Theo Tổng cục Thống kê)

a) Tính số trung bình, trung vị, các tứ phân vị, mốt, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn cho mỗi mẫu số liệu trên.

b) Tại sao số trung bình của hai mẫu số liệu có sự sai khác nhiều trong khi trung vị thì không?

c) Tại sao khoảng biến thiên và độ lệch chuẩn của hai mẫu số liệu khác nhau nhiều trong khi khoảng tứ phân vị thì không?

Lời giải

a)

∙ Đồng bằng sông Hồng: 187  34  35   46   54   57   37   39   23   57   27.

Ta có: n = 11.

Số trung bình: 

$\overline{X}=\frac{187 +34 +35 +46 +54 +57 +37 +39 +23 +57 +27}{11}\approx 54,18.$

Sắp xếp số liệu trên theo thứ tự không giảm ta được:

23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.

Vì n = 11 là số lẻ nên trung vị Q₂ = 39.

Nửa số liệu bên trái có 5 giá trị nên tứ phân vị thứ nhất là: Q₁ = 34.

Nửa số liệu bên phải có 5 giá trị nên tứ phân vị thứ ba là: Q₃ = 57.

Khoảng tứ phân vị là:

Δ_Q = Q₃ – Q₁ = 57 – 34 = 23.

Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.

Theo quan sát số liệu, ta thấy giá trị 57 có tần số xuất hiện nhiều nhất nên mốt là 57.

Ta có bảng sau:

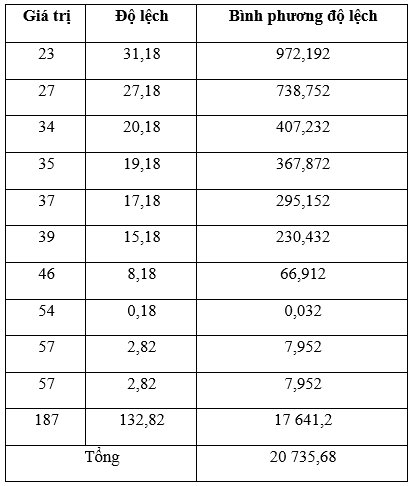
Phương sai: $s^2\approx \frac{20735,68}{11}\approx 1885,06$

Độ lệch chuẩn: $s=\sqrt{s^2}\approx \sqrt{1885,06}\approx 43,42$

∙ Đồng bằng sông Cửu Long: 33   34   33   29   24   39   42   24   23   19   24   15   26.

Số trung bình của mẫu số liệu:

$\overline{X^{\text{'}}}=\frac{33 +34 +33 +29 +24 +39 +42 +24 +23 +19 +24 +15 +26}{13}\approx 28,08.$ 

Sắp xếp số liệu trên theo thứ tự không giảm ta được:

15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.

Vì n' = 13 là số lẻ nên trung vị Q'₂ = 26.

Nửa số liệu bên trái có 6 giá trị nên tứ phân vị thứ nhất là: Q'₁ = (23 + 24):2 = 23,5.

Nửa số liệu bên phải có 6 giá trị nên tứ phân vị thứ ba là: Q'₃ = (33 + 34):2 = 33,5.

Khoảng tứ phân vị là:

Δ'_Q = Q'₃ – Q'₁ = 33,5 – 23,5 = 10.

Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R' = 42 – 15 = 27.

Theo quan sát số liệu, ta thấy giá trị 24 có tần số xuất hiện nhiều nhất nên mốt là 24.

Ta có bảng sau:

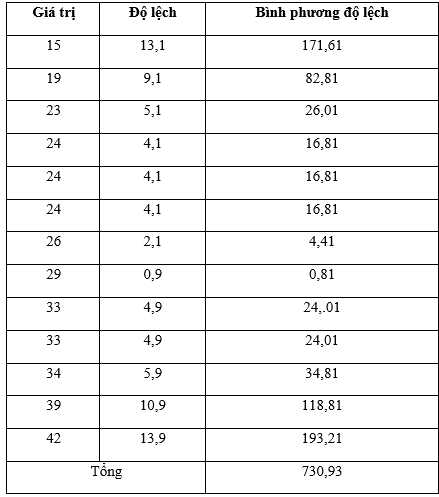
Phương sai: ${s^{\text{'}}}^2\approx$$\frac{730,93}{13}\approx 56,23$.

Độ lệch chuẩn: $s^{\text{'}}=\sqrt{{s^{\text{'}}}^2}\approx$$\sqrt{56,23}\approx 7,5$

b) Số trung bình sai khác vì ở Đồng bằng sông Hồng thì có giá trị bất thường là 187 (cao hơn hẳn so với các giá trị còn lại), còn ở Đồng bằng sông Cửu Long thì không có giá trị bất thường.

Chính giá trị bất thường làm nên sự sai khác đó, còn trung vị không bị ảnh hưởng đến giá trị bất thường nên trung vị ở hai mẫu số liệu không khác nhau quá nhiều.

c) Giá trị bất thường ảnh hưởng đến khoảng biến thiên và độ lệch chuẩn, còn với khoảng tứ phân vị thì không (khoảng tứ phân vị đo 50% giá trị ở chính giữa).

Bài 5.26 trang 90 Toán 10 Tập 1: Tỉ lệ trẻ em suy dinh dưỡng (tính theo cân nặng tương ứng với độ tuổi) của 10 tỉnh thuộc Đồng bằng sông Hồng được cho như sau:

5,5   13,8   10,2   12,2   11,0   7,4   11,4   13,1    12,5   13,4.

(Theo Tổng cục Thống kê)

a) Tính số trung bình, trung vị, khoảng biến thiên và độ lệch chuẩn của mẫu số liệu trên.

b) Thực hiện làm tròn đến hàng đơn vị cho các giá trị trong mẫu số liệu. Sai số tuyệt đối của phép làm tròn này không vượt quá bao nhiêu?

Lời giải:

a) Số trung bình của mẫu số liệu là:

$\overline{X}=\frac{5,5 +13,8 +10,2 +12,2 +11,0 +7,4 +11,4+13,1 +12,5 +13,4}{10}=11,05$

Sắp xếp dãy số liệu theo thứ tự không giảm, ta được:

5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13,8.

Vì n = 10 là số chẵn nên số trung vị là trung bình cộng của hai giá trị chính giữa:

(11,4 + 12,2) : 2 = 11,8.

Ta có giá trị lớn nhất của số liệu là 13,8 và giá trị nhỏ nhất là 5,5.

Khi đó khoảng biến thiên là: R = 13,8 – 5,5 = 8,3.

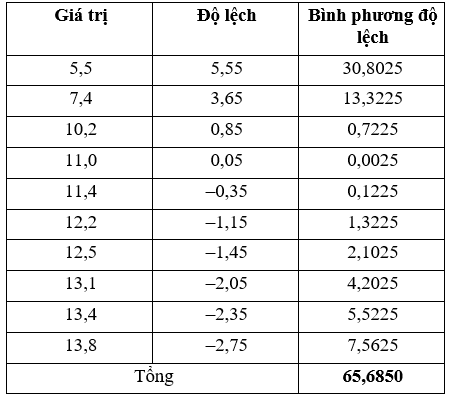
Phương sai: $s^2\approx \frac{65,6850}{10}\approx 6,57$

Độ lệch chuẩn: $s=\sqrt{s^2}\approx \sqrt{6,57}\approx 2,56$

Vậy số trung bình là 11,05; trung vị là 11, 8; khoảng biến thiên là 8,3 và độ lệch chuẩn là 2,56.

b) Thực hiện làm tròn đến hàng đơn vị cho các giá trị trong mẫu số liệu:

5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13,8.

Ta được:

6 ; 7; 10; 11; 11; 12; 13; 13; 13; 14.

Làm trò các số liệu trong mẫu:

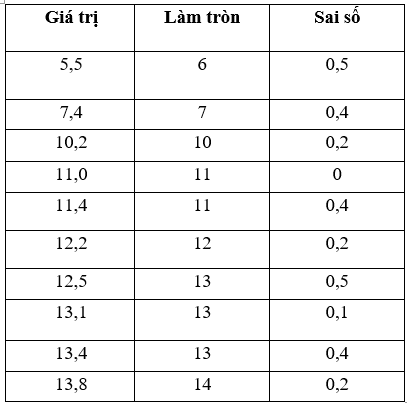
Sai số tuyệt đối của phép làm tròn này không vượt quá 0,5.