Giải bài tập Toán 10 Bài 25: Nhị thức Newton

A. Các câu hỏi trong bài

Mở đầu trang 72 Toán 10 Tập 2: Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển:

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)ⁿ khi n ∈ {4; 5} không?

Lời giải

Ta có:

a² + 2ab + b² = a² . b⁰ + 2 . a¹ . b¹ + b² . a⁰ 

a³ + 3a²b + 3ab² + b³ = a³ . b⁰ + 3 . a² . b¹ + 3 . a¹ . b² + a⁰ . b³

Quan sát vế phải của các đẳng thức, ta thấy đây là một tổng các đơn thức hai biến, bậc 2 và bậc 3, và số mũ của a được sắp xếp theo thứ tự giảm dần, còn số mũ của b theo thứ tự tăng dần.

Sau khi học bài Nhị thức Newton này, ta có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)ⁿ khi n ∈ {4; 5}.

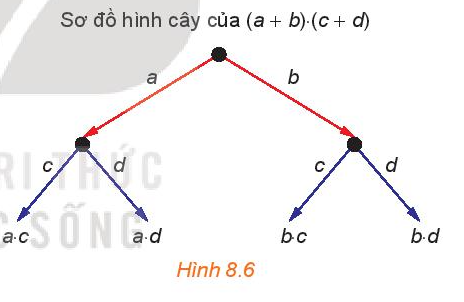
Hoạt động 1 trang 72 Toán 10 Tập 2: Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau:

• Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);

• Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;

• Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.

Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a + b) . (c + d).

Lời giải

Tổng các tích nhận được từ sơ đồ hình cây là: a.c + a.d + b.c + b.d.

Khai triển của tích (a + b) . (c + d) = a . (c + d) + b . (c + d) = a.c + a.d + b.c + b.d.

Vậy tổng của các tích nhận được từ sơ đồ hình cây trùng với kết quả của khai triển (a + b) . (c + d).

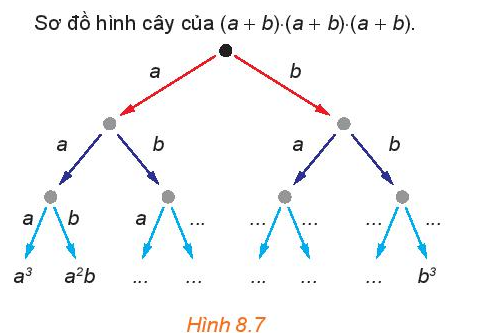
Hoạt động 2 trang 72 Toán 10 Tập 2: Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b).

Có bao nhiêu tích nhận được lần lượt bằng a³, a²b, ab², b³?

Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)³.

Lời giải

Theo quy tắc xây dựng sơ đồ hình cây như HĐ1, ta điền được các biểu thức trong sơ đồ hình cây của tích (a + b) . (a + b) . (a + b) như hình sau:

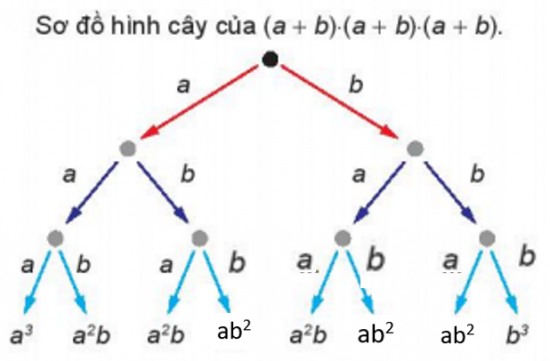
Từ đó, ta có:

- có 1 đơn thức bằng a³;

- có 3 đơn thức bằng a²b;

- có 3 đơn thức bằng ab²;

- có 1 đơn thức bằng b³.

Các hệ số nhận được: 1, 3, 3, 1.

Ở lớp 8 ta đã biết, khai triển (a + b)³ = a³ + 3a²b + 3ab² + b³.

Vậy các hệ số của khai triển trừng với các hệ số của các tích nhận được.

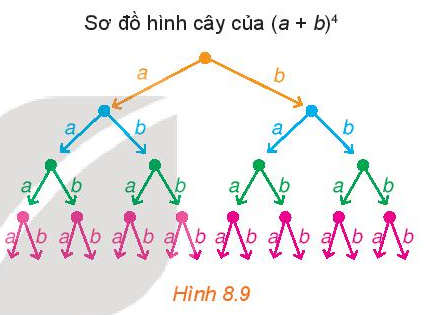
Hoạt động 3 trang 73 Toán 10 Tập 2: Sơ đồ hình cây của khai triển (a + b)⁴ được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 2⁴ (theo quy tắc nhân) đơn thức có dạng x . y . z . t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a . a . b . a, thu gọn là a³b. Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a³b trong tổng là $C_4^1$.

Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:

• a⁴; • a³b; • a²b²; • ab³; • b⁴.

Lời giải

- Để có đơn thức a⁴ thì phải có 4 nhân tử a, khi đó số đơn thức đồng dạng với a⁴ trong tổng là: $C_4^0$ = 1;

- Để có đơn thức a³b thì phải có 3 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng với a³b trong tổng là: $C_4^1$ = 4;

- Để có đơn thức a²b² thì phải có 2 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng với a²b² trong tổng là: $C_4^2$ = 6;

- Để có đơn thức ab³ thì phải có 1 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng với ab³ trong tổng là: $C_4^3$ = 4;

- Để có đơn thức b⁴ thì phải có 4 nhân tử b, khi đó số đơn thức đồng dạng với b⁴ trong tổng là: $C_4^4$ = 1.

Luyện tập 1 trang 73 Toán 10 Tập 2: Khai triển (x – 2)⁴.

Lời giải

Thay a = x và b = – 2 trong công thức khai triển của (a + b)⁴ ta được:

(x – 2)⁴ 

= x⁴ + 4x³ . (– 2) + 6x² . (–2)² + 4x . (– 2)³ + (– 2)⁴ 

= x⁴ – 8x³ + 24x² – 32x + 16.

Hoạt động 4 trang 74 Toán 10 Tập 2: Tương tự như HĐ3, sau khi khai triển (a + b)⁵, ta thu được một tổng gồm 2⁵ đơn thức có dạng x . y . z . t . u, trong đó mỗi kí hiệu x, y, z, t, u là a hoặc b. Chẳng hạn, nếu x, z là a, còn y, t, u là b thì ta có đơn thức a . b . a . b . b, thu gọn là a²b³. Để có đơn thức này, thì trong 5 nhân tử x, y, z, t, u có 3 nhân tử là b, 2 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a²b³ trong tổng là $C_5^3$.

Lập luận tương tự như trên, dùng kiến thức về tổ hợp, hãy cho biết, trong tổng nhận được nêu trên có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:

• a⁵; • a⁴b; • a³b²; • a²b³; •ab⁴; •b⁵.

Lời giải

- Để có đơn thức a⁵ thì phải có 5 nhân tử a, khi đó số đơn thức đồng dạng với a⁵ trong tổng là: $C_5^0$ = 1;

- Để có đơn thức a⁴b thì phải có 4 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng với a⁴b trong tổng là: $C_5^1$ = 5;

- Để có đơn thức a³b² thì phải có 3 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng với a³b² trong tổng là: $C_5^2$ = 10;

- Để có đơn thức a²b³ thì phải có 2 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng với a²b³ trong tổng là: $C_5^3$ = 10;

- Để có đơn thức ab⁴ thì phải có 1 nhân tử a, 4 nhân tử b, khi đó số đơn thức đồng dạng với ab⁴ là: $C_5^4$ = 5;

- Để có đơn thức b⁵ thì phải có 5 nhân tử b, khi đó số đơn thức đồng dạng với b⁵ trong tổng là: $C_5^5$ = 1.

Luyện tập 2 trang 74 Toán 10 Tập 2: Khai triển (3x – 2)⁵.

Lời giải

Thay a = 3x và b = – 2 trong công thức khai triển của (a + b)⁵ ta được:

(3x – 2)⁵ 

= (3x)⁵ + 5. (3x)⁴. (–2) + 10 . (3x)³ . (– 2)² + 10 . (3x)² . (– 2)³ + 5 . (3x) . (– 2)⁴ + (– 2)⁵

= 243x⁵ – 810x⁴ + 1080x³ – 720x² + 240x – 32.

Vận dụng trang 74 Toán 10 Tập 2:

a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,05)⁴ để tính giá trị gần đúng của 1,05⁴.

b) Dùng máy tính cầm tay tính giá trị của 1,05⁴ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Lời giải

a) Viết 1,05⁴ = (1 + 0,05)⁴.

Thay thế a = 1, b = 0,05 trong công thức khai triển (a + b)⁴ ta có:

1,05⁴ = (1 + 0,05)⁴ = 1⁴ + 4 . 1³ . 0,05 + 6 . 1² . 0,05² + 4 . 1 . 0,05³ + 0,05⁴.

1,05⁴ ≈ 1⁴ + 4 . 1³ . 0,05 = 1 + 0,2 = 1,2.

Vậy giá trị gần đúng của 1,05⁴ là 1,2.

b) Sử dụng máy tính cầm tay, ta kiểm tra được rằng: 1,05⁴ = 1,21550625.

Sai số tuyệt đối là: ∆ = |1,21550625 – 1,2| = 0,01550625.

B. Bài tập

Bài 8.12 trang 74 Toán 10 Tập 2: Khai triển các đa thức:

a) (x – 3)⁴;

b) (3x – 2y)⁴;

c) (x + 5)⁴ + (x – 5)⁴;

d) (x – 2y)⁵.

Lời giải

Áp dụng các công thức khai triển của (a + b)⁴  và (a + b)⁵.

a) (x – 3)⁴ 

= x⁴ + 4 . x³ . (–3) + 6 . x² . (–3)² + 4 . x . (–3)³ + (–3)⁴

= x⁴ – 12x³ + 54x² – 108x + 81.

b) (3x – 2y)⁴ 

= (3x)⁴ + 4 . (3x)³ . (– 2y) + 6 . (3x)² . (– 2y)² + 4 . (3x) . (– 2y)³ + (– 2y)⁴

= 81x⁴ – 216x³y + 216x²y² – 96xy³ + 16y⁴.

c) (x + 5)⁴ + (x – 5)⁴ 

= (x⁴ + 4x³ . 5 + 6x² . 5² + 4x . 5³ + 5⁴) + [x⁴ + 4x³ . (– 5) + 6x² . (– 5)² + 4x . (– 5)³ + (– 5)⁴]

= (x⁴ + x⁴) + (20x³ – 20x³) + (150x² + 150x²) + (500x – 500x) + (625 + 625)

= 2x⁴ + 300x² + 1250.

d) (x – 2y)⁵ 

= x⁵ + 5x⁴ . (– 2y) + 10x³ . (– 2y)² + 10x² . (– 2y)³ + 5x . (2y)⁴ + (– 2y)⁵

= x⁵ – 10x⁴y + 40x³y² – 80x²y³ + 80xy⁴ – 32y⁵.

Bài 8.13 trang 74 Toán 10 Tập 2: Tìm hệ số của x⁴ trong khai triển của (3x –1)⁵.

Lời giải

Số hạng chứa x⁴ là: 5 . (3x)⁴ . (– 1) = – 405x⁴.

Vậy hệ số của x⁴ trong khai triển của (3x – 1)⁵ là: – 405.

Bài 8.14 trang 74 Toán 10 Tập 2: Biểu diễn ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5$ dưới dạng $a+b\sqrt{2}$ với a, b là các số nguyên.

Lời giải

Ta có:

${\left(3+\sqrt{2}\right)}^5=3^5+{5.3}^4.\sqrt{2}+{10.3}^3.{\left(\sqrt{2}\right)}^2+{10.3}^2.{\left(\sqrt{2}\right)}^3+\mathrm{5.3.}{\left(\sqrt{2}\right)}^4+{\left(\sqrt{2}\right)}^5$$=3^5+{5.3}^4.\sqrt{2}+{10.3}^3.2+{10.3}^2\mathrm{.2.}\sqrt{2}+\mathrm{5.3.4}+4\sqrt{2}$.

${\left(3-\sqrt{2}\right)}^5=3^5+{5.3}^4.\left(-\sqrt{2}\right)+{10.3}^3.{\left(-\sqrt{2}\right)}^2+{10.3}^2.{\left(-\sqrt{2}\right)}^3+\mathrm{5.3.}{\left(-\sqrt{2}\right)}^4+{\left(-\sqrt{2}\right)}^5$$=3^5-{5.3}^4.\sqrt{2}+{10.3}^3.2-{10.3}^2\mathrm{.2.}\sqrt{2}+\mathrm{5.3.4}-4\sqrt{2}$.

Suy ra: ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5$$=2\left({5.3}^4.\sqrt{2}+{10.3}^2.2\sqrt{2}+4\sqrt{2}\right)$

$=2.589\sqrt{2}=1178\sqrt{2}$$=0+1178\sqrt{2}$.

Vậy biểu diễn ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5$ dưới dạng $a+b\sqrt{2}$ với a, b là các số nguyên ta được $0+1178\sqrt{2}$.

Bài 8.15 trang 75 Toán 10 Tập 2: a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,02)⁵ để tính giá trị gần đúng của 1,02⁵.

b) Dùng máy tính cầm tay tính giá trị của 1,02⁵ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Lời giải

a) Viết 1,02⁵ = (1 + 0,02)⁵.

Thay thế a = 1, b = 0,02 trong công thức khai triển (a + b)⁵ ta có:

1,02⁵ = (1 + 0,02)⁵ = 1⁵ + 5 . 1⁴ . (0,02) + 10 . 1³ . (0,02)² + 10 . 1² . (0,02)³ + 5 . 1 . (0,02)⁴ + (0,02)⁵

 Do đó: 1,02⁵ = (1 + 0,02)⁵  ≈ 1⁵ + 5 . 1⁴ . 0,02 = 1,1.

b) Sử dụng máy tính cầm tay, ta kiểm tra được: 1,02⁵ = 1,104080803.

Sai số tuyệt đối là: ∆ = |1,104080803 – 1,1| = 0,004080803.

Bài 8.16 trang 75 Toán 10 Tập 2: Số dân của một tỉnh ở thời điểm hiện tại là khoảng 800 nghìn người. Giả sử rằng tỉ lệ tăng dân số hằng năm của tỉnh đó là r%.

a) Viết công thức tính số dân của tỉnh đó sau 1 năm, sau 2 năm. Từ đó suy ra công thức tính số dân của tỉnh đó sau 5 năm nữa là $P=800{\left(1+\frac{r}{100}\right)}^5$ (nghìn người).

b) Với r = 1,5, dùng hai số hạng đầu trong khai triển của (1 + 0,015)⁵, hãy ước tính số dân của tỉnh đó sau 5 năm nữa (theo đơn vị nghìn người).

Lời giải

a) Để tính số dân năm sau, ta lấy số dân năm trước cộng với số dân tăng hằng năm (Số dân tăng hằng năm là r% của số dân năm trước).

Số dân của tỉnh đó sau 1 năm là: 

$P_1=800+800.r\%=800\left(1+r\%\right)=800\left(1+\frac{r}{100}\right)$ (nghìn người).

Số dân của tỉnh đó sau 2 năm là:  

$P_2=P_1+P_1.r\%$$=800\left(1+\frac{r}{100}\right)+800\left(1+\frac{r}{100}\right).\frac{r}{100}$$=800\left(1+\frac{r}{100}\right)\left(1+\frac{r}{100}\right)=800{\left(1+\frac{r}{100}\right)}^2$ (nghìn người).

Suy ra công thức tính số dân của tỉnh đó sau 5 năm nữa là: 

$P=800{\left(1+\frac{r}{100}\right)}^5$ (nghìn người).

b) Với r = 1,5, suy ra $\frac{r}{100}=\frac{\mathrm{1,5}}{100}=\mathrm{0,015}$.

Ta có khai triển:

(1 + 0,015)⁵ 

= 1⁵ + 5 . 1⁴ . 0,015 + 10 . 1³ . (0,015)² + 10 . 1² . (0,015)³ + 5 . 1 . (0,015)⁴ + (0,015)⁵.

Do đó: (1 + 0,015)⁵ ≈ 1⁵ + 5 . 1⁴ . 0,015 = 1,075.

Số dân của tỉnh đó sau 5 năm nữa là:

P₅ = 800 . (1 + 0,015)⁵ ≈ 800 . 1,075 = 860 (nghìn người).

Vậy số dân của tỉnh đó sau 5 năm nữa khoảng 860 nghìn người.